- 2021-05-29 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级下册数学试题课件-4第十八章18平行四边形的判定(二)
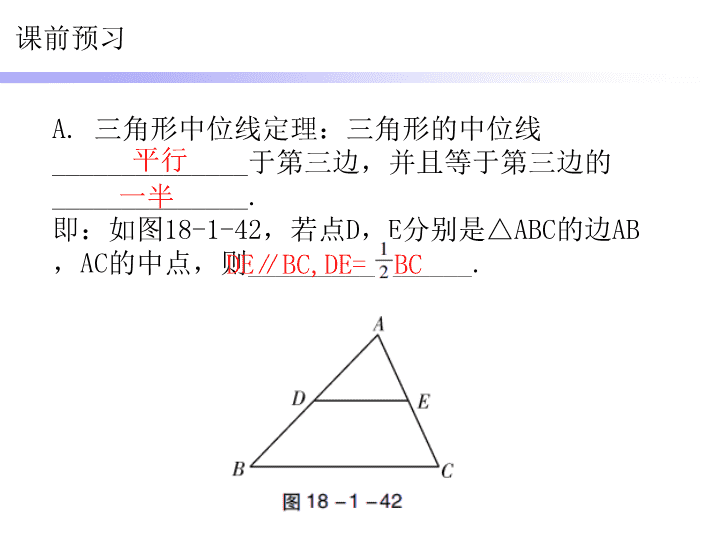
中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中 精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品 学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中 学精品教学资源 中 精品教学资源 中小学精品教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 精 品 教 学 资 源 中小学精品教 资源 中 小 学 精 品 教 学 资 源中小学精品教 资源 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精 教学资中小学精品教学资 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学 品教学资源 中小 精品教学资源 中小 精品教 资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品 资源 中小学精品教学 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 小学精品教 资源 中小学精品教 资源中小学精品教学资源 学精品教学资源 中 学精 教学资源 中 小 学 精 品 教 学 资 源 中 学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学 品教学资源中 精品教学资源 小 精品教学资源 中小学精品教学资源 中小学精品教学资源 中 学精品教学资 中小 精品教学资源 中小学精品教学资源 中小学精品 中小 精品教 资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 小 学 精 品 教 学 资 源 中小 精品 学资源 中 学精品教 资源中小 精品教学资源 中小学精品教学资源 中 学精品 资源 中 教学资源 中 精 教学资源 中小 品教学 源 中 小 学 精 品 教 学 资 源 小 学 精 品 教 学 资 源 中 小 学 品 教 资 源 中 小 学 品 教 资 源 中 小 品 教 资 源小学精品教 资 中 小 学 精 品 教 学 资 源中小学精品教 资 中 小 学 精 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 资 源 中 小 学 精 品 教 学 资 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 学 精 品 教 资 源 中 小 学 品 学 资 源 中 小 学 精 品 教 学 资 源 中 小 精 品 教 学 资 源 中小学精品教学资源 中小 精 教中小学精品教学 中小学精品教学资源 中小学 品教学资 中小 精品教学资源 中小 品教学资源 精品教学资源 第十八章 平行四边形 18.1 平行四边形 第4课时 平行四边形的判定(二) 课前预习 A. 三角形中位线定理:三角形的中位线 ______________于第三边,并且等于第三边的 ______________. 即:如图18-1-42,若点D,E分别是△ABC的边AB, AC的中点,则________________. 平行 一半 DE∥BC,DE= BC 1.如图18-1-43,在□ABCD中,AD=8,点E,F分别是BD, CD的中点,则EF=__________. 4 2. 如图18-1-44,在□ABCD中,AC,BD相交于点O,E 是AB的中点,∠BEO=120°,则∠BAD=__________. 3. 如图18-1-45,D,E,F分别为△ABC三边的中点, 则图中平行四边形有__________个. 120° 3 课堂讲练 【例】如图18-1-46,等边三角形ABC的边长是2,D,E 分别为AB,AC的中点,延长BC至点F,使CF= BC,连 接CD和EF. (1)求证:DE=CF;(2)求EF的长. 知识点 三角形中位线定理 (1)证明:∵D,E分别为AB,AC的中点, ∴DE∥BC且DE= BC. ∵CF= BC, ∴DE=CF. (2)解:由(1)得DE∥FC,DE=FC, ∴四边形DEFC是平行四边形.∴DC=EF. ∵D为AB的中点,等边三角形ABC的边长是2, ∴AD=BD=1,CD⊥AB,BC=2. ∴EF=DC= = . 1. 如图18-1-47,在△ABC中,M是BC的中点, AN平分∠BAC,AN⊥BN于N,延长BN交AC于点D, 已知AB=10,MN=4,BM=7,求△ABC的周长. 解:在△ANB和△AND中, ∠BAN=∠DAN, AN=AN, ∠ANB=∠AND=90°, ∴△ANB≌△AND(ASA). ∴AD=AB=10,BN=BD. ∵M是BC的中点,BN=BD, ∴BC=2BM=14,CD=2MN=8, ∴△ABC的周长=AB+BC+AC=10+14+8+10=42. 分层训练 【A组】 1. 如图18-1-48,在四边形ABCD中,对 角线AC,BD相交于点E,∠CBD=90°,BC =4,BE=ED=3,AC=10,则四边形ABCD 的面积为( ) A. 6 B. 12 C. 20 D. 24 D 2. 如图18-1-49,在四边形ABCD中,P是对角线BD 的中点,E,F分别是AB,CD的中点,AD=BC, ∠PEF=30°,则∠EPF的度数是( ) A. 120° B. 150° C. 135° D. 140° A 3. 如图18-1-50,AB是池塘两端,设计一方法测量 AB的距离,取点C,连接AC,BC,再取它们的中点D, E,测得DE=15 m,则AB=( ) A.7.5 m B.15 m C.22.5 m D.30 m D 4. 如图18-1-51,在Rt△ABC中,∠C=90°, AB=10,AC=6,D,E,F分别是△ABC三边的中点, 则△DEF的周长为( ) A. 24 B. 16 C. 14 D. 12 D 5. 如图18-1-52,在△ABC中,D,E分别是AB和AC的中 点,F是BC延长线上一点,CF=1,连接DF交CE于点G,且 EG=CG,则BC=__________. 6. 如图18-1-53,CD是△ABC的中线,点E,F分别是AC, DC的中点,EF=1,则BD=__________. 2 2 7. 如图18-1-54,在△ABC中,M,N分别是AB, AC的中点,且∠A+∠B=136°,则 ∠ANM=__________. 44° 8. 如图18-1-55,DE为△ABC的中位线,点F为 DE上一点,且∠AFB=90°,若AB=6,BC=8, 求EF的长. 解:∵DE为△ABC的中位 线, ∴DE= BC=4, ∵∠AFB=90°,D是AB的 中点, ∴DF= AB=3, ∴EF=DE-DF=1. 9. 如图18-1-56,AD,AE分别是△ABC的角平分 线和中线,CG⊥AD于点F,交AB于点G,若AB=8, AC=6,求EF的长. 【B组】 解:∵AD为△ABC的角平分线,CG⊥AD, ∴△ACG是等腰三角形. ∴AG=AC. ∵AC=6, ∴AG=AC=6,FG=CF. ∵AE为△ABC的中线, ∴EF是△BCG的中位线. ∴EF= BG. ∵AB=8, ∴BG=AB-AG=8-6=2. ∴EF=1. 10. 如图18-1-57,在△ABC中,AB=AC,CD是AB边上 的中线,延长AB到点E,使BE=AB,连接CE.求证: CD= CE. 证明:如答图18-1-5,作BF∥AC交EC于点F. ∵BF∥AC,∴∠FBC=∠ACB. ∵AB=AC,∴∠ABC=∠ACB. ∴∠FBC=∠ABC. ∵BF∥AC,BE=AB,∴BF= AC,CF= CE. ∵CD是AB边上的中线, ∴BD= AB. ∴BF=BD. 在△FBC和△DBC中, ∵BF=BD,∠FBC=∠DBC,BC=BC, ∴△FBC≌△DBC. ∴CD=CF. ∴CD= CE. 11. 如图18-1-58,点O是△ABC内一点,连接 OB,OC,线段AB,OB,OC,AC的中点分别为D, E,F,G. (1)判断四边形DEFG的形状,并说明理由; (2)若M为EF的中点,OM=2,∠OBC和∠OCB 互余,求线段BC的长. 解:(1)四边形DEFG是平行四边形, 理由如下:∵E,F分别为线段OB,OC的中点, ∴EF= BC,EF∥BC. 同理DG= BC,DG∥BC. ∴EF=DG,EF∥DG. ∴四边形DEFG是平行四边形. (2)∵∠OBC和∠OCB互余, ∴∠BOC=90°. ∵M为EF的中点,OM=2, ∴EF=2OM=4,∴BC=2EF=8. 12. 如图18-1-59,在△ABC中,AB=AC,点D, E分别是边AB,AC的中点,连接DE,BE,点F, G,H分别为BE,DE,BC的中点. (1)求证:FG=FH; (2)若∠A=90°,求证:FG⊥FH; (3)若∠A=80°,求∠GFH的度数. 【C组】 (1)证明:∵AB=AC,点D,E分别是边AB,AC 的中点,∴BD=EC. ∵点F,G,H分别为BE,DE,BC的中点, ∴FG∥BD,FG= BD,FH∥EC,FH= EC. ∴FG=FH. (2)证明:由(1)得FG∥BD. 又∵∠A=90°,∴FG⊥AC. ∵FH∥EC,∴FG⊥FH. (3)解:如答图18-1-6, 延长FG交AC于点K. ∵FG∥BD,∠A=80°, ∴∠FKC=∠A=80°. ∵FH∥EC, ∴∠GFH=180°-∠FKC=100°.查看更多