八年级下册数学教案 第二章复习 北师大版

八年级下册数学教案 第二章复习 北师大版

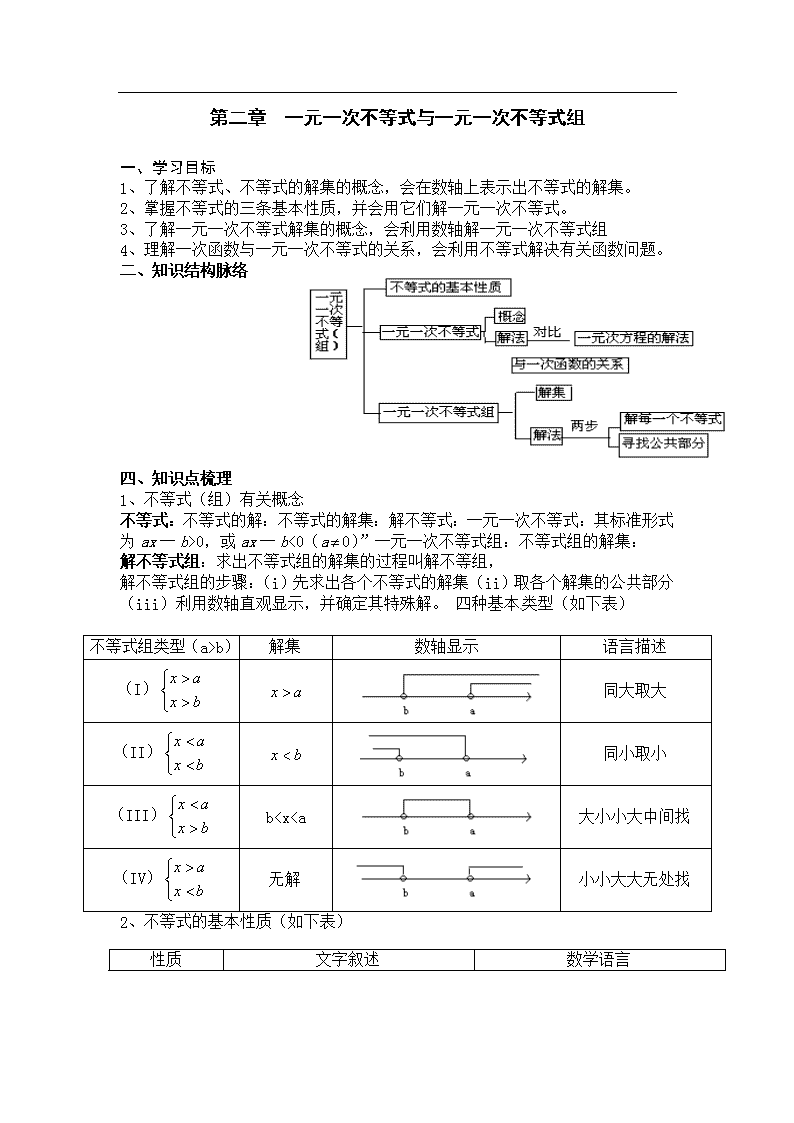
第二章　一元一次不等式与一元一次不等式组 ‎ ‎ 一、学习目标 1、 了解不等式、不等式的解集的概念，会在数轴上表示出不等式的解集。‎ 2、 掌握不等式的三条基本性质，并会用它们解一元一次不等式。‎ 3、 了解一元一次不等式解集的概念，会利用数轴解一元一次不等式组 4、 理解一次函数与一元一次不等式的关系，会利用不等式解决有关函数问题。‎ 二、知识结构脉络 ‎[来源:学+科+网Z+X+X+K]‎ 四、知识点梳理 1、 不等式（组）有关概念 不等式：不等式的解：不等式的解集：解不等式：一元一次不等式：其标准形式为ax一b>0，或ax一b<0（a0）”一元一次不等式组：不等式组的解集：‎ 解不等式组：求出不等式组的解集的过程叫解不等组，‎ 解不等式组的步骤：（i）先求出各个不等式的解集（ii）取各个解集的公共部分 ‎（iii）利用数轴直观显示，并确定其特殊解。 四种基本类型（如下表）‎ 不等式组类型（a>b）‎ 解集 数轴显示 语言描述 ‎（I）‎ 同大取大 ‎（II）‎ 同小取小 ‎（III）‎ bb则a土c>b土c ‎（II）‎ 不等式的两边乘以（或除以）同一个正数，不等号的方向不变 若a>b且c>0则ac>bc或 ‎（III）[来源:学,科,网]‎ 不等式的两边乘以（或除以）同一个负数，不等号的方向改变 若a>b且c<0则acb，c>d，则a十c>b十d（同向不等式相加）‎ （2） 若a>b，cb一d（异向不等式相减）‎ （3） 若a>b>0，c>d>0，ac>bd （4） 若a>b>0，0b>0，则 ‎（6） 若a>b>0，n为正整数，则 （7）若a>b>0，n为不小于2的整数则 ‎ ‎4、解不等式的步骤：（1）去分母（2）去括号（3）移项（4）合并同类项（5）未知数的系数化为1。要注意把系数化为1时，如果不等式的两边都乘以（或除以）同一个正数，不等号的方向不变；如果不等式的两边都乘以（或除以）同一个负数，不等号的方向要改变；解不等式要根据题目的要求和特点合理灵活地选择解题步骤。‎ ‎5、一元一次不等式（组）的应用 （1） 注意设未知数的方法，找出问题中量与量之间的不等关系，抽象出不等式（组），求出不等式（组）的解集后，要注意验证解的合理性。‎ （2） 正确理解列不等式（组）的关键词。如不少于、不超过、大于、小于、至少、至多、不足、不空、不满等。其中，不少于就是大于或等于表示为，不超过、至多都是不大于的意思，不大于就是小于或等于，表示为，非负数就是正数和零等。‎ 五、 思想方法总结 1. 应用类比的方法： ‎ ‎2.应用数形结合的思想：充分利用数轴的直观性，简捷性，生动形象地理解不等式和一次函授的有关知识，真正掌握基本技能。‎ ‎3.转化的思想方法：不等与相等之间可以相互转化，有时将不等问题转化为相等问题来解决，有时又可以将相等问题转化为不等问题来解决。‎ ‎4.构建的思想方法：列不等式（组）解决实际问题，实际上是应用构建的思想方法。所谓构建的思想方法是建立起解决实际问题的数学模型，如方程（组）、不等式（组）等，然后用数学模型解决实际问题，这种思想方法在今后应用广泛。‎ 六、 易错题分析 例1、若a>b，b，c为实数，则下列正确的是（）‎ A ac>bc， B acbc2 D ac2bc2[来源:Z。xx。k.Com]‎ 例2、关于x的不等式组无解，则m的取值范围（ ）‎ A m>3 B C D m<3[来源:Z#xx#k.Com]‎ 例3、x取何值时，x的一半与x的3倍的差至少是4？‎ 正解：由题意得即系数化为1，得故当时，x的一半与x的3倍的差至少是4。‎ 例4、（1）解不等式 ‎（2）解不等式并把解集在数轴上表示出来 例5、一辆公共汽车上有（5a一4）名乘客，在某一车站有（9一2a）名乘客下车，车上原来有多少名乘客？‎ 错解：由题意得解得 取整数得a=1,2,3,4‎ 把a的值分别代入5a一4，得5a一4=1，6，11，16。‎ 答：车上原来有1人，6人，11人，或16人。‎ 剖析：错解忽视了这一条件 正解：由题意得 化简得所以 a取整数得a=2，3，4‎ 当a=2时，5a一4=6，当a=3时，5a一4=11，当a=4时，5a一4=16。‎ 答：原来车上有乘客6人，11人，或16人。‎ 七、典型考点扫描 考点一：用不等式表示数量关系：‎ 图1‎ 例1、用不等式表示下列数量关系：‎ （1） x与3的和是非负数 （2） a与b的差是非正数 考点二：考查不等式（组）基础知识 例2：不等式的解集是（　　　　）‎ ‎　A、　　　　B、　　　C、　　　　D、‎ 例2:不等式≥3的解集在数轴上表示正确的是( )‎ 例3：如图1，小明和爸爸妈妈三人玩跷跷板．三人的体重一共为千克，爸爸坐在跷跷板的一端，体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端，这时爸爸那端仍然着地．那么小明的体重应小于（　　）‎ Ａ．千克 Ｂ．千克 Ｃ．千克 Ｄ．千克 例4关于x的不等式组只有4个整数解，则a的取值范围（ ）‎ A B C D 考点三、求不等式中字母的值 例4：如果关于的不等式（a+1）x＞a+1解集为x＜1，则a的取值范围是（ ）‎ A. a＞0 B.a＜0 C. a＞-1 D.a＜-1‎ 例5：关于x的不等式3x-2a≤-2的解集如图2,则a的值是______.‎ 考点四、考查一元一次不等式与一次函数 例6、己知当x取何值时？‎ 分析：方法一：可将函数或方程转化为不等式，即有求得自变量x的范图为x<一1。‎ 方法二：可作出两个函数的图象如图，所示：两直线相交于点（—1，3）依推上面的图象比下面的图象函数值大，求得自变量的范围。‎ 考点四、考查利用不等式（组）解实际应用问题 例7、(2006深圳市)初三的几位同学拍了一张合影作留念，已知冲一张底片需要0.80元，洗一张相片需要0.35元．在每位同学得到一张相片、共用一张底片的前提下，平均每人分摊的钱不足0.5元，那么参加合影的同学人数（ ）‎ Ａ．至多６人　　　Ｂ．至少６人　　　Ｃ．至多５人　　　Ｄ．至少５人 ‎ 例8:甲,乙两超市为了促销一种定价相同的商品,甲超市连续两次降价10%,乙超市一次降价20%,在哪家超市购买此种商品更合算(　　　)‎ A. 甲 　　B乙 　　C.同样 　　 D.与商品价格无关 例9:学校计划购买40支钢笔，若干本笔记本（笔记本数超过钢笔数）甲、乙两家文具店的标价都是钢笔10元/支，笔记本2元/支，甲店的优惠方式是钢笔打9折，笔记本打8折，乙店的优惠方式是每买5支送1本笔记本，钢笔不打折，购买的笔记本打7.5折，试问购买笔记本在什么范围内到甲店更合算？‎ 例10:“中国荷藕之乡”扬州市宝应县有着丰富的荷藕资源，某荷藕加工企业己收购荷藕60吨，根据市场信息，如果对荷藕进行粗加工，每天可 加工8吨，每吨可获利1000元，如果进行精加工，每天可加工0.5吨，每吨可获利5000元，由于受设备条件的限制，两种加工方式不能同时进行。‎ ‎（1）设精加工的吨数为x吨，则粗加工的吨数为 吨，加工这批荷藕需要 天，可获利 元（用含x的代数式表示）‎ ‎（2）为了保鲜的需要，该企业必须在一个月（30天）内将这批荷藕全部加工完毕。精加工的吨数在什么范围内，该企业加工这批荷藕的获利不低于80000元？‎ ‎[来源:学科网]‎ 一元一次不等式组解应用题的一般步骤为： 列不等式组解决实际问题的步骤与列一元一次不等式解应用题的步骤相类似,所不同的是,前者需寻求的不等关系往往不止一个,而后者只需找出一个不等关系即可。 1.审：认真审题，分清已知量、未知量及其关系，找出题中的不等关系，要抓住题中的关键词语，如“大于”、“小于”、“不大于”、“至少”、“不超过”、“超过”等； 2.设：设出适当的未知数； 3.列：根据题中的不等关系列出不等式组； 4.解：解出所列不等式组的解集； 5.答：写出答案，从不等式组的解集中找出符合题意的答