- 2021-05-29 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019高三数学(人教A版 文)一轮课时分层训练51 变量间的相关关系与统计案例
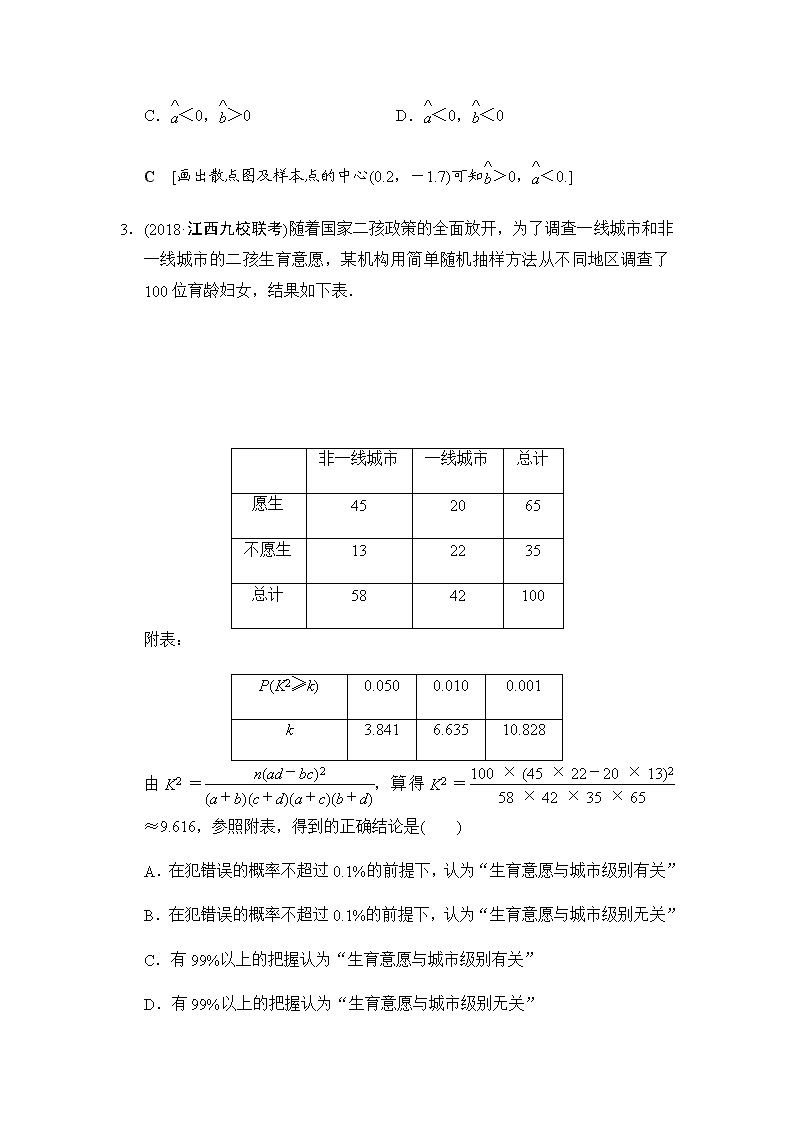
课时分层训练(五十一) 变量间的相关关系与统计案例 (对应学生用书第224页) A组 基础达标 (建议用时:30分钟) 一、选择题 1.已知变量x和y满足关系y=-0.1x+1,变量y与z正相关.下列结论中正确的是( ) 【导学号:79170339】 A.x与y正相关,x与z负相关 B.x与y正相关,x与z正相关 C.x与y负相关,x与z负相关 D.x与y负相关,x与z正相关 C [随着x的增大,y减小,z也减小,从而x与y负相关,x与z负相关.] 2.(2018·汉中模拟)已知两个随机变量x,y之间的相关关系如下表所示: x -4 -2 1 2 4 y -5 -3 -1 -0.5 1 根据上述数据得到的回归方程为=x+,则大致可以判断( ) A.>0,>0 B.>0,<0 C.<0,>0 D.<0,<0 C [画出散点图及样本点的中心(0.2,-1.7)可知>0,<0.] 3.(2018·江西九校联考)随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表. 非一线城市 一线城市 总计 愿生 45 20 65 不愿生 13 22 35 总计 58 42 100 附表: P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 由K2=,算得K2=≈9.616,参照附表,得到的正确结论是( ) A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关” B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关” C.有99%以上的把握认为“生育意愿与城市级别有关” D.有99%以上的把握认为“生育意愿与城市级别无关” C [∵K2=≈9.616>6.635, ∴有99%以上的把握认为“生育意愿与城市级别有关”,故选C.] 4.(2018·皖南模拟)下列说法错误的是( ) A.回归直线过样本点的中心(,) B.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近1 C.在回归直线方程=0.2x+0.8中,当解释变量x每增加1个单位时,预报 变量平均增加0.2个单位 D.对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关 系”的把握程度越小 D [对于A,回归直线过样本点的中心(,),正确; 对于B,两个随机变量相关性越强,则相关系数的绝对值越接近1,正确; 对于C,在线性回归方程=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量平均增加0.2个单位,正确; 对于D,对分类变量X与Y的随机变量K2的观测值k来说,k越大,“X与Y有关系”的把握程度越大,因此不正确.故选D.] 5.(2015·福建高考)为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x(万元) 8.2 8.6 10.0 11.3 11.9 支出y(万元) 6.2 7.5 8.0 8.5 9.8 根据上表可得回归直线方程=x+,其中=0.76,=- .据此估计,该社区一户年收入为15万元家庭的年支出为( ) 【导学号:79170340】 A.11.4万元 B.11.8万元 C.12.0万元 D.12.2万元 B [由题意知,==10, ==8, ∴=8-0.76×10=0.4, ∴当x=15时,=0.76×15+0.4=11.8(万元).] 二、填空题 6.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表: 理科 文科 总计 男 13 10 23 女 7 20 27 总计 20 30 50 已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025. 根据表中数据,得到K2=≈4.844. 则认为选修文科与性别有关系出错的可能性为________. 5% [∵K2≈4.844,根据假设检验的基本原理,应该断定“是否选修文科与性别之间有关系”成立,并且这种判断出错的可能性约为5%.] 7.(2018·唐山模拟)为了研究某种细菌在特定环境下随时间变化的繁殖规律,得到了下表中的实验数据,计算得回归直线方程为=0.85x-0.25.由以上信息,可得表中c的值为________. 天数x 3 4 5 6 7 繁殖数量y(千个) 2.5 3 4 4.5 c 6 [=(3+4+5+6+7)=5,=(2.5+3+4+4.5+c)=,代入回归直线方程得,=0.85×5-0.25,解得c=6.] 8.(2017·长沙雅礼中学质检)某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表: 气温(℃) 18 13 10 -1 用电量(度) 24 34 38 64 由表中数据得回归直线方程=x+中的=-2,预测当气温为-4 ℃时,用电量为________度. 68 [根据题意知==10,==40,因为回归直线过样本点的中心,所以=40-(-2)×10=60,所以当x=-4时,y=(-2)×(-4)+60=68,所以用电量为68度.] 三、解答题 9.(2017·石家庄质检) 微信是现代生活进行信息交流的重要工具,据统计,某公司200名员工中90%的人使用微信,其中每天使用微信时间在一小时以内的有60人,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中75%是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中是青年人. (1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出2×2列联表: 青年人 中年人 总计 经常使用微信 不经常使用微信 总计 (2)由列联表中所得数据判断,是否有99.9%的把握认为“经常使用微信与年龄有关”? 【导学号:79170341】 附:K2=. P(K2≥k0) 0.010 0.001 k0 6.635 10.828 [解] (1)由已知可得,该公司员工中使用微信的有200×90%=180(人), 经常使用微信的有180-60=120(人), 其中青年人有120×=80(人), 使用微信的人中青年人有180×75%=135(人), 所以2×2列联表: 青年人 中年人 总计 经常使用微信 80 40 120 不经常使用微信 55 5 60 总计 135 45 180 5分 (2)将列联表中数据代入公式可得: K2=≈13.333, 由于13.333>10.828,所以有99.9%的把握认为“经常使用微信与年龄有 关” . 12分 10.(2018·长沙模拟)已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图946所示: 图946 (1)试问这3年的前7个月中哪个月的月平均利润较高? (2)通过计算判断这3年的前7个月的总利润的发展趋势; (3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估计第3年8月份的利润. 月份 1 2 3 4 利润y(单位:百万元) 4 4 6 6 相关公式:==,=-. [解] (1)由折线图可知5月和6月的平均利润最高. 2分 (2)第1年前7个月的总利润为1+2+3+5+6+7+4=28(百万元), 3分 第2年前7个月的总利润为2+5+5+4+5+5+5=31(百万元), 4分 第3年前7个月的总利润为4+4+6+6+7+6+8=41(百万元), 5分 所以这3年的前7个月的总利润呈上升趋势. 6分 (3)∵=2.5,=5,x=12+22+32+42=30,xiyi=1×4+2×4+3×6+4×6=54, ∴==0.8,∴=5-2.5×0.8=3,∴=0.8x+3, 10分 当x=8时,=0.8×8+3=9.4. ∴估计第3年8月份的利润为9.4百万元. 12分 B组 能力提升 (建议用时:15分钟) 1.(2018·安阳模拟)已知变量x与y的取值如下表所示,且2.5<n<m<6.5,则由该数据算得的线性回归方程可能是( ) x 2 3 4 5 y 6.5 m n 2.5 A.=0.8x+2.3 B.=2x+0.4 C.=-1.5x+8 D.=-1.6x+10 D [由2.5<n<m<6.5,可得为负相关,排除A,B,由题意,知=3.5,=×(6.5+m+n+2.5)∈(3.5,5.5), 分别代入选项C,D,可得D满足.故选D.] 2.(2017·赣中南五校联考)心理学家分析发现视觉和空间想象能力与性别有关,某数学兴趣小组为了验证这个结论,从所在学校中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人) 几何题 代数题 总计 男同学 22 8 30 女同学 8 12 20 总计 30 20 50 根据上述数据,推断视觉和空间想象能力与性别有关系,则这种推断犯错误的概率不超过________. 附表: P(K2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 0.025 [由列联表计算K2的观测值 k=≈5.556>5.024, ∴推断犯错误的概率不超过0.025.] 3.(2018·汕头模拟)二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据: 使用年数x 2 3 4 5 6 7 售价y 20 12 8 6.4 4.4 3 z=ln y 3.00 2.48 2.08 1.86 1.48 1.10 下面是z关于x的折线图: 图947 (1)由折线图可以看出,可以用线性回归模型拟合z与x的关系,请用相关系数加以说明; (2)求y关于x的回归方程,并预测某辆A型号二手车当使用年数为9年时售价约为多少;(,小数点后保留两位有效数字) 【导学号:79170342】 (3)基于成本的考虑,该型号二手车的售价不得低于7 118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年. 参考公式:==,=-,r=. 参考数据: xiyi=187.4,xizi=47.64,x=139, =4.18, =13.96, =1.53,ln 1.46≈0.38,ln 0.711 8≈-0.34. [解] (1)由题意,知=×(2+3+4+5+6+7)=4.5,=×(3+2.48+2.08+1.86+1.48+1.10)=2, 又xizi=47.64, =4.18, =1.53, ∴r= =-≈-0.99, 3分 ∴z与x的相关系数大约为-0.99,说明z与x的线性相关程度很高.4分 (2)= =-≈-0.36, 5分 ∴=-=2+0.36×4.5=3.62, 6分 ∴z与x的线性回归方程是=-0.36x+3.62, 又z=ln y, ∴y关于x的回归方程是=e-0.36x+3.62. 令x=9, 8分 得=e-0.36×9+3.62=e0.38,∵ln 1.46≈0.38,∴=1.46, 即预测某辆A型号二手车当使用年数为9年时售价约为1.46万元.9分 (3)当≥0.711 8, 即e-0.36x+3.62≥0.711 8=eln 0.711 8=e-0.34时, 10分 则有-0.36x+3.62≥-0.34, 解得x≤11, 11分 因此,预测在收购该型号二手车时车辆的使用年数不得超过11年.12分查看更多