2017-2018学年贵州省遵义航天高级中学高二上学期第三次月考数学试题（理科）（解析版）

2017-2018学年贵州省遵义航天高级中学高二上学期第三次月考数学试题（理科）（解析版）

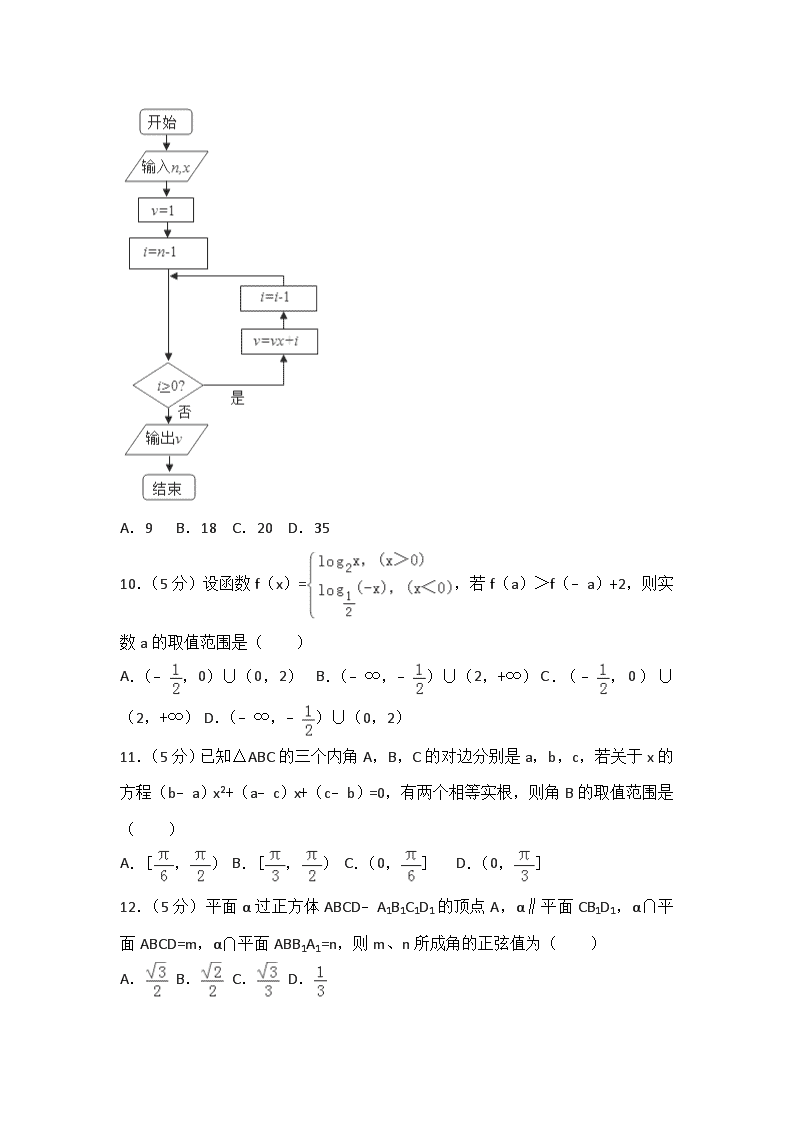
‎2017-2018学年贵州省遵义航天高级中学高二（上）第三次月考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）已知集合M={x|x2＜4}，N={x|（x﹣3）（x+1）＜0}，则集合M∩N=（　　）‎ A．{x|x＜﹣2} B．{x|x＞3} C．{x|﹣1＜x＜2} D．{x|2＜x＜3}‎ ‎2．（5分）下列函数中，在区间（0，+∞）上为增函数的是（　　）‎ A．y= B．y=（x﹣1）2 C．y=2﹣x D．y=log0.5（x+1）‎ ‎3．（5分）已知θ是第一象限的角，若sin4θ+cos4θ=，则sin2θ等于（　　）‎ A． B． C． D．‎ ‎4．（5分）已知等比数列{an}的公比为3，且a1+a3+a5=9，则（a5+a7+a9）=（　　）‎ A． B． C．6 D．﹣6‎ ‎5．（5分）下列命题中为真命题的是（　　）‎ A．若命题p：“∃x∈R，x2﹣x﹣1＞0，则命题p的否定为：“∀x∈R，x2﹣x﹣1≤0”‎ B．“a=1”是“直线x﹣ay=0与直线x+ay=0互相垂直”的充要条件 C．若x≠0，则x+≥2‎ D．直线a，b，为异面直线的充要条件是直线a，b不相交 ‎6．（5分）若将函数y=2sin2x的图象向左平移个单位长度，则平移后的图象的对称轴为（　　）‎ A．x=﹣（k∈Z） B．x=+（k∈Z） C．x=﹣（k∈Z） D．x=+（k∈Z）‎ ‎7．（5分）若x、y满足约束条件，若z=x+2y的最大值是6，则z的最小值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎8．（5分）一空间几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．2π+2 B．4π+2 C．2π+ D．4π+‎ ‎9．（5分）秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为（　　）‎ A．9 B．18 C．20 D．35‎ ‎10．（5分）设函数f（x）=，若f（a）＞f（﹣a）+2，则实数a的取值范围是（　　）‎ A．（﹣，0）∪（0，2） B．（﹣∞，﹣）∪（2，+∞） C．（﹣，0）∪（2，+∞） D．（﹣∞，﹣）∪（0，2）‎ ‎11．（5分）已知△ABC的三个内角A，B，C的对边分别是a，b，c，若关于x的方程（b﹣a）x2+（a﹣c）x+（c﹣b）=0，有两个相等实根，则角B的取值范围是（　　）‎ A．[，） B．[，） C．（0，] D．（0，]‎ ‎12．（5分）平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m、n所成角的正弦值为（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）向量，满足||=2，||=1，（+2）⊥（2﹣），则向量与的夹角为　 　．‎ ‎14．（5分）sin15°+sin75°的值是　 　．‎ ‎15．（5分）在[﹣1，1]上随机地取一个数k，则事件“直线y=kx与圆（x﹣5）2+y2=9相交”发生的概率为　 　．‎ ‎16．（5分）已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=4x，则f（﹣）+f（1）=　 　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（10分）数列{an}的前n项和记为Sn，a1=1，点（Sn，an+1）在直线y=3x+1上，n∈N*‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=log4an+1，cn=an+bn，Tn是数列{cn}的前n项和，求Tn．‎ ‎18．（12分）设．‎ ‎（I）求f（x）的单调减区间；‎ ‎（II）在锐角△ABC中，角A，B，C的对边分别为a，b，c．若，a=1，求△ABC面积的最大值．‎ ‎19．（12分）某校高二年级进行了百科知识大赛，为了了解高二年级900名同学的比赛情况，现在甲、乙两个班级各随机抽取了10名同学的成绩，比赛成绩满分为100分，80分以上可获得二等奖，90分以上可以获得一等奖，已知抽取的两个班学生的成绩（单位：分）数据的茎叶图如图1所示：‎ ‎（1）比较两组数据的分散程度（只需要给出结论），并求出甲组数据的频率分布直方图如图2中所示的a，b，c值；‎ ‎（2）现从两组数据中获奖的学生里分别随机抽取一人接受采访，求被周中的甲班学生成绩高于乙班学生成绩的概率．‎ ‎20．（12分）如图，在长方体ABCD﹣A1B1C1D1中，AA1=1，AB=AD=2，E、F分别是AB、BC的中点．‎ ‎（Ⅰ）证明A1、C1、F、E四点共面；‎ ‎（Ⅱ）求直线CD1与平面A1C1FE所成的角的正弦值．‎ ‎21．（12分）如图（1）所示，在直角梯形ABCD中，，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图（2）所示．‎ ‎（1）证明：CD⊥平面A1OC；‎ ‎（2）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD所成锐二面角的余弦值．‎ ‎22．（12分）在直角坐标系xOy中，以坐标原点O为圆心的圆与直线：x﹣y=4相切．‎ ‎（Ⅰ）求圆O的方程；‎ ‎（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|‎ 成等比数列，求•的取值范围．‎ ‎　‎ ‎2017-2018学年贵州省遵义航天高级中学高二（上）第三次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）已知集合M={x|x2＜4}，N={x|（x﹣3）（x+1）＜0}，则集合M∩N=（　　）‎ A．{x|x＜﹣2} B．{x|x＞3} C．{x|﹣1＜x＜2} D．{x|2＜x＜3}‎ ‎【分析】分别求出集合M，N，由此能求出集合M∩N．‎ ‎【解答】解：∵集合M={x|x2＜4}={x|﹣2＜x＜2}，‎ N={x|（x﹣3）（x+1）＜0}={x|﹣1＜x＜3}，‎ ‎∴集合M∩N={x|﹣1＜x＜2}．‎ 故选：C．‎ ‎【点评】本题考查交集的求法，是基础题，解题时时要认真审题，注意交集定义的合理运用．‎ ‎　‎ ‎2．（5分）下列函数中，在区间（0，+∞）上为增函数的是（　　）‎ A．y= B．y=（x﹣1）2 C．y=2﹣x D．y=log0.5（x+1）‎ ‎【分析】根据基本初等函数的单调性，判断各个选项中函数的单调性，从而得出结论．‎ ‎【解答】解：由于函数y=在（﹣1，+∞）上是增函数，故满足条件，‎ 由于函数y=（x﹣1）2在（0，1）上是减函数，故不满足条件，‎ 由于函数y=2﹣x在（0，+∞）上是减函数，故不满足条件，‎ 由于函数y=log0.5（x+1）在（﹣1，+∞）上是减函数，故不满足条件，‎ 故选：A．‎ ‎【点评】本题主要考查函数的单调性的定义和判断，基本初等函数的单调性，属于基础题．‎ ‎　‎ ‎3．（5分）已知θ是第一象限的角，若sin4θ+cos4θ=，则sin2θ等于（　　）‎ A． B． C． D．‎ ‎【分析】根据已知正弦和余弦的四次方和的值和要求的结论是sin2θ，所以把正弦和余弦的平方和等于1两边平方，又根据θ是第一象限的角，判断出要求结论的符号，得到结果．‎ ‎【解答】解：∵sin2θ+cos2θ=1，‎ ‎∴sin4θ+cos4θ+2sin2θcos2θ=1，‎ ‎∵sin4θ+cos4θ=，‎ ‎∴2sin2θcos2θ=，‎ ‎∵θ是第一象限的角，‎ ‎∴sin2θ=，‎ 故选：C．‎ ‎【点评】已知一个角的某个三角函数式的值，求这个角的其他三角函数式的值，一般需用三个基本关系式及其变式，通过恒等变形或解方程求解．‎ ‎　‎ ‎4．（5分）已知等比数列{an}的公比为3，且a1+a3+a5=9，则（a5+a7+a9）=（　　）‎ A． B． C．6 D．﹣6‎ ‎【分析】根据等比数列的性质结合对数的运算法则进行求解即可．‎ ‎【解答】解：∵等比数列{an}的公比为3，且a1+a3+a5=9，‎ ‎∴a5+a7+a9=（a1+a3+a5）q4=9×34=36，‎ 则（a5+a7+a9）=36=﹣log336=﹣6，‎ 故选：D．‎ ‎【点评】本题主要考查对数值的计算，根据等比数列的性质结合对数的运算法则是解决本题的关键．‎ ‎　‎ ‎5．（5分）下列命题中为真命题的是（　　）‎ A．若命题p：“∃x∈R，x2﹣x﹣1＞0，则命题p的否定为：“∀x∈R，x2﹣x﹣1≤0”‎ B．“a=1”是“直线x﹣ay=0与直线x+ay=0互相垂直”的充要条件 C．若x≠0，则x+≥2‎ D．直线a，b，为异面直线的充要条件是直线a，b不相交 ‎【分析】逐一分析四个答案的真假，可得结论．‎ ‎【解答】解：若命题p：“∃x∈R，x2﹣x﹣1＞0，则命题p的否定为：“∀x∈R，x2﹣x﹣1≤0”，故A是真命题；‎ ‎“直线x﹣ay=0与直线x+ay=0互相垂直”⇔“a=±1”，故“a=1”是“直线x﹣ay=0与直线x+ay=0互相垂直”的充分不必要条件，故B为假命题；‎ 若x＞0，则x+≥2，或若x＜0，则x+≤﹣2，故C为假命题．‎ 直线a，b，为异面直线的充要条件是直线a，b不相交且不平行，‎ 故选A ‎【点评】本题考查的知识点是命题的真假判断与应用，难度中档．‎ ‎　‎ ‎6．（5分）若将函数y=2sin2x的图象向左平移个单位长度，则平移后的图象的对称轴为（　　）‎ A．x=﹣（k∈Z） B．x=+（k∈Z） C．x=﹣（k∈Z） D．x=+（k∈Z）‎ ‎【分析】利用函数y=Asin（ωx+φ）（A＞0，ω＞0）的图象的变换及正弦函数的对称性可得答案．‎ ‎【解答】解：将函数y=2sin2x的图象向左平移个单位长度，得到y=2sin2（x+）=2sin（2x+），‎ 由2x+=kπ+（k∈Z）得：x=+（k∈Z），‎ 即平移后的图象的对称轴方程为x=+（k∈Z），‎ 故选：B．‎ ‎【点评】本题考查函数y=Asin（ωx+φ）（A＞0，ω＞0）的图象的变换规律的应用及正弦函数的对称性质，属于中档题．‎ ‎　‎ ‎7．（5分）若x、y满足约束条件，若z=x+2y的最大值是6，则z的最小值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【分析】本题考查的知识点是简单的线性规划，我们可以先画出足约束条件的平面区域，再根据目标函数z=x+2y的最大值是6，求出点的横坐标即可．‎ ‎【解答】解：满足约束条件的平面区域如下图：‎ ‎∵目标函数z=x+2y的最大值是6，‎ 可得，可得A（2，2）．‎ ‎∴当x=2，y=2时，Z取最大值6，‎ A（2，2）在直线x=a上，可得a=2，‎ 故选：A．‎ ‎【点评】用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．‎ ‎　‎ ‎8．（5分）一空间几何体的三视图如图所示，则该几何体的体积为（　　）‎ A．2π+2 B．4π+2 C．2π+ D．4π+‎ ‎【分析】由三视图及题设条件知，此几何体为一个上部是四棱锥，下部是圆柱其高已知，底面是半径为1的圆，故分别求出两个几何体的体积，再相加即得组合体的体积．‎ ‎【解答】解：此几何体为一个上部是正四棱锥，下部是圆柱 由于圆柱的底面半径为1，其高为2，故其体积为π×12×2=2π 棱锥底面是对角线为2的正方形，故其边长为，其底面积为2，又母线长为2，‎ 故其高为 由此知其体积为=‎ 故组合体的体积为2π+‎ 故选C ‎【点评】‎ 本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是组合体的体积，其方法是分部来求，再求总体积．三视图的投影规则是：“主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等”．三视图是高考的新增考点，不时出现在高考试题中，应予以重视．‎ ‎　‎ ‎9．（5分）秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为（　　）‎ A．9 B．18 C．20 D．35‎ ‎【分析】由题意，模拟程序的运行，依次写出每次循环得到的i，v的值，当i=﹣1时，不满足条件i≥0，跳出循环，输出v的值为18．‎ ‎【解答】解：初始值n=3，x=2，程序运行过程如下表所示：‎ v=1‎ i=2 v=1×2+2=4‎ i=1 v=4×2+1=9‎ i=0 v=9×2+0=18‎ i=﹣1 跳出循环，输出v的值为18．‎ 故选：B．‎ ‎【点评】本题主要考查了循环结构的程序框图的应用，正确依次写出每次循环得到的i，v的值是解题的关键，属于基础题．‎ ‎　‎ ‎10．（5分）设函数f（x）=，若f（a）＞f（﹣a）+2，则实数a的取值范围是（　　）‎ A．（﹣，0）∪（0，2） B．（﹣∞，﹣）∪（2，+∞） C．（﹣，0）∪（2，+∞） D．（﹣∞，﹣）∪（0，2）‎ ‎【分析】根据已知中函数f（x）=，结合对数的运算性质，分类讨论满足f（a）＞f（﹣a）+2的a值范围，综合可得答案．‎ ‎【解答】解：若a＞0，则f（a）＞f（﹣a）+2可化为：，‎ 即log2a＞1，‎ 解得：a＞2，‎ 若a＜0，则f（a）＞f（﹣a）+2可化为：，‎ 即，‎ 解得：＜a＜0，‎ 综上实数a的取值范围是（﹣，0）∪（2，+∞），‎ 故选：C ‎【点评】本题考查的知识点是分段函数的应用，对数函数的图象和性质，难度中档．‎ ‎　‎ ‎11．（5分）已知△ABC的三个内角A，B，C的对边分别是a，b，c，若关于x的方程（b﹣a）x2+（a﹣c）x+（c﹣b）=0，有两个相等实根，则角B的取值范围是（　　）‎ A．[，） B．[，） C．（0，] D．（0，]‎ ‎【分析】利用判别式等于0，可得a+c=2b，利用余弦定理，结合基本不等式，即可求出角B的取值范围．‎ ‎【解答】解：∵方程（b﹣a）x2+（a﹣c）x+（c﹣b）=0，有两个相等实根，‎ ‎∴△=（a﹣c）2﹣4（b﹣a）（c﹣b）=0，‎ ‎∴（a+c）2﹣4b（a+c）+4b2=0‎ ‎∴（a+c﹣2b）2=0‎ ‎∴a+c=2b，‎ cosB===﹣≥，‎ ‎∴B是△ABC的内角，‎ ‎∴0＜B≤．‎ 故选：D．‎ ‎【点评】本题考查余弦定理，基本不等式，考查学生分析解决问题的能力，属于中档题．‎ ‎　‎ ‎12．（5分）平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m、n所成角的正弦值为（　　）‎ A． B． C． D．‎ ‎【分析】画出图形，判断出m、n所成角，求解即可．‎ ‎【解答】解：如图：α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABA1B1=n，‎ 可知：n∥CD1，m∥B1D1，∵△CB1D1是正三角形．m、n所成角就是∠‎ CD1B1=60°．‎ 则m、n所成角的正弦值为：．‎ 故选：A．‎ ‎【点评】本题考查异面直线所成角的求法，考查空间想象能力以及计算能力．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）向量，满足||=2，||=1，（+2）⊥（2﹣），则向量与的夹角为　π　．‎ ‎【分析】根据向量垂直得（+2）•（2﹣）=0，展开计算可求出，代入数量积公式即可求出夹角．‎ ‎【解答】解：∵（+2）⊥（2﹣），‎ ‎∴（+2）•（2﹣）=2+3﹣2=0，‎ 即8+3﹣2=0，∴=﹣2．‎ ‎∴cos＜＞==﹣1．‎ ‎∴＜＞=π．‎ 故答案为：π．‎ ‎【点评】本题考查了平面向量的数量积运算，属于中档题．‎ ‎　‎ ‎14．（5分）sin15°+sin75°的值是　　．‎ ‎【分析】利用诱导公式以及两角和的正弦函数化简求解即可．‎ ‎【解答】解：sin15°+sin75°=sin15°+cos15°=（sin15°cos45°+cos15°sin45°）=sin60°=．‎ 故答案为：．‎ ‎【点评】本题考查两角和的正弦函数，三角函数的化简求值，考查计算能力．‎ ‎　‎ ‎15．（5分）在[﹣1，1]上随机地取一个数k，则事件“直线y=kx与圆（x﹣5）2+y2=9相交”发生的概率为　　．‎ ‎【分析】利用圆心到直线的距离小于半径可得到直线与圆相交，可求出满足条件的k，最后根据几何概型的概率公式可求出所求．‎ ‎【解答】解：圆（x﹣5）2+y2=9的圆心为（5，0），半径为3．‎ 圆心到直线y=kx的距离为，‎ 要使直线y=kx与圆（x﹣5）2+y2=9相交，则＜3，解得﹣＜k＜．‎ ‎∴在区间[﹣1，1]上随机取一个数k，使直线y=kx与圆（x﹣5）2+y2=9相交相交的概率为=．‎ 故答案为：．‎ ‎【点评】本题主要考查了几何概型的概率，以及直线与圆相交的性质，解题的关键弄清概率类型，同时考查了计算能力，属于基础题．‎ ‎　‎ ‎16．（5分）已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=4x，则f（﹣）+f（1）=　﹣2　．‎ ‎【分析】‎ 根据题意，由函数的周期性与奇偶性可得f（﹣1）=f（1）且f（﹣1）=﹣f（1），分析可得f（1）的值，进而分析可得f（﹣）=﹣f（）=﹣f（），由函数的解析式计算可得答案．‎ ‎【解答】解：根据题意，函数f（x）是定义在R上的周期为2的奇函数，‎ 则有f（﹣1）=f（1）且f（﹣1）=﹣f（1），‎ 即f（1）=﹣f（1），则f（1）=0，‎ f（﹣）=﹣f（）=﹣f（）=﹣（）=﹣2，‎ 则f（﹣）+f（1）=﹣2+0=﹣2；‎ 故答案为：﹣2．‎ ‎【点评】本题考查函数的奇偶性与周期性，注意求出f（1）的值．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（10分）数列{an}的前n项和记为Sn，a1=1，点（Sn，an+1）在直线y=3x+1上，n∈N*‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）设bn=log4an+1，cn=an+bn，Tn是数列{cn}的前n项和，求Tn．‎ ‎【分析】（I）根据递推公式可得{an}为等比数列，从而得出通项公式；‎ ‎（II）求出bn，利用分项求和得出Tn．‎ ‎【解答】解：（I）由题意得an+1=3Sn+1，∴an=3Sn﹣1+1（n≥2），‎ 两式相减得an+1﹣an=3an（n≥2），即an+1=4an，‎ 又a2=3a1+1=4=4a1，‎ ‎∴{an}是以1为首项，4为公比的等比数列．‎ ‎∴．‎ ‎（II），∴，‎ ‎∴．‎ ‎【点评】本题考查了等比关系的确定，等差数列，等比数列的求和公式，属于中档题．‎ ‎　‎ ‎18．（12分）设．‎ ‎（I）求f（x）的单调减区间；‎ ‎（II）在锐角△ABC中，角A，B，C的对边分别为a，b，c．若，a=1，求△ABC面积的最大值．‎ ‎【分析】（Ⅰ）首先利用三角函数关系式的恒等变换，把函数关系式变形成正弦型函数，进一步求出函数的单调递减区间．‎ ‎（Ⅱ）首先利用锐角三角形求出A的值，进一步利用余弦定理和基本不等式求出bc的最大值，最后求出三角形面积的最大值．‎ ‎【解答】解：（Ⅰ）f（x）=sinxcosx﹣，‎ ‎=，‎ ‎=．‎ 令：（k∈Z），‎ 解得：（k∈Z），‎ 所以函数的单调递减区间为：（k∈Z）．‎ ‎（Ⅱ）在锐角△ABC中，角A，B，C的对边分别为a，b，c．若，a=1，‎ 所以：sinA=，‎ A=，‎ 由余弦定理得：a2=b2+c2﹣2bccosA，‎ 由于b2+c2≥2bc，‎ ‎．‎ 所以：，‎ 即面积的最大值为：．‎ ‎【点评】本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数单调性的应用，余弦定理的应用，三角形面积公式的应用．属于基础题型．‎ ‎　‎ ‎19．（12分）某校高二年级进行了百科知识大赛，为了了解高二年级900名同学的比赛情况，现在甲、乙两个班级各随机抽取了10名同学的成绩，比赛成绩满分为100分，80分以上可获得二等奖，90分以上可以获得一等奖，已知抽取的两个班学生的成绩（单位：分）数据的茎叶图如图1所示：‎ ‎（1）比较两组数据的分散程度（只需要给出结论），并求出甲组数据的频率分布直方图如图2中所示的a，b，c值；‎ ‎（2）现从两组数据中获奖的学生里分别随机抽取一人接受采访，求被周中的甲班学生成绩高于乙班学生成绩的概率．‎ ‎【分析】（1）由茎叶图中数据分布情况，得出甲、乙两组数据分散程度；根据频率分布直方图计算a、b、c的值；‎ ‎（ II）由茎叶图知甲、乙两班获奖人数，计算所求的概率值．‎ ‎【解答】解：（1）由茎叶图可知，甲组数据成单峰分布，更集中些，‎ 乙组数据不成单峰分布，更分散些；‎ 根据频率分布直方图知，‎ a==0.05，‎ b==0.02，‎ c==0.01；‎ ‎（ II）由茎叶图知：甲班获奖4人，乙班获奖5人，‎ 所以甲班学生成绩高于乙班学生成绩的概率为：‎ ‎．‎ ‎【点评】本题考查了茎叶图与频率分布直方图的应用问题，也考查了古典概型的概率计算问题，是基础题．‎ ‎　‎ ‎20．（12分）如图，在长方体ABCD﹣A1B1C1D1中，AA1=1，AB=AD=2，E、F分别是AB、BC的中点．‎ ‎（Ⅰ）证明A1、C1、F、E四点共面；‎ ‎（Ⅱ）求直线CD1与平面A1C1FE所成的角的正弦值．‎ ‎【分析】（Ⅰ）连接AC，证明EF∥AC，推出EF∥A1C1，即可证明A1、C1、F、E四点共面．‎ ‎（Ⅱ）以D为坐标原点，DA、DC、DD1分别为xyz轴，建立空间直角坐标系，易求得，求出平面A1C1EF的法向量，利用空间向量的数量积求解直线CD1与平面A1C1FE所成的角的正弦函数值即可．‎ ‎【解答】解：（Ⅰ）连接AC，因为E，F分别是AB，BC的中点，‎ 所以EF是△ABC的中位线，‎ 所以EF∥AC．由长方体的性质知AC∥A1C1，‎ 所以EF∥A1C1，‎ 所以A1、C1、F、E四点共面．‎ ‎（Ⅱ）以D为坐标原点，DA、DC、DD1分别为xyz轴，建立空间直角坐标系，易求得，‎ 设平面A1C1EF的法向量为 则，即，z=1，得x=1，y=1，所以，‎ 所以=，‎ 所以直线CD1与平面A1C1FE所成的角的正弦函数值为：．‎ ‎【点评】本题考查直线与平面所成角的求法，空间四点共面，平面的基本性质的应用，考查空间想象能力计算能力以及逻辑推理能力．‎ ‎　‎ ‎21．（12分）如图（1）所示，在直角梯形ABCD中，，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图（2）所示．‎ ‎（1）证明：CD⊥平面A1OC；‎ ‎（2）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD所成锐二面角的余弦值．‎ ‎【分析】（1）BE⊥平面A1OC，又BE∥CD，即可证明：CD⊥平面A1OC；‎ ‎（2）若平面A1BE⊥平面BCDE，以O为原点，OB，OC，OA1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，求出平面的法向量，即可求平面A1BC与平面A1CD所成锐二面角的余弦值．‎ ‎【解答】（1）证明：在图（1）中，因为，E是AD的中点，且，‎ 所以BE⊥AC，BE∥CD，‎ 即在图（2）中，BE⊥OA1，BE⊥OC，又OA1∩OC=O，OA1⊂平面A1OC，OC⊂平面A1OC，‎ 从而BE⊥平面A1OC，又BE∥CD，所以CD⊥平面A1OC．‎ ‎（2）解：由已知，平面A1BE⊥平面BCDE，且交线为BE，‎ 又由（1）知，BE⊥OA1，所以OA1⊥平面BCDE，‎ 如图，以O为原点，OB，OC，OA1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，‎ 设，所以，‎ 得．‎ 设平面A1BC的法向量，平面A1CD的法向量，‎ 平面A1BC与平面A1CD的夹角为θ，‎ 则得，取，同理，取，‎ 从而，‎ 即平面A1BC与平面A1CD所成锐二面角的余弦值为．‎ ‎【点评】本题考查线面垂直的判定，考查平面A1BC与平面A1CD所成锐二面角的余弦值，考查学生向量知识的运用，属于中档题．‎ ‎　‎ ‎22．（12分）在直角坐标系xOy中，以坐标原点O为圆心的圆与直线：x﹣y=4相切．‎ ‎（Ⅰ）求圆O的方程；‎ ‎（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求•的取值范围．‎ ‎【分析】（Ⅰ）圆的半径为圆心到切线的距离r==2，从而写出圆O的方程；‎ ‎（Ⅱ）设P（x，y），从而由|PA|•|PB|=|PO|2得x2=y2+2，由点P在圆内可得x2+y2＜4，从而可得0≤y2＜1，•=（﹣2﹣x，﹣y）•（2﹣x，﹣y）=x2+y2﹣4，从而解得．‎ ‎【解答】解：（Ⅰ）∵以坐标原点O为圆心的圆与直线：x﹣y=4相切，‎ ‎∴r==2，O（0，0），‎ ‎∴圆O的方程为 x2+y2=4；‎ ‎（Ⅱ）圆O与x轴相交于A（﹣2，0）、B（2，0）两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，‎ ‎∴|PA|•|PB|=|PO|2，设点P（x，y），．‎ 则有 =x2+y2，‎ 即x2=y2+2．‎ 由点P在圆内可得 x2+y2＜4，故有 0≤y2＜1；‎ ‎∵•=（﹣2﹣x，﹣y）•（2﹣x，﹣y）=x2+y2﹣4=2（y2﹣1）∈[﹣2，0）．‎ 即•的取值范围是[﹣2，0）．‎ ‎【点评】本题考查了圆的方程的应用及向量的数量积的求法．‎ ‎　‎