第5章位置的确定复习教案

第5章位置的确定复习教案

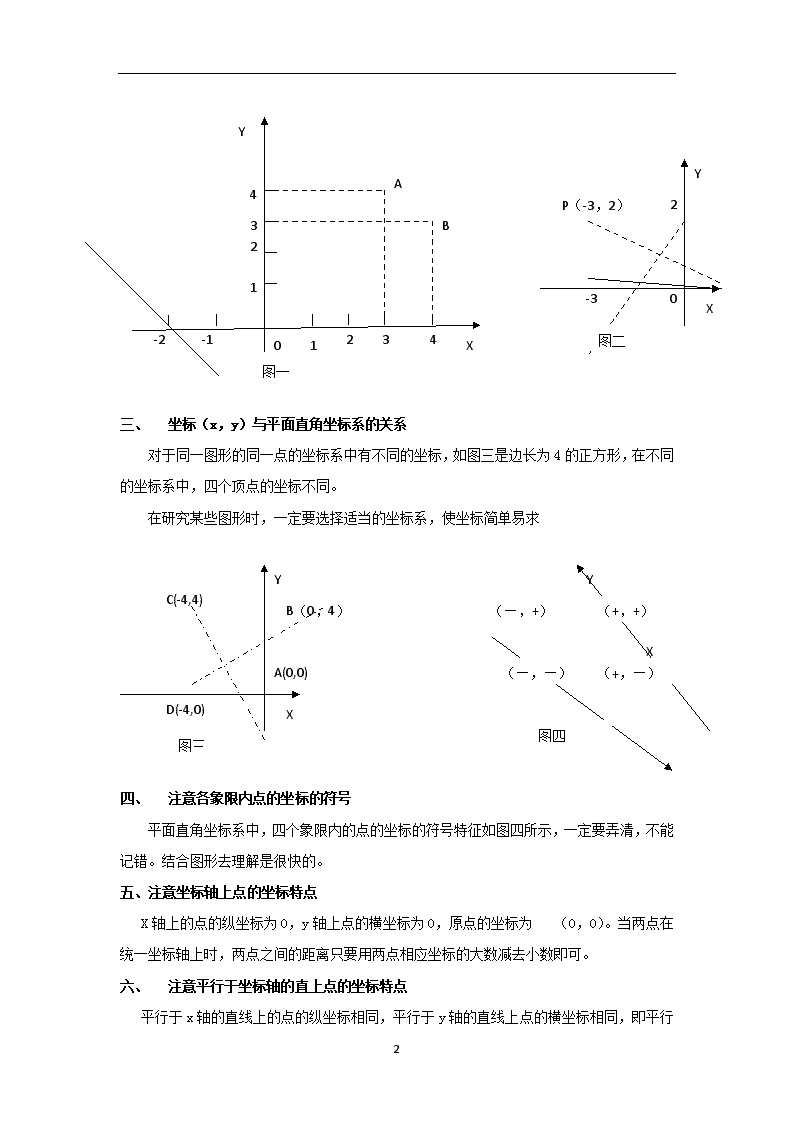
‎ ‎ 第五章《位置的确定》复习教案 复习内容：‎ 通过确定位置、平面直角坐标系、变化的鱼这三节内容的学习，让学生通过感受实例，了解物体位置的确定有多种方式和方法，能灵活的选择合适的方法来表示物体的位置；通过联想模仿初步体会平面指标坐标系建立的方法，理解直角坐标系的概念，并能在给定的直角坐标系内，根据坐标描述点的位置，或根据点的位置写出它的坐标；能在方格纸上建立适当的直角坐标系来描述物体的位置，能知道一些特殊点坐标的特征，能根据这些特征求一些特殊点的坐标；通过画图让学生体会点的坐标的变化引起的图的变化，或图形变化后点的坐标变化之间的关系，培养学生数形结合的意识、形象思维能力和数学应用能力，形成良好的数学观。这一章作为图形与坐标的主体内容，它是空间与图形的四个重要组成部分之一，也是本册书中一次函数的重要基础，它从坐标的角度使学生进一步体会图形平移，轴对称的数学内涵，是一章体现数形结合思想很好的内容。学好本章内容，我认为关键要掌握平面直角坐标系中点坐标的一些要点，叙述如下：‎ 掌握坐标的八个要点 要学好平面直角坐标系应注意以下几点：‎ 一、 坐标（x，y）与点的对应关系 坐标（x，y）与坐标系上的点是一一对应的，在坐标（x，y）中，x与y的顺序不能颠倒，如图一中，点A（3，4）与点B（4，3）是表示不同的点。‎ 点的坐标要用两个数表示，当点在坐标轴上时，有一个坐标为0，不能省略不写，如图中点C（-2，0）不能写成C（-2）‎ 二、 坐标（x，y）的几何意义 平面直角坐标系是代数与几何联系的纽带，坐标（x，y）有某几何意义，如图二中P（-3，2）它到x轴、y轴的距离分别是︱2︱=2， ︱3︱=3。学生不理解这个几何意义，很容易出错。‎ 3‎ ‎ ‎ Y X 图二 P（-3，2）‎ ‎2‎ ‎0‎ ‎-3‎ B A ‎0‎ Y ‎-1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ X ‎-2‎ 图一 一、 坐标（x，y）与平面直角坐标系的关系 对于同一图形的同一点的坐标系中有不同的坐标，如图三是边长为4的正方形，在不同的坐标系中，四个顶点的坐标不同。‎ 在研究某些图形时，一定要选择适当的坐标系，使坐标简单易求 ‎（+，+）‎ ‎（—，+）‎ Y C(-4,4)‎ Y X 图四 ‎（+，—）‎ ‎（—，—）‎ X 图三 D(-4,0)‎ B（0，4）‎ A(0,0)‎ 二、 注意各象限内点的坐标的符号 平面直角坐标系中，四个象限内的点的坐标的符号特征如图四所示，一定要弄清，不能记错。结合图形去理解是很快的。‎ 五、注意坐标轴上点的坐标特点 X轴上的点的纵坐标为0，y轴上点的横坐标为0，原点的坐标为 （0，0）。当两点在统一坐标轴上时，两点之间的距离只要用两点相应坐标的大数减去小数即可。‎ 六、 注意平行于坐标轴的直上点的坐标特点 3‎ ‎ ‎ 平行于x轴的直线上的点的纵坐标相同，平行于y轴的直线上点的横坐标相同，即平行与x轴的直线上的两点为（X1,a），（X2,a）；平行于y轴的直线上的两点为（a，Y1）,（a，Y2）.‎ 六、 注意关于坐标轴及原点对称的点的坐标特征 ‎ 点P(x,y)关于x轴对称的点P1的坐标是P(x,-y)；关于y轴对称的点P2的坐标是(-x,y)，关于原点对称的点P3的坐标是(-x,-y)。‎ 七、 注意平面直角坐标系中点（图形）的平移规律 在平面直角坐标系中，将点(x,y)向右（或左）平移a个单位长度，可以得到对应点(x+a,y)【或(x-a,y)】；将点(x,y)向上或向下平移b个单位长度，可以得到对应点(x,y+b)或 (x,y-b)。‎ 同样，在直角平面坐标系中，如果把一个图形上各个点的横坐标都加上（或减去）一个正数a，相应的新图形就是把原图形向右（或向左）平移a个单位长度，如果把它的各个点的纵坐标都加上（或减去）一个正数a，相应的新图形就是把原图形向上（或向下）平移a个单位长度。‎ 掌握好以上内容，才能更好的为后面章节的学习打好基础。‎ 因为本章有很多图形，用计算机动态演示，可以帮助学生更好的理解图形与坐标之间的关系，但有时介于条件的限制，不能利用计算机上课，此时只能使用课本，能否将本章的例题真正设置成学案形式，即只有例题，不设置答案，便于教师更好的利用教材。‎ 3‎