北师大版数学九年级上册同步课件-2第二章-2应用一元二次方程

北师大版数学九年级上册同步课件-2第二章-2应用一元二次方程

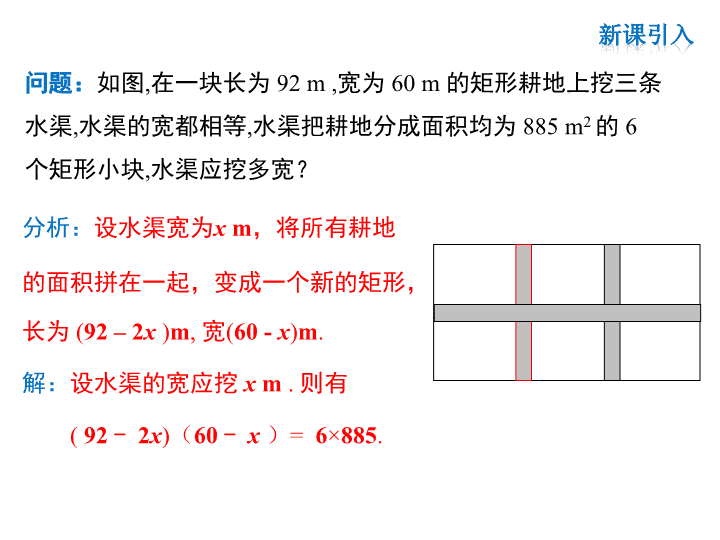
第二章 一元二次方程 2.6 应用一元二次方程 第1课时 行程问题及几何问题 学习目标 1.掌握列一元二次方程解决几何问题、数学问题,并能根据具体 问题的实际意义,检验结果的合理性.（重点、难点） 2.理解将实际问题抽象为方程模型的过程,并能运用所学的知识 解决问题． 问题：如图,在一块长为 92 m ,宽为 60 m 的矩形耕地上挖三条 水渠,水渠的宽都相等,水渠把耕地分成面积均为 885 m2 的 6 个 矩形小块,水渠应挖多宽？ 分析：设水渠宽为x m，将所有耕地 的面积拼在一起，变成一个新的矩形， 长为 (92 – 2x )m, 宽(60 - x)m. 解：设水渠的宽应挖 x m . 则有 ( 92 - 2x)（60 - x ）= 6×885. 如图,某海军基地位于A处,在其正南方向200 n mile 处有一 重要目标B,在B的正东方向200 n mile 处有一重要目标C.小岛 D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一 艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发, 沿南偏西方向匀速直线航行,欲将一批物品送达军舰. 已知军舰的速度是补给船的2倍,军舰在 由B到C的途中与补给船相遇于E处,那么 相遇时补给船航行了多少海里(结果精确 到0.1海里)？ 东 北A B C D F 利用一元二次方程解决行程（几何）问题1 例1 东 北 A B C D FE 设相遇时补给船航行了x n mile,那么 DE = x n mile , AB+ BE = 2x n mile, EF = AB + BF - (AB + BE) = (300 - 2x)n mile. 在Rt△DEF中，根据勾股定理可得方程 x2 = 1002 + (300 - 2x)2. 整理，得 3x2 - 1200x + 100 000 = 0 , 解得 (不合题意，舍去) 3 61002004118 3 6100200 21  xx ,. 解：连结DF.∵AD=CD , BF=CF,∴DF是△ABC的中位线. ∴DF∥AB，且DF= AB. ∵AB⊥BC, AB = BC =200 n mile, ∴DF⊥BC, DF =100 n mile，BF=100 n mile. 1 2 《九章算术》“勾股”章中有一题:“今有二人同所立. 甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会. 问甲、乙各行几何?” 大意是说:已知甲、乙二人同时从同一地点出发,甲的速度是7,乙 的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向 走了一段后与乙相遇.那么相遇时,甲、乙各走了多远? 解:设甲、乙相遇时所用时间为x. 根据题意,得 (7x - 10)2 = (3x) 2 +10 2. 整理,得 2x2 - 7x = 0. 解方程,得 x1=3.5, x2=0 (不合题意,舍去). ∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5. 答:甲走了24.5步,乙走了10.5步. 乙:3x 甲: 10 A B C 7x-10 例2 一块长和宽分别为60 cm 和40 cm 的长方形铁皮,要在它的 四角截去四个相等的小正方形，折成一个无盖的长方体,使它的 底面积为800 cm2. 求截去正方形的边长. 800cm2 x x 解:设截取正方形的边长为 x m. 根据题意,得 (60 - 2x)(40 - 2x) = 800. 整理，得 x2 - 50x + 400 = 0. 解方程,得 x1=10 , x2= 40 (不合题意,舍去). 答:截去正方形的边长为10 cm. (60 - 2x) (40-2x) 例3 1.如图，在矩形ABCD中，AB=6 cm, BC=12 cm，点P从点A开始 沿AB边向点B以1 cm/s的速度移动，点Q从点B开始沿BC向点C 以2 cm/s的速度移动，如果P、Q分别从A、B同时出发，那么几 秒后五边形APQCD的面积为64 cm2？ A B CD Q P分析：求五边形APQCD的面积为64 cm2 时的时间可以 转换为求△PQB面积为（6×12 - 64）cm2的问题. 解:设所需时间为 t s. 根据题意,得 2t (6 - t) ÷2 = 6×12 - 64. 整理，得 t2 - 6t + 8 = 0. 解方程,得 t1 = 2 , t2 = 4 . 故在第2秒和第4秒是五边形面积是 64 cm2 . (6 - t) 2t 2.有这样一道阿拉伯古算题:有两笔钱,一多一少,其和等于20,积 等96,多的一笔被许诺赏给赛义德,那么赛义德得到多少钱? 解: 设赛义德得到钱数为 x . 根据题意,得 x (20 - x) = 96. 整理，得 x 2 - 20x + 96 = 0. 解方程，得 x1 = 12 ， x2 = 8 (不符合题意，舍去). 答：赛义德得到钱数为 12. 3.如图,在Rt△ABC中,∠C=90°,点P、Q同时由A、B两点出发,分 别沿AC、BC方向向点C匀速移动（到点C为止）,它们的速度都 是1 m/s.几秒后△PCQ的面积是Rt△ABC面积的一半? A B C P Q 8m 6m 解：设x秒后，△ PCQ的面积是Rt △ABC面积的一半. 根据题意，得 整理，得 x2 - 14x + 24 = 0. 解方程，得 x1 = 2 , x2 = 12 (不符题意，舍去). 答：2秒后，△ PCQ的面积是Rt △ABC面积 的一半. .))(( 68 2 1 2 168 2 1  xx 利用一元二次方程 解决行程问题 列方程步骤： 应用类型 几何问题 行程问题 面积问题 动点问题 审 设 列 解 检 答