八年级数学上册第2章三角形2-5全等三角形第6课时全等三角形的性质和判定的应用课件 湘教版

八年级数学上册第2章三角形2-5全等三角形第6课时全等三角形的性质和判定的应用课件 湘教版

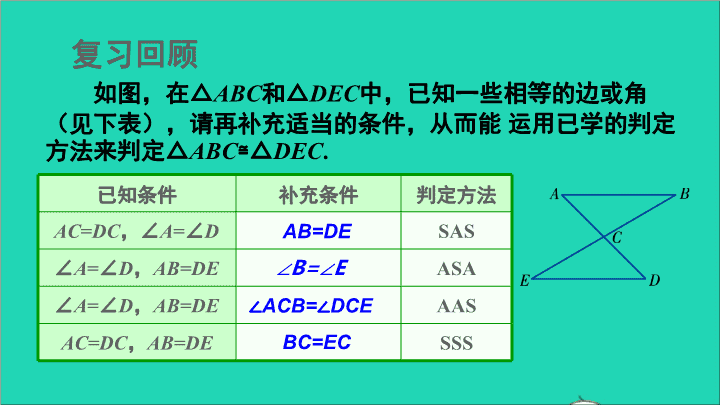
第6课时 全等三角形的性质和判定的应用 2 复习回顾 如图，在△ABC和△DEC中，已知一些相等的边或角 （见下表），请再补充适当的条件，从而能 运用已学的判 定方法来判定△ABC≌ △DEC. 已知条件 补充条件 判定方法 AC=DC，∠A=∠D SAS ∠A=∠D，AB=DE ASA ∠A=∠D，AB=DE AAS AC=DC，AB=DE SSS AB=DE ∠B=∠E ∠ACB=∠DCE BC=EC 推进新课 议一议 根据下列条件，分别画△ABC和△A′B′C′. (1) AB=A′B′=3cm，AC=A′C′=2.5cm，∠B=∠B′=45°； 满足上述条件画出的△ABC和△A′B′C′一定全等吗？ 45°B A 3cm C 2.5cm B′ 45° A′ 3cm C′ 2.5cm 由此你能得出 什么结论？ 结论 两边分别相等且其中一组等边的对角相 等的两个三角形不一定全等. 45°B A 3cm C 2.5cm B′ 45° A′ 3cm C′ 2.5cm 根据下列条件，分别画△ABC和△A′B′C′. (2) ∠A=∠A′=80°，∠B=∠B′=30°，∠C=∠C′=70°. 满足上述条件画出的△ABC和△A′B′C′一定全等吗？ 议一议 30° 80° 70° B A C 30° 80° 70° B′ A′ C′ 由此你能得出什么结论？ 结论 30° 80° 70° B A C 30° 80° 70° B′ A′ C′ 三角分别相等的两个三角形不一定全等. 已知：如图2-55，AC与BD相交于点O，且AB=DC， AC=DB. 求证：∠A=∠D. 例9 证明 连接 BC. 在△ABC和△DCB中， AB = DC， BC = CB（公共边）， AC = DB， ∴ △ABC≌ △DCB （SSS）.∴ ∠A=∠D. 某地在山区修建高速公路时需挖通一条隧道.为估测 这条隧道的长度（如图2-56），需测出这座山A，B间的距 离，结合所学知识，你能给出什么好方法吗？ 例10 图2-56 解：选择某一合适的地点O，使得从O点能测出AO与BO的 长度.连接AO并延长至A′，使OA′=OA；连接BO并延长至 B′，使OB′=OB，连接A′B′，这样就构造出两个三角形. O A′B′ 在△AOB和△A′OB′中， OA = OA′， ∠AOB = ∠A′OB′， OB = OB′， ∴ △AOB≌ △A′OB′（SAS）. ∴ AB=A′B′. 因此只要测出A′B′的长度就能得到这座山A，B间的距离. 图2-56 你还能想出其它方 案，来测出A，B 两处的距离吗？ 练习 已知：如图，AB =AD，BC=DC. 求证：∠B =∠D. 证明 如图，连接AC. 在△ABC和△ADC中， AB=AD， AC=AC（公共边）， BC=DC， 巩固练习 1.如图，已知∠1=∠2，添加一个条件，使得△ABC≌ △ADC， 下列条件添加错误的是（ ） A. ∠B=∠D B. BC=DC C. AB=AD D. ∠3=∠4 B 2.如图，D是AB延长线上一点，DF交AC于点E，AE=CE， FC∥AB，若AB=3，CF=5，则BD的长是（ ） A. 0.5 B. 1 C. 1.5 D. 2 D 3.我国的纸伞工艺十分巧妙.如图，由于在设计时，伞骨上AE ＝AF，支撑杆DE＝DF，所以无论伞张开还是收拢，伞柄AP 始终平分同一平面内两条伞骨所成的角∠BAC，从而保证伞圈 D能沿着伞柄滑动.为了证明这个结论，我们的依据是（ ） A. SSS B. SAS C. AAS D. ASA A 4.如图，王强同学用10块高度都是2cm 的相同长方体小木块，垒了两堵与地面 垂直的木墙，木墙之间刚好可以放进一 个等腰直角三角尺A B C ( A C = B C， ∠ACB=90°)，点C在DE上，点A和点 B分别与木墙的顶端重合，则两堵木墙 之间的距离为__________cm.20 5.如图，AB=CD，AD=BC，DE=BF. 求证：BE=DF. 证明 如图，连接DB. 在△ABD和△CDB中， AB=CD， BD=DB， AD=CB， 5.如图，AB=CD，AD=BC，DE=BF. 求证：BE=DF. 在△EAB和△FCD中， AB=CD， AE=CF， ∠A=∠C， 课后小结 通过本节课的学习，你有什么收获？