- 2021-05-28 发布 |
- 37.5 KB |
- 29页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中物理人教版必修2课件第6章 1行星的运动
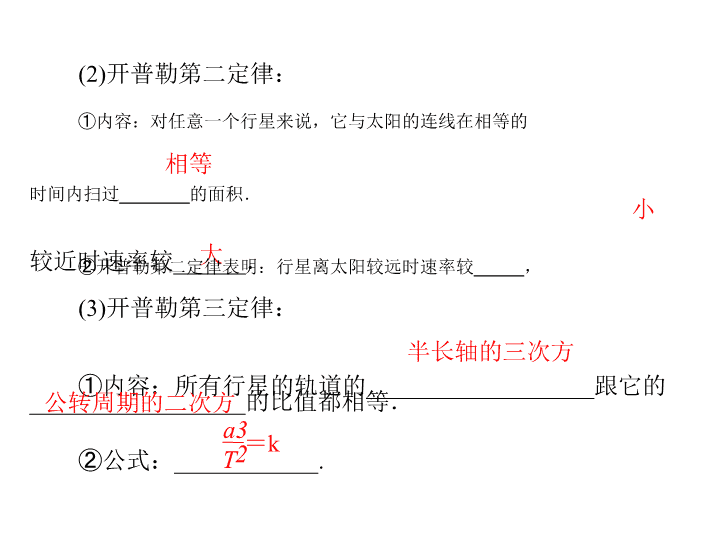
第六章 万有引力与航天 1.行星的运动 1.________认为地球是宇宙的中心,是静止不动的,太阳、 月亮以及其他行星都绕地球运动;________认为太阳是静止不动的,地球和其他行星都绕太阳运动. 地心说 日心说 2.开普勒行星运动定律: 椭圆 焦点 (1) 开普勒第一定律:所有行星绕太阳运动的轨道都是 ______,太阳处在椭圆的一个______上. (2)开普勒第二定律: 相等 小 大 ①内容:对任意一个行星来说,它与太阳的连线在相等的 时间内扫过_______的面积. ②开普勒第二定律表明:行星离太阳较远时速率较_____,较近时速率较______. 半长轴的三次方 (3)开普勒第三定律: ①内容:所有行星的轨道的___________________跟它的 __________________的比值都相等.公转周期的二次方 ②公式:____________.T a3 2=k 3.行星运动的近似处理: 实际上行星的轨道与圆十分接近,可以按圆轨道处理,这样就可以说: 圆心 角速度(或线速度) 匀速圆周 (1)行星绕太阳运动的轨道接近圆,太阳处在_______上. (2)对某一行星来说,它绕太阳做圆周运动的______________ 不变,即行星做____________运动. (3) 所有行星轨道半径的____________ 跟它的公转周期的 __________的比值都相等. 三次方 二次方 4.下列对天体运动规律的认识,其中错误的是( ) A.恒星的相互位置几乎都是固定的,因此恒星是静止的 B.月球绕地球运动,遵循类似于开普勒行星运动定律的规律 A C.地球绕太阳运动的轨道是椭圆,但较接近圆 D.木星与太阳的连线,在相等的时间内扫过的面积相等 知识点1 开普勒第一定律 日心说是真理吗?日心说的提出,是科学与神权的一次 “激烈碰撞”,经过哥白尼、布鲁诺、第谷、开普勒、伽利略 等一大批科学家的不懈努力,最终,科学战胜了神权.如今我 们学习地心说与日心说时,往往会一味地认为托勒密的地心说 是错误的,哥白尼的日心说才是正确的,真的是这样吗? 讨论: (1)随着科学的发展,人类最终认识到地心说和日心说相 比,________更先进.日心说 (2)现在看来,日心说也有其错误之处,其一是将天体的运 动看成是____________运动;其二是把________看成是宇宙的中心. 匀速圆周 太阳 1.内容: 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个 焦点上. 2.理解: 图 6-1-1 所示的是行星绕太阳运动的椭圆轨道,OA 和 OB 是椭圆轨道的半长轴,若太阳位于椭圆轨道的焦点 F1 上,则点 A 称为近日点,点 B 称为远日点. 图 6-1-1 【例 1】关于开普勒第一定律,下列说法不正确的是( ) A.它的发现是建立在天文学家第谷的观测数据之上的 B.该定律中的“所有行星”是指除太阳外太阳系的所有 天体 C.开普勒假设天体不是做匀速圆周运动是发现该定律的 原因之一 D.开普勒执着于计算和观测数据之间的差别是发现该定 律的原因之一 解析:开普勒第一定律中的“所有行星”并不包括太阳系 中行星的卫星,例如月球. 答案:B 【触类旁通】 1.下列不属于开普勒第一定律所具有的意义的是( ) A.说明天体并不是完美地按照圆周轨道来运动的 B.反映了各行星的椭圆轨道的一个焦点都在同一位置上 C.证明了太阳是静止的,静止在椭圆轨道的焦点上D.为日心说提供了有力的证据 C 解析:开普勒第一定律指出太阳处在行星运动椭圆轨道的 一个焦点上,是以太阳为参考系来描述行星运动的,并不是说 太阳静止. 知识点2 开普勒第二定律 经过数十亿年的演化,地球上现存的有记载的生物中,植物 大约有 50 多万种,动物大约有150 多万种,而尚未被发现的现存 生物的种数可能是这总数的 3 倍之多,但现存生物的种数却还不 及地球上曾存在的生物种数的五十分之一. 地球上孕育出如此之多的形形色色的生物,可谓和季节变化 不无关系,然而季节变化正是由于地球公转使地表受太阳光照产 生周期性差异而引起的.当地球位于远日点时,北半球处于夏季, 南半球处于冬季;当地球位于近日点时,北半球处于冬季,南半 球处于夏季. 讨论: (1)季节变化是有周期性的,四季出现一次交替就是地球绕 太阳公转了________.一周 远 近 慢 快 (2)联系季节特点可知,夏至日时地球在________ 日点附 近,冬至日时地球在________日点附近. (3)北半球处于夏季时,地球的公转速度较________;北半 球处于冬季时,地球的公转速度较________. 1.内容: 对任意一个行星来说,它与太阳的连线在相等的时间内扫 过相等的面积.(如图 6-1-2 所示,阴影部分表示行星在相等 时间内扫过的面积.) 2.理解: 由于行星的轨道不是圆,因此行星与太阳的距离在不断地 变化.这个定律告诉我们,当行星离太阳较近时,运行的速度 比较快,而离太阳较远时,运行的速度比较慢. 图 6-1-2 【例 2】我国发射的第一颗人造卫星,其近地点高度 h1= 439 km,远地点高度 h2=2 384 km,求在近地点与远地点上,卫 星运动的速率之比 v1∶ v2.(已知 R地=6 400 km,用 h1、h2、R地表 示,不要求数值计算) 【触类旁通】 2.某行星沿椭圆轨道运行,远日点离太阳的距离为 a,近 日点离太阳的距离为 b,过远日点时行星的速率为 va,则过近日点时的速率 vb 为( )C 解析:由开普勒第二定律可知,行星与太阳的连线在相等 的时间内扫过的面积相等,取Δt 足够短,所扫过的面积近似看 知识点3 开普勒第三定律 2012 年6 月,各大洲相继出现了本世纪第二次金星凌日的 天文奇观,而下一次出现将要等到2117 年.早在1639 年12 月, 英国天文学家耶利米霍罗克斯首次记录到这一天文现象,该现 象为太阳、金星与地球排成一条直线,在地球上我们会观察到 金星如同一个小黑点在炙热的太阳盘面上慢慢移动. 日地距离的测定被誉为“最崇高的天文问题”,1716 年英 国著名天文学家哈雷提出了一种利用观测金星凌日来计算日地 距离的方法:先根据不同地点观测到的金星凌日出现的视差计 算出地球与金星的距离,再结合开普勒第三定律计算出日地距 离.由此算出的结果与现代天文学得出的数据非常接近,十八 和十九世纪的天文学家正是通过这种方法算出日地距离的,该 方法称为时间计量法. 讨论: (1)开普勒第三定律的表达式为________,其中 k 值对于金 星和地球来说是______的,它是只和_____________有关的常量. (2)已知金星和地球的公转周期分别为 T1 和 T2,金星凌日时 得到的金星与地球的距离为 r,试简要分析如何利用时间计量法 测算日地距离 R. 2=k a3 T 相同 太阳(中心天体) 将观测数据代入上式并解方程,即可求得日地距离 R. 提示:由于金星凌日时,太阳、金星与地球在同一直线上, 故此时金星到太阳的距离为 R-r . 1.内容: 所有行星的轨道的半长轴的三次方跟它的公转周期的二次 方的比值都相等. 2.表达式: 若用 a 代表椭圆轨道的半长轴的长度(如图 6-1-3 所示), a3 T2 图 6-1-3 T 代表公转周期的大小,则开普勒第三定律的表达式为—=k 3.理解: (1)开普勒第三定律揭示了轨道和周期之间的关系,椭圆轨 道半长轴越长的行星,其公转周期越大;反之,半长轴越短, 公转周期越小.(2)k 值是一个由被环绕的中心天体本身决定的常量,也就 是说,在中心天体不同的系统里 k 值是不同的,在中心天体相 同的系统里 k 值是相同的. 【例3】哈雷彗星的环绕周期是 76 年,离太阳最近的距离 是 8.9×1010 m,离太阳最远的距离尚未得知.试根据开普勒定 律估算这个最远距离是多少?(k=3.354×1018 m3/s2) 行星 金星 地球 火星 木星 公转周期/年 0.615 1.0 1.88 11.86 【例 4】太阳系八大行星的公转轨道可近似看做圆轨道. 地球与太阳之间的平均距离约为 1.5 亿千米,结合下表可知,火星与太阳之间的平均距离约为( A.1.2 亿千米 ) B.2.3 亿千米 C.4.6 亿千米 D.6.9 亿千米 答案:B 【触类旁通】 3.哈雷彗星最近出现的时间是 1986 年,天文学家哈雷曾 预言,这颗彗星将每隔一定的时间就会出现.请预测其下一次 飞临地球是哪一年?提供以下数据供参考:(1)地球的公转轨道接近圆,哈雷彗星的运动轨迹是一个椭 圆; (2)哈雷彗星轨道的半长轴 a′约等于地球轨道半长轴 a 的 18 倍. 解:设哈雷彗星绕太阳运动的周期为 T′,地球的公转周 期为 T,根据开普勒第三定律有 则哈雷彗星下次临近地球的时间是 1986 年+76 年=2062 年. 4.地球到太阳的距离为水星到太阳距离的 2.6 倍,那么地 球和水星绕太阳运动的速度之比是多少?(设地球和水星绕太 阳运动的轨道为圆) 开普勒行星运动定律的应用 1.开普勒行星运动定律不仅适用于太阳和太阳系行星之间 的关系,还适用于宇宙其他恒星和行星与行星和卫星,即一切 被环绕的中心天体和环绕天体之间的关系,例如月球绕地球运 动、人造卫星绕火星运动等. 2.在实际计算中,为了简化问题,有时能够将一些椭圆轨 道近似看做圆轨道来处理,这样,对应开普勒行星运动定律, 有以下结论: (3)在表达式 =k中,k值仍然只与中心天体有关,但a变 为行星运行圆轨道的半径r,即 =k. (1)行星绕行的圆轨道只是椭圆轨道的一种特殊情况,太阳 处在圆心上. (2)当行星做匀速圆周运动时,角速度和线速度大小不变, 因此与太阳的连线在相等的时间内扫过的面积必然相等.a3 T2 r3 T2查看更多