- 2021-05-28 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第27讲 表面积与体积(一)
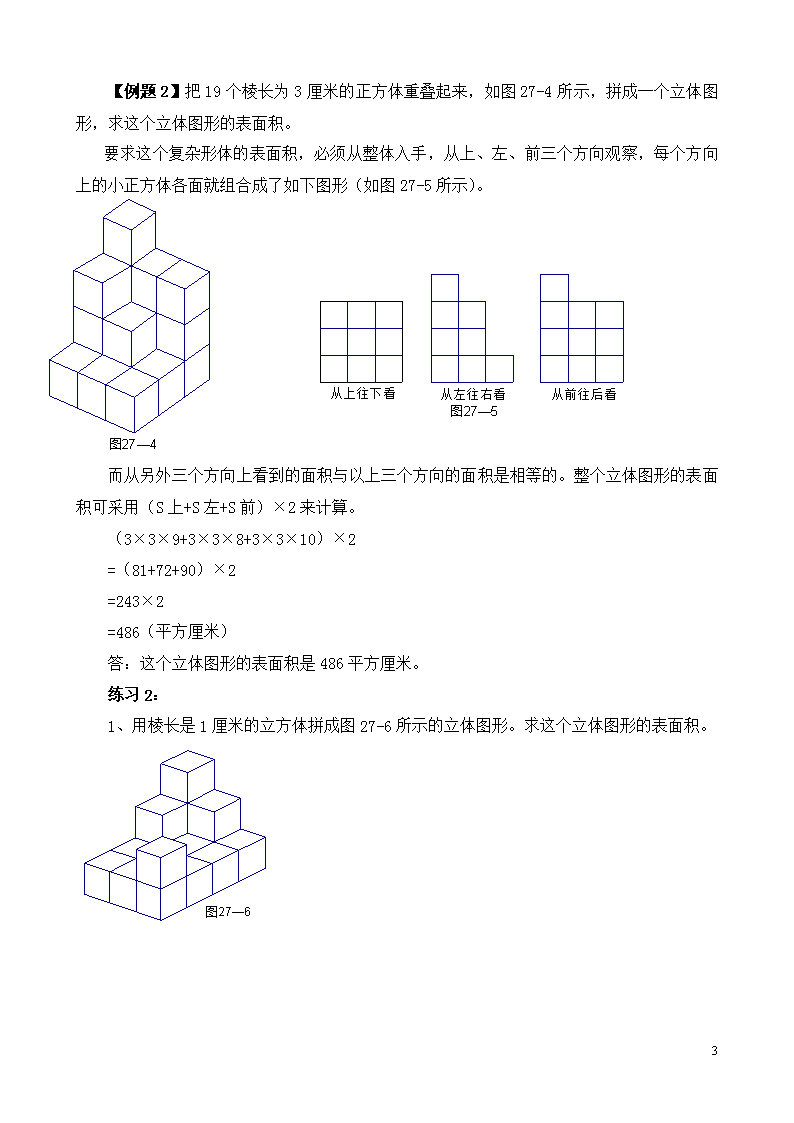
第27讲 表面积与体积(一) 一、知识要点 小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。从平面图形到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力。因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数、形”结合的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算。 在解答立体图形的表面积问题时,要注意以下几点: (1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点。 (2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍。反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍。 (3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来。若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。 二、精讲精练 【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少? 这是一道开放题,方法有多种: ①按图27-1所示,沿着一条棱挖,剩下部分的表面积为592平方厘米。 ②按图27-2所示,在某个面挖,剩下部分的表面积为632平方厘米。 7 ③按图27-3所示,挖通某两个对面,剩下部分的表面积为672平方厘米。 练习1: 1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体,剩下部分的表面积是多少? 2、把一个长为12分米,宽为6分米,高为9分米的长方体木块锯成两个想同的小厂房体木块,这两个小长方体的表面积之和,比原来长方体的表面积增加了多少平方分米? 3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面积会发生怎样的变化? 7 【例题2】把19个棱长为3厘米的正方体重叠起来,如图27-4所示,拼成一个立体图形,求这个立体图形的表面积。 要求这个复杂形体的表面积,必须从整体入手,从上、左、前三个方向观察,每个方向上的小正方体各面就组合成了如下图形(如图27-5所示)。 而从另外三个方向上看到的面积与以上三个方向的面积是相等的。整个立体图形的表面积可采用(S上+S左+S前)×2来计算。 (3×3×9+3×3×8+3×3×10)×2 =(81+72+90)×2 =243×2 =486(平方厘米) 答:这个立体图形的表面积是486平方厘米。 练习2: 1、用棱长是1厘米的立方体拼成图27-6所示的立体图形。求这个立体图形的表面积。 7 2、一堆积木(如图27-7所示),是由16块棱长是2厘米的小正方体堆成的。它们的表面积是多少平方厘米? 图27-7 3、一个正方体的表面积是384平方厘米,把这个正方体平均分割成64个相等的小正方体。每个小正方体的表面积是多少平方厘米? 【例题3】把两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,这个大长方体的表面积最少是多少平方厘米? 把两个相同的大长方体拼成一个大厂房体,需要把两个相同面拼合,所得大厂房体的表面积就减少了两个拼合面的面积。要使大长方体的表面积最小,就必须使两个拼合面的面积最大,即减少两个9×7的面。 (9×9+9×4+7×4)×2×2—9×7×2 =(63+36+28)×4—126 =508—126 =382(平方厘米) 答:这个大厂房体的表面积最少是382平方厘米。 练习3: 1、把底面积为20平方厘米的两个相等的正方体拼成一个长方体,长方体的表面积是多少? 7 2、将一个表面积为30平方厘米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体。求大长方体的表面积是多少。 3、用6块(如图27-8所示)长方体木块拼成一个大长方体,有许多种做法,其中表面积最小的是多少平方厘米? 图27-8 【例题4】一个长方体,如果长增加2厘米,则体积增加40立方厘米;如果宽增加3厘米,则体积增加90立方厘米;如果高增加4厘米,则体积增加96立方里,求原长方体的表面积。 我们知道:体积=长×宽×高;由长增加2厘米,体积增加40立方厘米,可知宽×高=40÷2=20(平方厘米);由宽增加3厘米,体积增加90立方厘米,可知长×高=90÷3=30(平方厘米);由高增加4厘米,体积增加96立方厘米,可知长×宽=96÷4=24(平方厘米)。而长方体的表面积=(长×宽+长×高+宽×高)×2=(20+30+24)×2=148(平方厘米)。即 40÷2=20(平方厘米) 90÷3=30(平方厘米) 96÷4=24(平方厘米) (30+20+24)×2 =74×2 =148(平方厘米) 答:原长方体的表面积是148平方厘米。 7 练习4: 1、一个长方体,如果长减少2厘米,则体积减少48立方厘米;如果宽增加5厘米,则体积增加65立方厘米;如果高增加4厘米,则体积增加96立方厘米。原来厂房体的表面积是多少平方厘米? 2、一个厂房体木块,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,其表面积减少了120平方厘米。原来厂房体的体积是多少立方厘米? 3、有一个厂房体如下图所示,它的正面和上面的面积之和是209。如果它的长、宽、高都是质数,这个长方体的体积是多少? 图27-9 【例题5】如图27-10所示,将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体。求这个物体的表面积。 如果分别求出三个圆柱的表面积,再减去重叠部分的面积,这样计算比较麻烦。实际上三个向上的面的面积和恰好是大圆柱的一个底面积。这样,这个物体的表面积就等于一个大圆柱的表面积加上中、小圆柱的侧面积。 3.14×1.5×1.5×2+2×3.14×1.5×1+2×3.14×1×1+2×3.14×0.5×1 =3.14×(4.5+3+2+1) =3.14×10.5 =32.97(平方米) 答:这个物体的表面积是32.97平方米。 7 练习5: 1、一个棱长为40厘米的正方体零件(如图27-11所示)的上、下两个面上,各有一个直径为4厘米的圆孔,孔深为10厘米。求这个零件的表面积。 2、用铁皮做一个如图27-12所示的工件(单位:厘米),需用铁皮多少平方厘米? 3、如图27-13所示,在一个立方体的两对侧面的中心各打通一个长方体的洞,在上、下侧面的中心打通一个圆柱形的洞。已知立方体棱长为10厘米,侧面上的洞口是边长为4厘米的正方形,上、下侧面的洞口是直径为4厘米的圆,求该立方体的表面积和体积(π取3.14)。 7 7查看更多