- 2021-05-28 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市崇明区2021届高三数学上学期一模试题(Word版附答案)
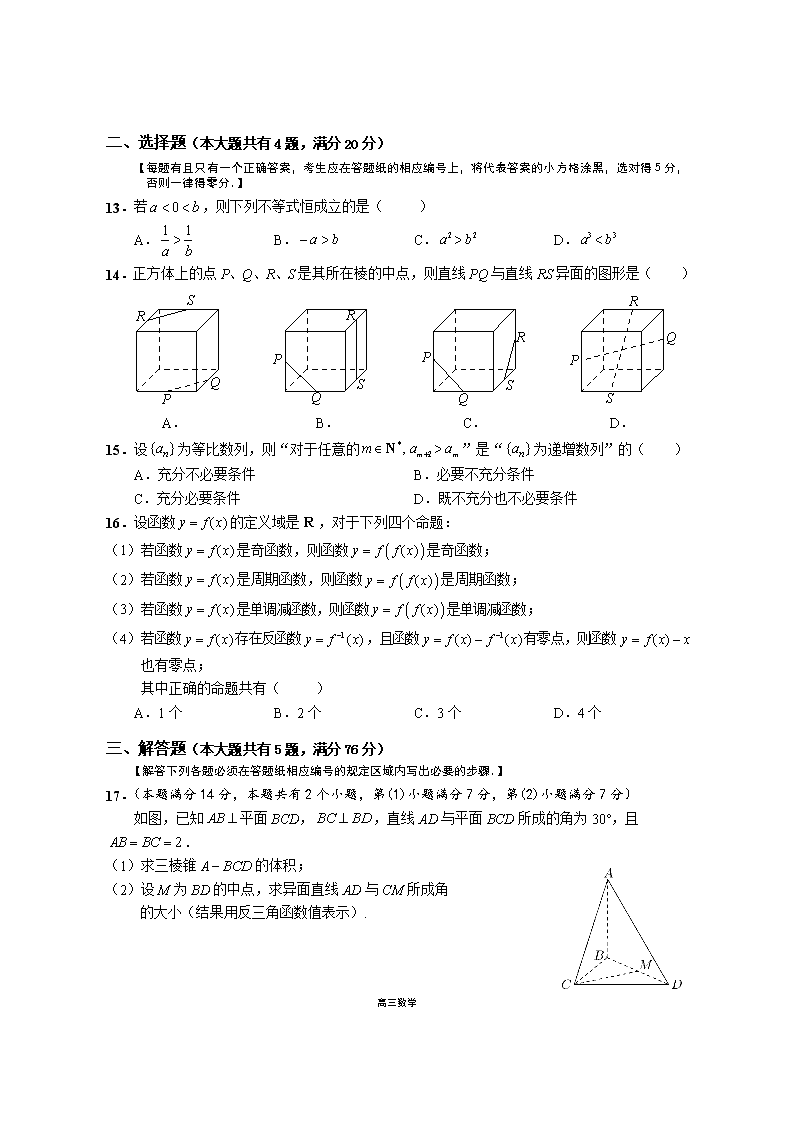
高三数学 崇明区 2021 届第一次高考模拟考试试卷 数 学 考生注意: 1. 本试卷共 4 页,21 道试题,满分 150 分,考试时间 120 分钟. 2. 本试卷分设试卷和答题纸.试卷包括试题与答题要求.作答必须涂(选择题)或写(非选择 题)在答题纸上,在试卷上作答一律不得分. 3. 答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息. 一、填空题(本大题共有 12 题,满分 54 分,其中 1~6 题每题 4 分,7~12 题每题 5 分) 【考生应在答题纸相应编号的空格内直接填写结果.】 1.设集合 {1, 2, 3}A ,集合 {3, 4}B ,则 A B . 2.不等式 1 02 x x 的解集是 . 3.已知复数 z 满足 (z 2)i 1 (i 是虚数单位),则 z . 4.设函数 1( ) 1f x x 的反函数为 1( )f x ,则 1(2)f . 5.点 (0,0) 到直线 2x y 的距离是 . 6.计算: 1 2 3lim ( 2)n n n n . 7.若关于 x、y 的方程组 4 6 1 3 2 x y ax y 无解,则实数 a . 8.用数字 0、1、2、3、4、5 组成无重复数字的三位数,其中奇数的个数为 .(结 果用数值表示) 9.若 2 3(2 )na b 的二项展开式中有一项为 4 12ma b ,则 m . 10.设 O 为坐标原点,直线 x a 与双曲线 2 2 2 2: 1 ( 0, 0)x yC a ba b 的两条渐近线分别交 于 ,D E 两点,若 ODE△ 的面积为 1,则双曲线 C 的焦距的最小值为 . 11.已知函数 ( )y f x ,对任意 x R ,都有 ( 2) ( )f x f x k ( k 为常数),且当 [0,2]x 时, 2( ) 1f x x ,则 (2021)f . 12.已知点 D 为圆 2 2: 4O x y 的弦 MN 的中点,点 A 的坐标为 (1, 0) ,且 1AM AN ,则 OA OD uur uuur 的范围是 . 高三数学 二、选择题(本大题共有 4 题,满分 20 分) 【每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得 5 分, 否则一律得零分.】 13.若 0a b ,则下列不等式恒成立的是( ) A. 1 1 a b B. a b C. 2 2a b D. 3 3a b 14.正方体上的点 P、Q、R、S 是其所在棱的中点,则直线 PQ 与直线 RS 异面的图形是( ) A. B. C. D. 15.设{ }na 为等比数列,则“对于任意的 * 2, m mm a a N ”是“{ }na 为递增数列”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 16.设函数 ( )y f x 的定义域是 R ,对于下列四个命题: (1)若函数 ( )y f x 是奇函数,则函数 ( )y f f x 是奇函数; (2)若函数 ( )y f x 是周期函数,则函数 ( )y f f x 是周期函数; (3)若函数 ( )y f x 是单调减函数,则函数 ( )y f f x 是单调减函数; (4)若函数 ( )y f x 存在反函数 1( )y f x ,且函数 1( ) ( )y f x f x 有零点,则函数 ( )y f x x 也有零点; 其中正确的命题共有( ) A.1 个 B.2 个 C.3 个 D.4 个 三、解答题(本大题共有 5 题,满分 76 分) 【解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.】 17.(本题满分 14 分,本题共有 2 个小题,第(1)小题满分 7 分,第(2)小题满分 7 分) 如图,已知 AB 平面 BCD,BC BD ,直线 AD 与平面 BCD 所成的角为 30°,且 2AB BC . (1)求三棱锥 A BCD 的体积; (2)设 M 为 BD 的中点,求异面直线 AD 与 CM 所成角 的大小(结果用反三角函数值表示). 18.(本题满分 14 分,本题共有 2 个小题,第(1)小题满分 6 分,第(2)小题满分 8 分) S R P Q Q P R S Q P S R R P S Q 高三数学 已知函数 21( ) sin2 3cos2f x x x . (1)求函数 ( )y f x 的最小正周期; (2)在 ABC△ 中,角 A,B,C 的对边分别为 a,b,c.若锐角 A 满足 1 3( ) 2f A , 6C , 2c ,求 ABC△ 的面积. 19.(本题满分 14 分,本题共有 2 个小题,第(1)小题满分 6 分,第(2)小题满分 8 分) 研究表明:在一节 40 分钟的网课中,学生的注意力指数 y 与听课时间 x(单位:分钟) 之间的变化曲线如图所示. 当 [0,16]x 时 , 曲 线 是 二 次 函 数 图 像 的 一 部 分 ; 当 [16, 40]x 时 , 曲 线 是 函 数 0.8log ( ) 80y x a 图像的一部分.当学生的注意力指数不高于 68 时,称学生处于“欠佳听课 状态”. (1)求函数 ( )y f x 的解析式; (2)在一节 40 分钟的网课中,学生处于“欠佳听课状态” 的时间有多长?(精确到 1 分钟) y x1216 40 80 84 O ·· · ·· ·· · 高三数学 20.(本题满分 16 分,本题共有 3 个小题,第(1)小题满分 4 分,第(2)小题满分 5 分,第(3)小 题满分 7 分) 已知椭圆 2 2: 14 x y 的左右顶点分别为 A、B,P 为直线 4x 上的动点,直线 PA 与椭圆 的另一交点为 C,直线 PB 与椭圆 的另一交点为 D. (1)若点 C 的坐标为 (0,1) ,求点 P 的坐标; (2)若点 P 的坐标为 (4,1) ,求以 BD 为直径的圆的方程; (3)求证:直线 CD 过定点. 21.(本题满分 18 分,本题共有 3 个小题,第(1)小题满分 4 分,第(2)小题满分 6 分,第(3)小 题满分 8 分) 对于数列{ }na ,若从第二项起的每一项均大于该项之前的所有项的和,则称{ }na 为 P 数列. (1)若数列1, 2, , 8x 是 P 数列,求实数 x 的取值范围; (2)设数列 1 2 3 10, , , ,a a a a 是首项为 1 、公差为 d 的等差数列,若该数列是 P 数列, 求 d 的取值范围; (3)设无穷数列{ }na 是首项为 a、公比为 q 的等比数列,有穷数列{ }nb ,{ }nc 是从{ }na 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别记为 1T , 2T . 求证:当 0a 且 1 2T T 时,数列{ }na 不是 P 数列. 高三数学 崇明区 2021 届第一次高考模拟考试(数学)参考答案及评分标准 一、填空题 1. {3}; 2. ( 2,1) ; 3. 2 i ; 4. 1 2 ; 5. 2 ; 6. 1 2 ; 7. 2 ; 8.48; 9.60; 10. 2 2 ; 11. 2; 12.[-1,2). 二、选择题 13.D; 14.B; 15.C; 16.B 三、解答题 17.解:(1)因为 AB 平面 BCD, 所以 ADB 就是直线 AD 与平面 BCD 所成的角,所以 30ADB ...............3 分 所以 2 3BD , 所以 1 4 33 3A BCD BCDV S AB ...........................7 分 (2)取线段 AB 的中点 N ,联结CN 、 MN ,则 / /MN AD 所以 CMN 就是异面直线 AD 与 CM 所成的角...........................4 分 在 CMN 中, 2MN , 5CN , 7CM 所以 2 2 2 3 7cos 2 14 CM MN CNCMN CM MN ...........................7 分 18.解:(1) 1 3(1 cos2 ) 3( ) sin2 sin(2 )2 2 3 2 xf x x x ...........................4 分 所以函数 ( )y f x 的最小正周期 2 | |T ...........................6 分 (2)由 1 3( ) 2f A ,得: 1sin(2 )=3 2A 因为 (0, )2A ,所以 22 ( , )3 3 3A ,所以 2 =3 6A , 4A ...........................3 分 所以 2 2 2 2 4 2cos 2 4 2 b c a bA bc b ,所以 2 6 2b ...........................6 分 所以 1 sin 3 12ABCS bc A ...........................8 分 19.解:(1)当 [0,16]x 时,设 2( ) ( 12) 84( 0)f x b x b 由 (16) 80f ,得: 2(16 12) 84=80b ,故 1 4b ...........................2 分 当 [16, 40]x 时,由 (16) 80f ,得: 0.8log (16 ) 80 80a ,故 15a .................4 分 高三数学 所以 2 0.8 1 ( 12) 84, [0,16]( ) 4 log ( 15) 80, (16,40] x xf x x x ...........................6 分 (2)当 [0,16]x 时,由 21 ( 12) 84 684 x ,得: [0,4]x ...........................3 分 当 [16, 40]x 时,由 0.8log ( 15) 80 68x ,得: 1215 0.8 29.6x 所以 [30,40]x ...........................3 分 因此,在一节 40 分钟的网课中,学生处于“欠佳听课状态”的时间有 14 分钟..............8 分. 20. 解:(1)由题意, ( 2,0)A ,直线 AP 的方程是: 12 x y ...........................3 分 由 12 4 x y x ,得:点 P 的坐标是(4,3)...........................4 分 (2)由题意, (2,0)B ,直线 PB 的方程是: 2 2 x y ,代入 2 2 14 x y ,得: 2 2 0x x ,解得: 0x ,或 2x ,所以点 D 坐标为(0,-1), 线段 BD中点为 1(1, )2 ,| | 5BD ...........................3 分 所以以 BD 为直径的圆的方程是 2 21 5( 1) ( )2 4x y ...........................5 分 (3)设 0(4, )P y , 1 1( , )C x y , 2 2D( , )x y ,则直线 AP 的方程是: 0 ( 2) 6y x y 代入 2 2 14 x y ,得: 2 2 2 2 0 0 0(9 ) 4 4 36 0y x y x y 所以 2 0 1 2 0 2 18= 9 yx y , 0 1 2 0 6 9 yy y 同理,可得: 2 0 2 2 0 2 2= 1 yx y , 0 2 2 0 2 1 yy y ..........................4 分 所以直线CD 的方程为: 2 2 2 0 0 0 0 0 0 2 2 2 2 2 2 0 0 0 0 0 0 2 6 2 2 2 2 2 18 2( )( ) ( )( )1 9 1 1 9 1 y y y y y yx yy y y y y y 令 0y ,得: 1x 所以直线CD 过定点(1,0)..........................7 分 21.解:(1)由题意,得: 1 2 8 1 2 x x ,所以3 5x ..........................4 分 (2)由题意知,该数列的前 n 项和为 ( 1) 2n n nS n d , 1 1na nd , 高三数学 由数列 1 2 3 10, , , ,a a a a 是 P 数列,可知 2 1 1a S a ,故公差 0d ..........................3 分 2 1 31 1 02 2n n dS a n d n 对满足 1,2,3 ,9n 的任意 n 都成立,则 2 39 9 1 1 02 2 d d ,解得 8 27d , 故 d 的取值范围为 80, 27 ..........................6 分 (3)若 na 是 P 数列,则 1 2a S a aq , 因为 0a ,所以 1q ,又由 1n na S 对一切正整数 n 都成立,可知 1 1 n n qaq a q ,即 12 n q q 对一切正整数 n 都成立, 由 1 0 n q , 1lim 0 n n q ,故 2 0q ,可得 2q ..........................3 分 若 nb 中的每一项都在 nc 中,则由这两数列是不同数列,可知 1 2T T ; 若 nc 中的每一项都在 nb 中,同理可得 1 2T T> ; 若 nb 中至少有一项不在 nc 中且 nc 中至少有一项不在 nb 中, 设 nb , nc 是将 nb , nc 中的公共项去掉之和剩余项依次构成的数列,它们的所有项和 分别为 1T , 2T , 不妨设 nb , nc 中最大的项在 nb 中,设为 )2(ma m , 则 2 1 2 1 1m mT a a a a T ,故 2 1T T ,故总有 1 2T T 与 1 2T T 矛盾,故假设错误, 原命题正确...........................8 分查看更多