- 2021-05-28 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学八年级上册同步练习课件-第13章-13逆命题与逆定理
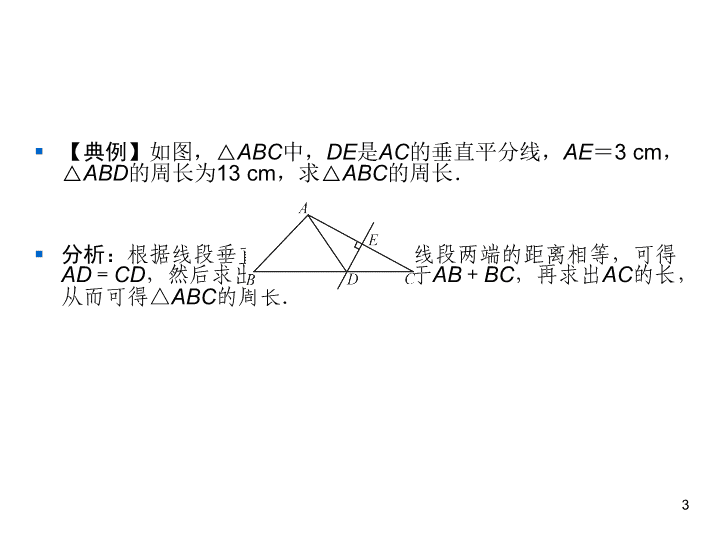
第13章 全等三角形 13.5 逆命题与逆定理 2 线段垂直平分线(第二课时) § 知识点1 线段垂直平分线的性质定理 § 线段垂直平分线上的点到线段两端的距离相 等. § 注意:(1)使用线段垂直平分线的性质时直线 要满足以下两个条件:①经过线段的中点; ②垂直这条线段. § (2)线段的垂直平分线有时也被称为线段的中 垂线. 2 § 【典例】如图,△ABC中,DE是AC的垂直平分线,AE=3 cm, △ABD的周长为13 cm,求△ABC的周长. § 分析:根据线段垂直平分线上的点到线段两端的距离相等,可得 AD=CD,然后求出△ABD的周长等于AB+BC,再求出AC的长, 从而可得△ABC的周长. 3 § 解答:∵DE是AC的垂直平分线,AE=3 cm, § ∴AD=CD,AC=2AE=2×3=6(cm), § ∴△ABD的周长=AB+BD+AD=AB+BD +CD=AB+BC=13 cm, § ∴△ABC的周长=AB+BC+AC=13+6= 19(cm). § 点评:线段垂直平分线的性质是证明线段相 等的重要方法之一,它是由“垂直平分”得 到“线段相等”. 4 § 知识点2 线段垂直平分线的性质定理的逆定 理 § 到线段两端距离相等的点在这条线段的垂直 平分线上. § 拓展:三角形三边的垂直平分线交于一点, 且这点到三角形三个顶点的距离相等. 5 § 1.如图,直线CD是线段AB的垂直平分线, P为直线CD上的一点,已知线段PA=5,则 线段PB的长度为 ( ) § A.6 B.5 § C.4 D.3 6 B § 2.如图所示,CD是AB的垂直平分线,若 AC=1.6 cm,BD=2.3 cm,则四边形ABCD 的周长是 ( ) § A.3.9 cm § B.7.8 cm § C.4 cm § D.4.6 cm 7 B § 3.【2018·湖北黄冈中考】如图,在△ABC中,DE是AC的垂直 平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=25°, 则∠BAD为 ( ) § A.50° B.70° § C.75° D.80° 8 B § 4.如图,DE是边AC的垂直平分线,若BC =15,AD=7,则BD=_____. 9 8 5.【2018·贵州毕节中考】如图,在△ABC中,AC=10,BC=6,AB的垂 直平分线交AB于点D,交AC于点E,则△BCE的周长是______.16 § 6.某公园有海盗船、摩天轮、碰碰车三个娱乐 设施,现要在公园内建一个售票中心,使得三个 娱乐设施所处位置到售票中心的距离相等,请在 图中确定售票中心的位置. 10 解:如图,连结AB、AC.分别作线段AB、AC的垂直平分线,两垂直平分线 相交于点P,则点P即为售票中心的位置. § 7.如图,AB=AC,AB的垂直 平分线DE交BC的延长线于点E, 交AC于点F,∠A=50°,AB +BC=6.求: § (1)△BCF的周长; § (2)∠E的度数. 11 解:(1)∵DE是AB的垂直平分线,∴AF=BF,∴△BCF的周长为CF+BF+ BC=CF+AF+BC=AC+BC=AB+BC=6. (2)∵AB=AC,∠A=50°,∴∠ABC=∠ACB=65°.∵DE垂直平分AB, ∴∠EDB=90°,∴∠E=∠EDB-∠DBE=90°-65°=25°. § 8.如图,点D是线段AB、AC的中垂线的交 点,且∠A=130°,连结BD、CD,则 ∠BDC的度数为 ( ) § A.90° § B.100° § C.120° § D.130° 12 B § 9.如图,在△ABC中,AB、AC的垂直平分 线l1、l2相交于点O,若∠BAC等于82°,则 ∠OBC等于 ( ) § A.8° B.9° § C.10° D.11° 13 A § 10.在等腰△ABC中,AB=AC,AB的垂直 平分线DE与AC所在的直线相交所成的锐角 是40°,则∠ABC= ( ) § A.40°或60° B.65° § C.25°或65° D.35°或125° § 11.【2018·四川南充中考】如图,在 △ABC中,AF平分∠BAC,AC的垂直平分 线DE交BC于点E,∠B=70°,∠FAE= 19°,则∠C=________. 14 C 24° § 12.如图,在△ABC中,∠C=90°,DE是 AB的垂直平分线,连结AD,若BD=3CD, 则S△AED∶ S△ABC=________. 15 3∶ 8 § 13.在△ABC中,AB边的垂直平分线l1交BC 于点D,AC边的垂直平分线l2交BC于点E,l1 与l2相交于点O,△ADE的周长为6 cm. § (1)求BC的长; § (2)分别连结OA、OB、OC,若△OBC的周 长为16 cm,求OA的长. 16 § 解:(1)如图,∵l1、l2分别是线段AB、AC的 垂直平分线,∴AD=BD,AE=CE,∴AD +DE+AE=BD+DE+CE=BC.∵△ADE 的周长为6 cm,即AD+DE+AE=6 cm, ∴BC=6 cm. (2)连结OA、OB、OC.∵AB 边的垂直平分线l1交BC于点D,AC边的垂直 平分线l2交BC于点E,∴OA=OC= OB.∵△OBC的周长为16 cm,即OC+OB+ BC=16 cm,∴OC+OB=16-6=10(cm), ∴OB=OC=5 cm,∴OA=5 cm. 17 § 14.如图,在△ABC中,AB= AC,AB的垂直平分线交AB于 点N,交BC的延长线于点M. § (1)若∠A=40°,求∠NMB的 度数; § (2)如果将(1)中∠A的度数改为 70°,其余条件不变,再求 ∠NMB的度数; 18 (3)你发现有什么样的规律?试证明这个规律; (4)若将(1)中的∠A改为钝角,(3)中的规律是否仍然成立? 19查看更多