八年级上数学课件- 13-3-2 等边三角形 课件（共21张PPT）_人教新课标

八年级上数学课件- 13-3-2 等边三角形 课件（共21张PPT）_人教新课标

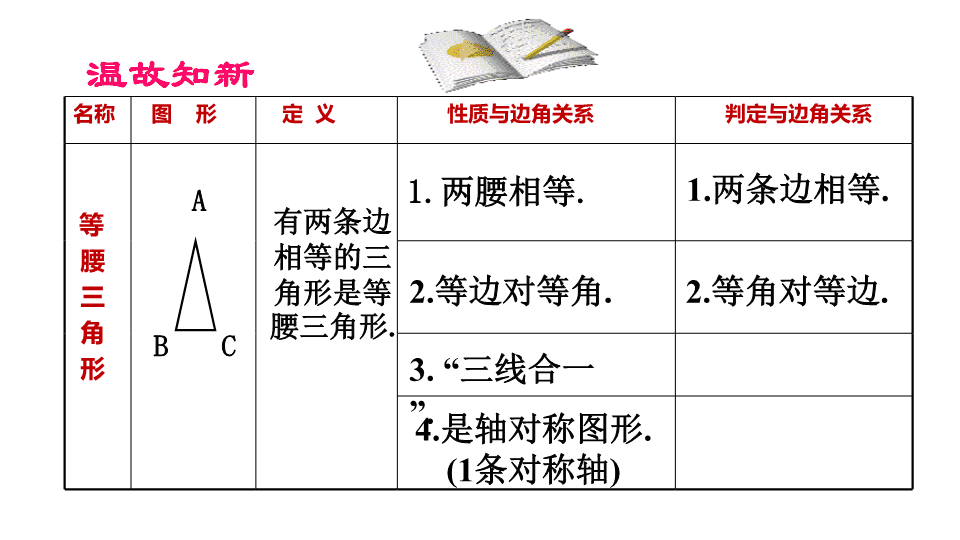
八年级上册数学 第十三章 轴对称 13.3.2 等边三角形 名称 图 形 定 义 性质与边角关系 判定与边角关系 等 腰 三 角 形 A B C 有两条 边相等 的三角 形是等 腰三角 形. 2.等边对等角. 3. “三线合一”. 4.是轴对称图形. (1条对称轴) 2.等角对等边. 1.两条边相等.1.两腰相等. 温故知新 等边三角形定义：三条边都相等的三角形叫做等边 三角形. 我们前面学习三角形分类时，学过一种特殊的等腰三角形 是什么三角形？ 1.把等腰三角形的性质用于等边三角形，能得到什么 结论？ 1.等边三角形的内角都相等吗?为什么? 等边三角形性质探索: A B C 已知：AB=AC=BC 求证：∠A= ∠ B=∠C= 60°. A B C 等边三角形性质探索: A B C 等边三角形性质探索: 名 称 图 形 性质与边角关系 等 边 三 角 形 A B C 2.三个角都相等，且都为60°. 3.“三线合一”. 1.三条边都相等. 4.是轴对称图形，有三条对称轴. 思考题 ？ 2.一个三角形满足什么条件 就是等边三角形? 已知：如图，⊿ABC中， ∠ A=∠B=∠C. 求证：AB=AC=BC. A B C 证明：在⊿ABC中， ∵ ∠ A=∠B（已知）, ∴BC=CA（等角对等边）. 同理 CA=AB. ∴BC=CA=AB. ⒈ 三个角都相等的三角形是等边三角形吗？ 等边三角形判定探索: 问题：如果一个等腰三角形中有一个角是60°， 那么这个三角形是什么三角形？ 分类讨论： 等边三角形判定探索: 有一个内角是60 °的等腰三角形是什么三角形？ 假若AB=AC，则∠ B= ∠ C. 1.当顶角∠A=60 °时,∠ B= ∠ C= 60 °. ∴ ∠A= ∠ B= ∠ C=60 °. ∴ △ABC是等边三角形. 2.当底角∠ B= 60时,∠ C=60 °, ∠A=180 -(60 °+60 °)=60. ° ∴ ∠A= ∠ B= ∠ C=60 °. ∴ △ABC是等边三角形. A B C 等边三角形判定探索: 等边三角形判定方法： 有一个角是60 °的等腰 三角形是等边三角形. 名 称 图 形 判定与边角关系 等 边 三 角 形 A B C 例4，课本(P80),如图：△ABC是等边三角形，DE//BC,分别 交AB，AC于点D，E点. 求证：△ADE是等边三角形. A D E B C 证明： ∵△ABC是等边三角形, ∵DE∥BC, 想一想，本题还有 其他证法吗？ D 60 ° 60 ° 60 ° 60 ° 60 ° C A B E 在等边三角形ABC中，若 DE // BC，分别交AB， AC于点D，E点. 则△ADE是什么 三角形？ △ADE是等边三角 形. A D E B C 延伸：（小组合作探究）已知: △ABC是等边三角形 （1）如中图：当DE // BC时，若点D、E分别在AB、AC的延长线上，结论依然成立吗？ （2）如右图：当DE // BC时，若点D、E分别在AB、AC的反向延长线上，结论依然成立吗？ 例4，课本(P80),如左图：△ABC是等边三角形，DE//BC,分别交AB，AC于点D，E点. 求证：△ADE是等边三角形. D E B C A A B C D E 1.已知△ABC中，∠A=∠B=60°，AB=3cm, 则 △ABC的周长_______. 2. △ABC是等腰三角形，周长为15cm且∠A=60°，则BC=_______. 9cm 5cm 3.如图，等边三角形ABC中，AD是BC上的高，BDE=∠CDF=60°, 图中有哪些与BD相等的线段？ A B E D F C CD,CF,BE,DE,FD,AF,AE （P93) 如图，D、E、F分别是 等边三角形ABC三边上三点，且 AD=BE=CF. 试问：△DEF是什么三角形？ B E A C D F 等腰三角形 等边三角形 性质 1. 两腰相等 2. 等边对等角 3. “三线合一” （底边上的中线、高线、 顶角的角平分 线） 4.是轴对称图形(1条对称轴) 1. 三条边相等 2. 三个角相等（都为600 ） 3. “三线合一” （每条边上的中线、高线、对角的角平 分线） 4.是轴对称图形(3条对称轴) 判定 1、定义（两条边相等） 2、等角对等边 1、定义（三条边相等） 2、三个角相等 3、有一个角是600 的等腰三角形 比一比 等边三角形是一种特殊的等腰三角形，你能述说等边三角形与 等腰三角形在定义，性质和判定的异同吗? (1)习题13.3(P83) 基础题: 12题 提高题: 14题 (2)本课练习册习题 课后作业 不经历风雨，怎能见彩虹！ 没有人能随随便便成功！ 再见！