- 2021-05-28 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学九年级上册同步课件-1第一章-1菱形的性质与判定
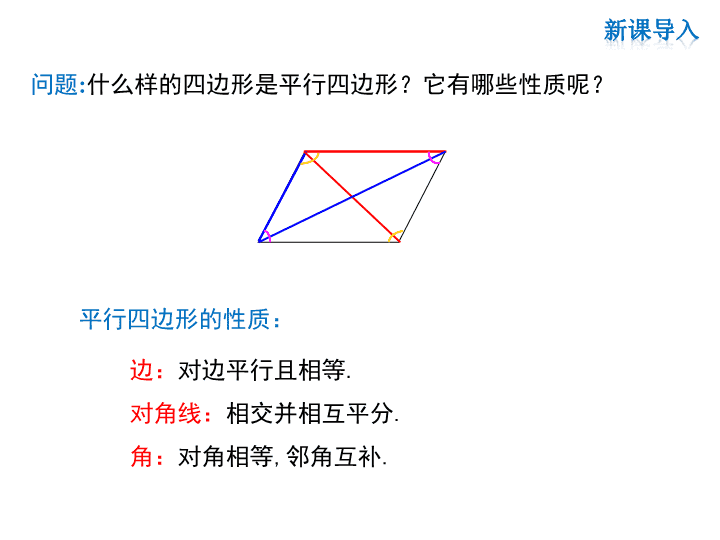
第一章 特殊平行四边形 1.1 菱形的性质与判定 第1课时 菱形的性质 1.了解菱形的概念及其与平行四边形的关系; 2.探索并证明菱形的性质定理.(重点) 3.应用菱形的性质定理解决相关问题.(难点) 学习目标 问题:什么样的四边形是平行四边形?它有哪些性质呢? 平行四边形的性质: 边:对边平行且相等. 对角线:相交并相互平分. 角:对角相等,邻角互补. 活动: 观察下列图片, 找出你所熟悉的图形. 问题1: 观察上图中的这些平行四边形,你能发现它们有什么 样的共同特征? 平行四边形 菱形 菱形:有一组邻边相等的平行四边形叫做菱形. 菱形的概念及其与平行四边形的关系1 菱形是特殊的平行四边形,它具有平行四边形的所 有性质,但平行四边形不一定是菱形. 问题2: 菱形与平行四边形有什么关系? 归纳: 平行四边形 菱形 平行四边形 做一做 请同学们用菱形纸片折一折,回答下列问题: (1)菱形是轴对称图形吗?如果是,它有几条对称 轴?对称轴之间有什么位置关系? (2)菱形中有哪些相等的线段? 菱形的性质2 1.菱形是轴对称图形,有两条对称轴(对称轴为直线 AC和直线BD). 2.菱形四条边都相等(AB=BC=CD=AD). 3.菱形的对角线互相垂直(AC⊥BD). A B C O D 发现菱形的性质 已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交 于点O. 求证:(1)AB = BC = CD =AD; (2)AC⊥BD. 证明菱形的性质 证明:(1)∵四边形ABCD是菱形, ∴AB = CD,AD = BC(菱形的对边相等). 又∵AB=AD; ∴AB = BC = CD =AD. A B C O D 求证:菱形的四条边相等,对角线互相垂直. 思考:菱形的一条对角线所分成的两个内角有什么关系? 试证明AC平分∠BAD和∠BCD, BD平分∠ABC和 ∠ADC. (2)∵AB=AD, ∴△ABD是等腰三角形. 又∵四边形ABCD是菱形, ∴OB=OD. 在等腰三角形ABD中, ∵OB=OD, ∴AO⊥BD, 即AC⊥BD. A B C O D 菱形是特殊的平行四边形,它除具有平行四边形的所有性 质外,还有平行四边形所没有的特殊性质. 对称性:是轴对称图形. 边:四条边都相等. 对角线:互相垂直. 角:对角相等,邻角互补. 边:对边平行且相等. 对角线:相交并相互平分. 1.如图,在菱形ABCD中,两条对角线 AC与BD相交于点O,图中的等腰三角 形有______________________________, 直角三角形有_____________________________ ,而且它们 ________(“全等”或“不全等”). 抢答: 2.菱形具有而平行四边形不一定具有的性质是( ) A.内角和为360° B.对角线互相垂直 C.对边平行 D.对角线互相平分 △ABD, △BCD,△ABC,△ADC △ABO,△ADO,△BCO,△CDO 全等 B B A C D O 4 cm 6 cm 归纳:菱形中已知边长或对角线,求相关长度问题,一般 利用菱形的对角线垂直平分,再结合勾股定理解题. 已知菱形ABCD中,对角线AC、BD相交于点 O,AB=5cm,BD=8cm. 则:(1)BO=____________; (2)AC=_____________. 例1 如图,在菱形ABCD中,对角线AC与BD相交于点O, ∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长. 解:∵四边形ABCD是菱形, ∴AC⊥BD(菱形的对角线互相垂直), OB=OD= BD = ×6=3(菱形的对角线互相平分). 在等腰三角形ABC中, ∵∠BAD=60°, ∴△ABD是等边三角形. ∴AB = BD = 6. 1 2 1 2 A B C O D 例2 在RtΔAOB中,由勾股定理,得 OA2+OB2=AB2, ∴OA = = = ∴AC=2OA= (菱形的对角线相互平分). 2 2AB O B 2 26 3 3 3. 6 3 A B C O D 归纳:若菱形有一个内角为60°,那么60°角的两边与较 短的对角线可构成等边三角形,且两条对角线把菱形分成 四个全等的含30°角的直角三角形. 1.菱形具有而一般平行四边形不具有的性质是 ( ) A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等 2.如图,菱形的两条对角线长分别是6和8,则此菱形的 周长是 ( ) A.40 B.32 C.24 D.20 C D 3.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别 为BC,CD的中点,那么∠EAF的度数是 ( ) A.75° B.60° C.45° D.30° B FE C A B D 6.已知菱形的一条对角线与边长相等,则菱形的 四个内角度数分别为_____________________. 4.已知菱形的周长是12cm,那么它的边长是______. 5.菱形ABCD中∠ABC=120 °,则∠BAC=_______. A B C O D 3cm 30° 60°、60°、120°、120° 7.如图,在菱形ABCD中,对角线AC与BD 相交 于点O. 已知AB=5cm,AO=4cm,求BD的长. A B C O D 解:∵四边形ABCD是菱形, ∴AC⊥BD (菱形的两条对角线互相垂直), ∴∠AOB=90°, ∴BO= =3(cm), ∴BD=2BO=2×3=6(cm). 2 2AB AO 菱形的性质 菱形的性质 1.四边相等; 2.对角线互相垂直平分,且 每条对角线平分一组对角 菱形的定义 有一组邻边相等的平行四 边形是菱形查看更多