- 2021-05-28 发布 |
- 37.5 KB |
- 32页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学八年级下册同步课件-第19章 矩形、菱形与正方形-19正方形
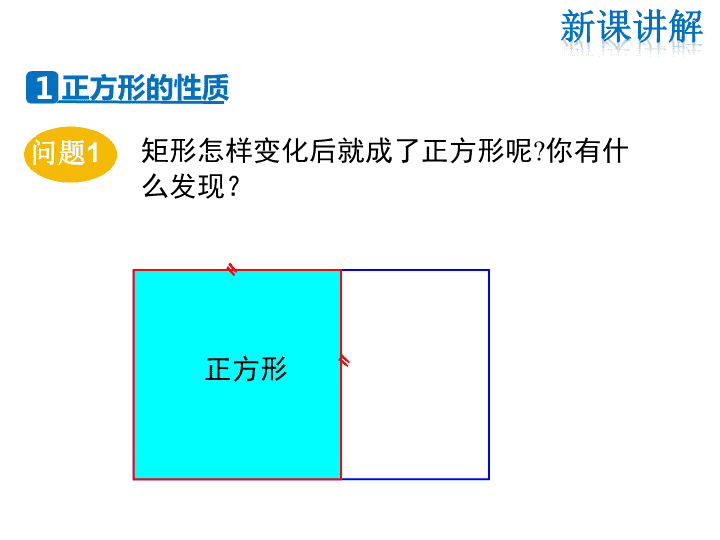
第19章 矩形、菱形与正方形 19.3 正方形 观察下面图形,正方形是我们熟悉的几何图形, 在生活中无处不在. 你还能举 出其他的 例子吗? 矩 形 〃 〃 矩形怎样变化后就成了正方形呢?你有什 么发现? 正方形 1 正方形的性质 问题1 正方形 菱形怎样变化后就成了正方形呢?你有什 么发现? 问题2 邻边相等矩形 〃 〃 正方形 〃 〃 菱 形 一个角是直角 正方形 ∟ 有一组邻边相等且有一个角是直角的平行四边 形叫正方形. ★正方形的定义 已知:如图,四边形ABCD是正方形. 求证:正方形ABCD四边相等,四个角都是直角. A B C D 证明:∵四边形ABCD是正方形. ∴∠A=90°, AB=AC (正方形的定义). 又∵正方形是平行四边形, ∴正方形是矩形(矩形的定义), 正方形是菱形(菱形的定义). ∴∠A=∠B =∠C =∠D = 90°, AB= BC=CD=AD. 证一证 已知:如图,四边形ABCD是正方形.对角线AC、BD 相交于点O.求证:AO=BO=CO=DO,AC⊥BD. A B C D O 证明:∵正方形ABCD是矩形, ∴AO=BO=CO=DO. ∵正方形ABCD是菱形. ∴AC⊥BD. 证一证 矩形 菱形 正 方 形 平行四边形 正方形是特殊的平行四边形,也是特殊的矩形,也是 特殊的菱形.所以矩形、菱形有的性质,正方形都有. 1.正方形的四个角都是直角,四条边相等. 2.正方形的对角线相等且互相垂直平分. ★正方形的性质 ★平行四边形、矩形、菱形、正方形之间的关系 由于正方形既是菱形,又是矩形,因此: 正方形是中心对称图形,对角线的交点是它 的对称中心. 正方形是轴对称图形,两条对角线所在 直线,以及过每一组对边中点的直线都是它 的对称轴. A B C D ★正方形的对称性 A D CB O 如图,四边形ABCD是正方形,对角线AC、BD相 交于点O. 求证: △ABO、 △BCO、 △CDO、 △DAO是全等的 等腰直角三角形. 证明: ∵ 四边形ABCD是正方形, ∴ AC=BD,AC⊥BD,AO=BO=CO=DO. ∴ △ABO、 △BCO、 △CDO、 △DAO都 是等腰直角三角形,并且 △ABO≌ △BCO ≌ △CDO ≌ △DAO. 例1 D A B C E 如图,在正方形ABCD中, ΔBEC是等边三角形. 求证: ∠EAD=∠EDA=15° . 证明:∵ ΔBEC是等边三角形, ∴BE=CE=BC,∠EBC=∠ECB=60°. ∵ 四边形ABCD是正方形, ∴AB=BC=CD,∠ABC=∠DCB=90°, ∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°, ∴△ABE、△DCE是等腰三角形, ∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°, ∴∠EAD= ∠EDA=90°-75°=15°. 例2 1.正方形具有而矩形不一定具有的性质是 ( ) A.四个角相等 B.对角线互相垂直平分 C.对角互补 D.对角线相等 2.正方形具有而菱形不一定具有的性质( ) A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等 B D 练一练 2.如图,四边形ABCD是正方形,对角线AC与BD 相交于点O,AO=2,求正方形的周长与面积. 解:∵四边形ABCD是正方形, ∴AC⊥BD,OA=OD=2. 在Rt△AOD中,由勾股定理,得 ∴正方形的周长为4AD= , 面积为AD2=8. 2 2 2 2,AD AO OD 8 2 准备一张矩形的纸片,按照下图折叠,然后展开, 折叠部分得到一个正方形,可量一量验证验证. 正方形 猜想:满足怎样条件的矩形是正方形? 矩形 正方 形 一组邻边相等 对角线互相垂直 2 正方形的判定 活动1 已知:如图,在矩形ABCD中,AC , DB是它的两条对角线, AC⊥DB. 求证:四边形ABCD是正方形. 证明:∵四边形ABCD是矩形, ∴ AO=CO=BO=DO . ∵AC⊥DB, ∴ AD=AB=BC=CD, ∴矩形ABCD是正方形. A B CD O 求证:对角线互相垂直的矩形是正方形. 证一证 把可以活动的菱形框架的一个角变为直角,观 察这时菱形框架的形状.量量看是不是正方形. 正方形 菱形 猜想 :满足怎样条件的菱形是正方形? 正方 形 一个角是直角 对角线相等 活动2 已知:如图,在菱形ABCD中,AC , DB是它的两条对角线, AC=DB. 求证:四边形ABCD是正方形. 证明:∵四边形ABCD是菱形, ∴AB=BC=CD=AD,AC⊥DB. ∵AC=DB, ∴ AO=BO=CO=DO, ∴△AOD,△AOB,△COD,△BOC是等腰直角三角形, ∴∠DAB=∠ABC=∠BCD=∠ADC=90°, ∴菱形ABCD是正方形. A B CD O 求证:对角线相等的菱形是正方形. 证一证 正方形判定的几条途径: 正方形 正方形 + + 先判定菱形 先判定矩形 矩形条件(二选一) 菱形条件(二选一) 一个直角或 一组邻边相等 对角线相等 或对角线垂直 平行四 边形 正方形一组邻边相等 且一内角是直角 ★正方形的判定 在四边形ABCD中,O是对角线的交点,能判 定这个四边形是正方形的是( ) A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC C A B CD O 练一练 在正方形ABCD中,点E、F、M、N分别在各边 上,且AE=BF=CM=DN.四边形EFMN是正方形吗? 为什么? 解答:∵四边形ABCD是正方形, ∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°. ∵AE=BF=CM=DN, ∴AN=BE=CF=DM. 分析:由已知可证△AEN≌△BFE≌ △CMF≌△DNM,得四边形EFMN 是菱形,再证有一个角是直角即可. 例3 在△AEN、△BFE、△CMF、△DNM中, AE=BF=CM=DN, ∠A=∠B=∠C=∠D, AN=BE=CF=DM, ∴△AEN≌△BFE≌△CMF≌△DNM, ∴EN=FE=MF=NM,∠ANE=∠BEF, ∴四边形EFMN是菱形, ∠NEF=180°-(∠AEN+∠BEF) =180°-(∠AEN+∠ANE) =180°-90°=90°. ∴四边形EFMN是正方形 . 证明:∵ DE⊥AC,DF⊥AB , ∴∠DEC= ∠DFC=90°. 又∵ ∠C=90 °, ∴四边形EDFC是矩形. 过点D作DG⊥AB,垂足为G. ∵AD是∠CAB的平分线 DE⊥AC,DG⊥AB, ∴ DE=DG. 同理得DG=DF,∴ED=DF, ∴矩形EDFC是正方形. 如图,在直角三角形中,∠C=90°,∠A、∠B的 平分线交于点D.DE⊥AC,DF⊥AB. 求证:四边形CEDF为正方形. A B C D E F G 例4 如图,正方形ABCD,动点E在AC上,AF⊥AC, 垂足为A,AF=AE. (1)求证:BF=DE; (2)当点E运动到AC中点时(其他条件都保持不变), 问四边形AFBE是什么特殊四边形?说明理由. (1)证明:∵正方形ABCD, ∴AB=AD,∠BAD=90°, ∵AF⊥AC,∴∠EAF=90°, ∴∠BAF=∠EAD, 在△ADE和△ABF中, AD=AB ,∠DAE=∠BAF ,AE=AF , ∴△ADE≌△ABF(SAS),∴BF=DE. 例5 (2)解:当点E运动到AC的中点时四边 形AFBE是正方形, 理由:∵点E运动到AC的中点,AB=BC, ∴BE⊥AC,BE=AE= AC, ∵AF=AE, ∴BE=AF=AE. 又∵BE⊥AC,∠FAE=∠BEC=90°, ∴BE∥AF, ∵BE=AF, ∴四边形AFBE为平行四边形, ∵∠FAE=90°,AF=AE, ∴平行四边形AFBE是正方形. 1 2 2.一个正方形的对角线长为2cm,则它的面积是 ( ) A.2cm2 B.4cm2 C.6cm2 D.8cm2 A 1.平行四边形、矩形、菱形、正方形都具有的是( ) A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.对角线互相垂直且相等 A 3.在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= . 4.在正方形ABCD中,E是对角线AC上一点,且AE=AB, 则∠EBC的度数是 . A D B C O A D B C O E 45° 90° 22.5° 第3题 第4题 45° 5.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA =90°,请添加一个条件____________________, 可得出该四边形是正方形. AB=BC(答案不唯一) A B CD O 6.已知四边形ABCD是平行四边形,再从①AB=BC, ②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中, 选两个作为补充条件后,使得四边形ABCD是正方形, 其中错误的是_________________(只填写序号).②③(答案不唯一) 7.如图,正方形ABCD的边长为1cm,AC为对角线, AE平分∠BAC,EF⊥AC,求BE的长. 解:∵四边形ABCD为正方形, ∴∠B=90°,∠ACB=45°,AB=BC=1cm. ∵EF⊥AC,∴∠EFA=∠EFC=90°. 又∵∠ECF=45°, ∴△EFC是等腰直角三角形,∴EF=FC. ∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE, ∴△ABE≌△AFE, ∴AB=AF=1cm,BE=EF. ∴FC=BE. 在Rt△ABC中, ∴FC=AC-AF=( -1)cm, ∴BE=( -1)cm. 2 2 2cm,AC AB BC 2 2 8. 如图,在正方形ABCD中,E为CD上一点,F为BC边 延长线上一点,且CE=CF. BE与DF之间有怎样的关 系?请说明理由. 解:BE=DF,且BE⊥DF.理由如下: ∵四边形ABCD是正方形. ∴BC=DC,∠BCE =90° . ∴∠DCF=180°-∠BCE=90°. ∴∠BCE=∠DCF. 又∵CE=CF. ∴△BCE≌△DCF. ∴BE=DF. A B D C F E 延长BE交DF于点M, ∵△BCE≌△DCF , ∴∠CBE =∠CDF. ∵∠DCF =90° , ∴∠CDF +∠F =90°, ∴∠CBE+∠F=90° , ∴∠BMF=90°. ∴BE⊥DF. A B D F E C M 1.四个角都是直角 2.四条边都相等 3.对角线相等且互相垂直平分 正方形 的性质 性质 定义 有一组邻相等,并且有一个角是 直角的平行四边形叫做正方形. 5种判 定方法 三个角是直角 四条边相等 一 个 角 是 直 角 或 对 角 线 相 等 一组邻边相等 或对角线垂直 一组邻边相等 或对角线垂直 一个角是直角 或对角线相等 一个角是直角且一组邻边相等 ★平行四边形、矩形、菱形、正方形的判定小结查看更多