- 2021-05-27 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
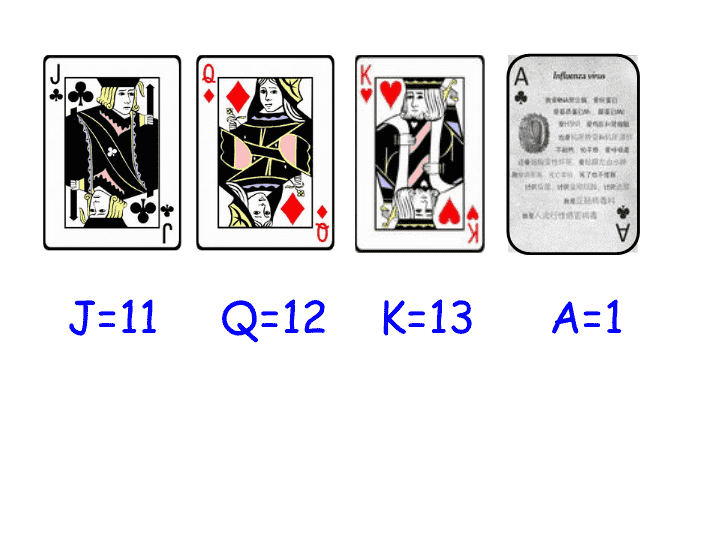
五年级上册数学课件-4 简易方程(用字母表示数)▏沪教版 (13)
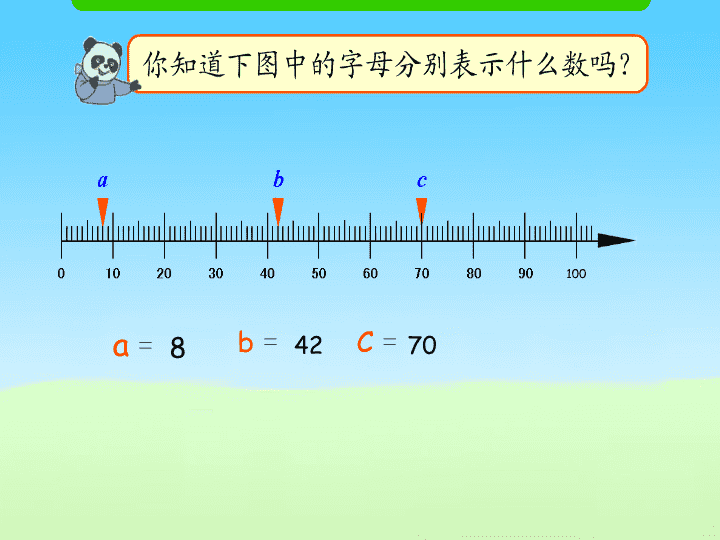
用字母表示数 J=11 Q=12 K=13 A=1 100 a = b = C = 8 42 70 3 6 9 12 x 18 21 y 27 z 33 … x = 15 y = 24 z =30 找规律 , 说说下列字母表示哪些数 ? 这些字母式子你们认识吗? a- b-c =a-( b+c ) a+b = b+a ( a+b)+c = a+(b+c ) a×b = b×a ( a×b ) ×c=a× ( b×c ) ( a+b)×c = a×c+b×c a÷b÷c = a÷(b×c ) (b≠0,c≠0) a÷b =(a × c) ÷(b × c) (b≠0,c≠0) 乘法交换律 乘法分配律 除法的运算性质 加法交换律 加法结合律 减法的运算性质 乘法结合律 商不变性质 表一: 运算定律 字母式子 加法交换律 加法结合律 乘法交换律 乘法结合律 乘法分配律 a+b = b+a ( a+b)+c = a+(b+c ) a×b = b×a ( a×b)×c=a×( b×c ) ( a+b)×c = a×c+b×c 表二: 运算性质 字母式子 减法的运算性质 除法的运算性质 商不变性质 a- b-c =a-( b+c ) a÷b÷c = a÷(b×c ) (b≠0,c≠0) a÷b =(a × c) ÷(b × c) (b≠0,c≠0) 学习任务一: 自学书本第 41 页例 2 , 想一想 在什么情况下 哪个运算符号可以 记作“ ·” 或 省略不写 ? 请你和同伴一起 试一试 简写这些字母式子。 找一找 表一 和 表二 里哪些字母式子可以进行 简写? 正方形的周长 正方形的面积 a = (长 + 宽) × 2 长方形的面积 a b 长方形的周长 = 边长 ×4 = 长 × 宽 = 边长 × 边长 c c s s = (a+b)×2 = a×4 = a×b = a×a 学习任务二: 自学书本第 42 页例 3 , 想一想 在什么情况下 哪个运算符号可以 记作“ ·” 或 省略不写 ? 在简写时应 注意什么? 还有哪些 特殊 情况? 表三: 计算公式 字母公式 记作“ · ” 省略不写 长方形的周长 C=(a+b) ×2 正方形的周长 C=a ×4 长方形的面积 S=a ×b 正方形的面积 S=a ×a 小小辩论会 一、在字母式子里,“ + 、 - 、 ÷” 可以记作“ ·” 或省略不写吗? 二、在数字与数字之间可以把乘号记作“ ·” 或 省略不写吗? ( 1 ) x×y = x · y ( 4 ) v÷ t = v ·t = xy = v t 判断:下列式子这样表示正确吗? = 34 ( 2 ) 3×4 = 3 · 4 √ √ ( 3 ) m+n = m · n = mn ( 5 ) b×b = b · b = b 2 简写下列字母式子。 (1)y×1.3= ( 2)b×1= (3)7×a + 8×b= (4)a×b×6= (5) a×1 + b×3= (6)a×b÷6= 想一想:下面的字母式子怎样简写? (1)c×c = (2) c+c = c 2 2 c 选择: (1) ( a+b ) ×5 可以写成 …………… ( ) ① ( a+b ) 5 ② 5(ab ) ③ 5(a+b) (2) 与 2b 不相等的算式是 ………… ( ) ① b×2 ② b 2 ③ b+b ③ ② 不足之处,请指正。 表一: 运算定律 字母式子 记作“ · ” 省略不写 加法交换律 加法结合律 乘法交换律 乘法结合律 乘法分配律 a+b = b+a ( a+b)+c = a+(b+c ) a×b = b×a ( a×b)×c=a×( b×c ) ( a+b)×c = a×c+b×c a · b=b · a ab=ba 表二: 运算性质 字母式子 记作“ · ” 省略不写 减法的运算性质 除法的运算性质 商不变性质 a- b-c =a-( b+c ) a÷b÷c = a÷(b×c ) (b≠0,c≠0) a÷b =(a × c) ÷(b × c) (b≠0,c≠0)查看更多