- 2021-05-27 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教B版第45讲椭圆学案
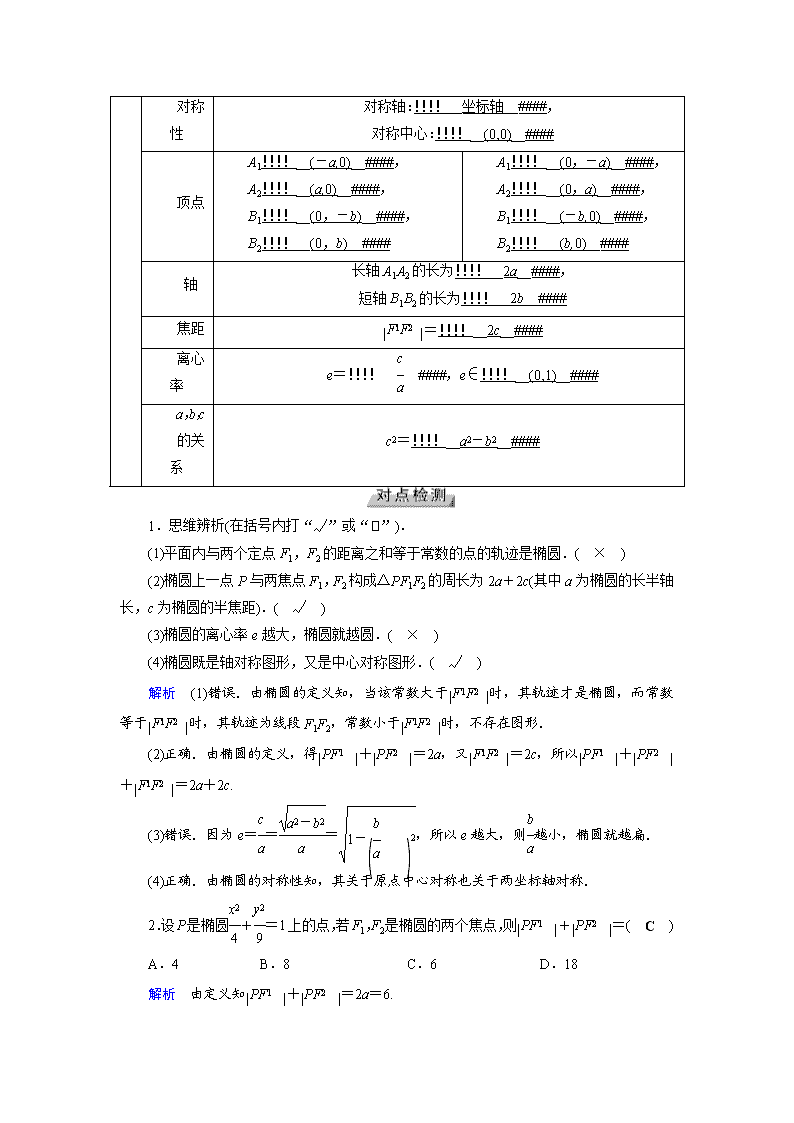
第45讲 椭 圆 考纲要求 考情分析 命题趋势 1.掌握椭圆的定义、几何图形、标准方程及简单几何性质. 2.了解圆锥曲线的简单应用,了解椭圆的实际背景. 3.理解数形结合的思想. 2017·全国卷Ⅱ,20 2016·全国卷Ⅲ,11 2016·天津卷,20 1.求解与椭圆定义有关的问题;利用椭圆的定义求轨迹方程;求椭圆的标准方程;判断椭圆焦点的位置. 2.求解与椭圆的范围、对称性有关的问题;求解椭圆的离心率;求解与椭圆的焦点三角形有关的问题. 分值:5~12分 1.椭圆的定义 平面内与两个定点F1,F2的距离之和等于常数(大于)的点的轨迹叫做!!!!__椭圆__####.这两个定点叫做椭圆的!!!!__焦点__####,两焦点间的距离叫做椭圆的!!!!__焦距__####. 集合P={M|+=2a},=2c,其中a>0,c>0,且a,c为常数. (1)若!!!!__a>c__####,则集合P为椭圆; (2)若!!!!__a=c__####,则集合P为线段; (3)若!!!!__a<c__####,则集合P为空集. 2.椭圆的标准方程和几何性质 标准方程 +=1(a>b>0) +=1(a>b>0) 图形 性 质 范围 !!!!__-a__####≤x≤!!!!__a__####, !!!!__-b__####≤y≤!!!!__b__#### !!!!__-b__####≤x≤!!!!__b__####, !!!!__-a__####≤y≤!!!!__a__#### 对称 对称轴:!!!!__坐标轴__####, 性 对称中心:!!!!__(0,0)__#### 顶点 A1!!!!__(-a,0)__####, A2!!!!__(a,0)__####, B1!!!!__(0,-b)__####, B2!!!!__(0,b)__#### A1!!!!__(0,-a)__####, A2!!!!__(0,a)__####, B1!!!!__(-b,0)__####, B2!!!!__(b,0)__#### 轴 长轴A1A2的长为!!!!__2a__####, 短轴B1B2的长为!!!!__2b__#### 焦距 =!!!!__2c__#### 离心率 e=!!!! ####,e∈!!!!__(0,1)__#### a,b,c 的关系 c2=!!!!__a2-b2__#### 1.思维辨析(在括号内打“√”或“”). (1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆.( × ) (2)椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c(其中a为椭圆的长半轴长,c为椭圆的半焦距).( √ ) (3)椭圆的离心率e越大,椭圆就越圆.( × ) (4)椭圆既是轴对称图形,又是中心对称图形.( √ ) 解析 (1)错误.由椭圆的定义知,当该常数大于时,其轨迹才是椭圆,而常数等于时,其轨迹为线段F1F2,常数小于时,不存在图形. (2)正确.由椭圆的定义,得+=2a,又=2c,所以++=2a+2c. (3)错误.因为e===,所以e越大,则越小,椭圆就越扁. (4)正确.由椭圆的对称性知,其关于原点中心对称也关于两坐标轴对称. 2.设P是椭圆+=1上的点,若F1,F2是椭圆的两个焦点,则+=( C ) A.4 B.8 C.6 D.18 解析 由定义知+=2a=6. 3.若方程+=1表示椭圆,则m的范围是( C ) A.(-3,5) B.(-5,3) C.(-3,1)∪(1,5) D.(-5,1)∪(1,3) 解析 由方程表示椭圆知 解得-3<m<5且m≠1. 4.(2018·广东惠州二调)设F1,F2为椭圆+=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则的值为( D ) A. B. C. D. 解析 如图,设线段PF1的中点为M,因为O是F1F2的中点,所以OM∥PF2,可得PF2⊥x轴,|PF2|==,|PF1|=2a-|PF2|=,=.故选D. 5.已知F1,F2是椭圆C的左、右焦点,点P在椭圆上,且满足=2,∠PF1F2=30°,则椭圆的离心率为!!!!____####. 解析 在△PF1F2中,由正弦定理得sin∠PF2F1=1,即∠PF2F1=.设=1,则=2,=,所以离心率e==. 一 椭圆的定义及应用 椭圆定义的应用主要有两个方面:一是确认平面内与两定点有关的轨迹是否为椭圆;二是当P在椭圆上时,与椭圆的两焦点F1,F2组成的三角形通常称为“焦点三角形”,利用定义可求其周长,利用定义和余弦定理可求·,通过整体代入可求其面积等. 【例1】 (1)如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( A ) A.椭圆 B.双曲线 C.抛物线 D.圆 (2)已知F1,F2是椭圆C:+=1(a>b>0)的两个焦点,P为椭圆C上的一点,且⊥.若△PF1F2的面积为9,则b=!!!!__3__####. 解析 (1)由折叠过程可知点M与点F关于直线CD对称,故=,所以+=+==r, 由椭圆的定义可知,点P的轨迹为椭圆. (2)设=r1,=r2,则 ∴2r1r2=(r1+r2)2-(r+r)=4a2-4c2=4b2. 又∵S△PF1F2=r1r2=b2=9,∴b=3. 二 椭圆的标准方程 求椭圆的标准方程的方法 求椭圆标准方程的基本方法是待定系数法,具体过程是先定形,再定量,即首先确定焦点所在位置,然后再根据条件建立关于a,b的方程组.如果焦点位置不确定,要考虑是否有两解,有时为了解题方便,也可把椭圆方程设为mx2+ny2=1(m>0,n>0,m≠n)的形式. 【例2】 求满足下列条件的椭圆的标准方程. (1)过点(,-),且与椭圆+=1有相同的焦点; (2)已知点P在以坐标轴为对称轴的椭圆上,且P到两焦点的距离分别为5,3,过P且与长轴垂直的直线恰过椭圆的一个焦点; (3)经过两点,(,). 解析 (1)椭圆+=1的焦点为(0,-4),(0,4),即c=4. 由椭圆的定义知, 2a=+, 解得a=2. 由c2=a2-b2可得b2=4. 所以所求椭圆的标准方程为+=1. (2)由于焦点的位置不确定,∴设所求的椭圆方程为+=1(a>b>0)或+=1(a>b>0). 由已知条件得解得a=4,c=2,∴b2=12. 故椭圆方程为+=1或+=1. (3)设椭圆方程为mx2+ny2=1(m,n>0,m≠n), 由解得m=,n=. ∴椭圆方程为+=1. 三 椭圆的几何性质 求椭圆离心率的方法 (1)直接求出a,c,从而求解e,通过已知条件列方程组,解出a,c的值. (2)构造a,c的齐次式,解出e,由已知条件得出a,c的二元齐次方程,然后转化为关于离心率e的一元二次方程求解. (3)通过特殊值或特殊位置,求出离心率. 【例3】 (1)椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,A,B是C上两点,=3,∠BAF2=90°,则椭圆C的离心率为( D ) A. B. C. D. (2)已知F1(-c,0),F2 (c,0)为椭圆+=1的两个焦点,P在椭圆+=1上,且满足·=c2,则此椭圆离心率的取值范围是( C ) A. B. C. D. 解析 (1)由条件=3,设||=x,则||=3x.在△ABF2中,有(4x)2+(2a-3x)2=(2a-x)2,整理得x(3x-a)=0,即3x=a,x=,在Rt△AF1F2中,有=2c,(3x)2+(2a-3x)2=4c2.将x=代入,得a2+(2a-a)2=4c2,解得=,即e=. (2)由椭圆的定义得+=2a,平方得2+2+2·=4a2.① 又∵·=c2,∴·cos∠F1PF2=c2.② 由余弦定理得2+2-2··cos∠F1PF2=2=4c2.③ 由①②③,得cos∠F1PF2=. 又∵0<cos∠F1PF2≤1,∴e≤. ∵·≤2=a2, ∴2a2-3c2≤a2,a2≤3c2,e≥,则此椭圆离心率的取值范围是.故选C. 四 直线与椭圆的综合问题 直线与椭圆综合问题的常见题型及解题策略 (1)求直线方程.可依题设条件,寻找确定该直线的两个条件,进而得到直线方程. (2)求面积.先确定图形的形状,再利用条件寻找确定面积的条件,进而得出面积的值. (3)判断图形的形状.可依据平行、垂直的条件判断边角关系,再依据距离公式得出边之间的关系. (4)弦长问题.利用根与系数的关系、弦长公式求解. (5)中点弦或弦的中点.一般利用点差法求解,注意判断直线与椭圆是否相交. 【例4】 (2017·全国卷Ⅱ)设O为坐标原点,动点M在椭圆C:+y2=1上,过M作x轴的垂线,垂足为N,点P满足= . (1)求点P的轨迹方程; (2)设点Q在直线x=-3上,且·=1.证明:过点P且垂直于OQ的直线l过C的左焦点F. 解析 (1)设P(x,y),M(x0,y0),则N(x0,0),=(x-x0,y),=(0,y0). 由= ,得x0=x,y0=y. 因为M(x0,y0)在C上,所以+=1. 因此点P的轨迹方程为x2+y2=2. (2)由题意知F(-1,0).设Q(-3,t),P(m,n),则 =(-3,t),=(-1-m,-n),·=3+3m-tn, =(m,n),=(-3-m,t-n), 由·=1,得-3m-m2+tn-n2=1,又由(1)知m2+n2=2,故3+3m-tn=0. 所以·=0,即⊥,又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F. 【例5】 已知椭圆+=1(a>b>0)的一个顶点为B(0,4),离心率e=,直线l交椭圆于M,N两点. (1)若直线l的方程为y=x-4,求弦|MN|的长; (2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l方程的一般式. 解析 (1)由已知得b=4,且=,即=, ∴=,解得a2=20, ∴椭圆方程为+=1. 将4x2+5y2=80与y=x-4联立, 消去y得9x2-40x=0, ∴x1=0,x2=, ∴所求弦长|MN|=|x2-x1|=. (2)椭圆右焦点F的坐标为(2,0),设线段MN的中点为Q(x0,y0), 由三角形重心的性质知B=2F, 又B(0,4),∴(2,-4)=2(x0-2,y0), 故得x0=3,y0=-2, 即Q的坐标为(3,-2). 设M(x1,y1),N(x2,y2), 则x1+x2=6,y1+y2=-4, 且+=1,+=1, 以上两式相减得+=0, ∴kMN==-·=-×=, 故直线MN的方程为y+2=(x-3), 即6x-5y-28=0. 1.(2017·浙江卷)椭圆+=1的离心率是( B ) A. B. C. D. 解析 根据题意知a=3,b=2,则c==,∴椭圆的离心率e==.故选B. 2.(2017·全国卷Ⅲ)已知椭圆C:+=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为( A ) A. B. C. D. 解析 以线段A1A2为直径的圆的圆心为坐标原点O(0,0),半径为a,由题意,圆心到直线bx-ay+2ab=0的距离为=a,即a2=3b2.又e2=1-=,所以e=.故选A. 3.(2017·全国卷Ⅰ)设A,B是椭圆C:+=1长轴的两个端点.若C上存在点M满足∠AMB=120°,则m的取值范围是( A ) A.(0,1]∪[9,+∞) B.(0,]∪[9,+∞) C.(0,1]∪[4,+∞) D.(0,]∪[4,+∞) 解析 依题意得或 所以或解得0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档