陕西省安康市2021届高三10月联考试题 数学(文) Word版含答案
www.ks5u.com
绝密★启用前
2020~2021学年第一学期高三10月阶段性考试
文科数学
本试卷共4页。全卷满分150分,考试时间120分钟。
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|4-x2>0},B={x|0
0,|φ|<)的部分图像如图所示,则下列结论正确的是
A.x=-是f(x)图像的一条对称轴
B.f(x)图像的对称中心为(2kπ+,0),k∈Z
C.f(x)≥1的解集为[4kπ,4kπ+],k∈Z
D.f(x)的单调递减区间为[2kπ+,2kπ+],k∈Z
12.已知a,b,c分别为△ABC内角A,B,C的对边,bsinC=2c·cosB,b=,则当△ABC的周长最大时,△ABC的面积为
A. B. C. D.3
二、填空题:本题共4小题,每小题5分,共20分。
- 9 -
13.已知等比数列{an}的公比为2,Sn为其前n项和,则当= 。
14.若函数f(x)=与g(x)=ex-a-b的图像在x=1处有相同的切线,则a+b= 。
15.将函数f(x)=cos(x-)的图像上各点的横坐标缩短到原来的倍(纵坐标不变),再把得到的图像向左平移个单位长度得到函数g(x)的图像,则g(x)在区间[-,]上的值域为 。
16.已知函数f(x)=log3+b,若f(a)=1,f(-a)=3,则logba= 。
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
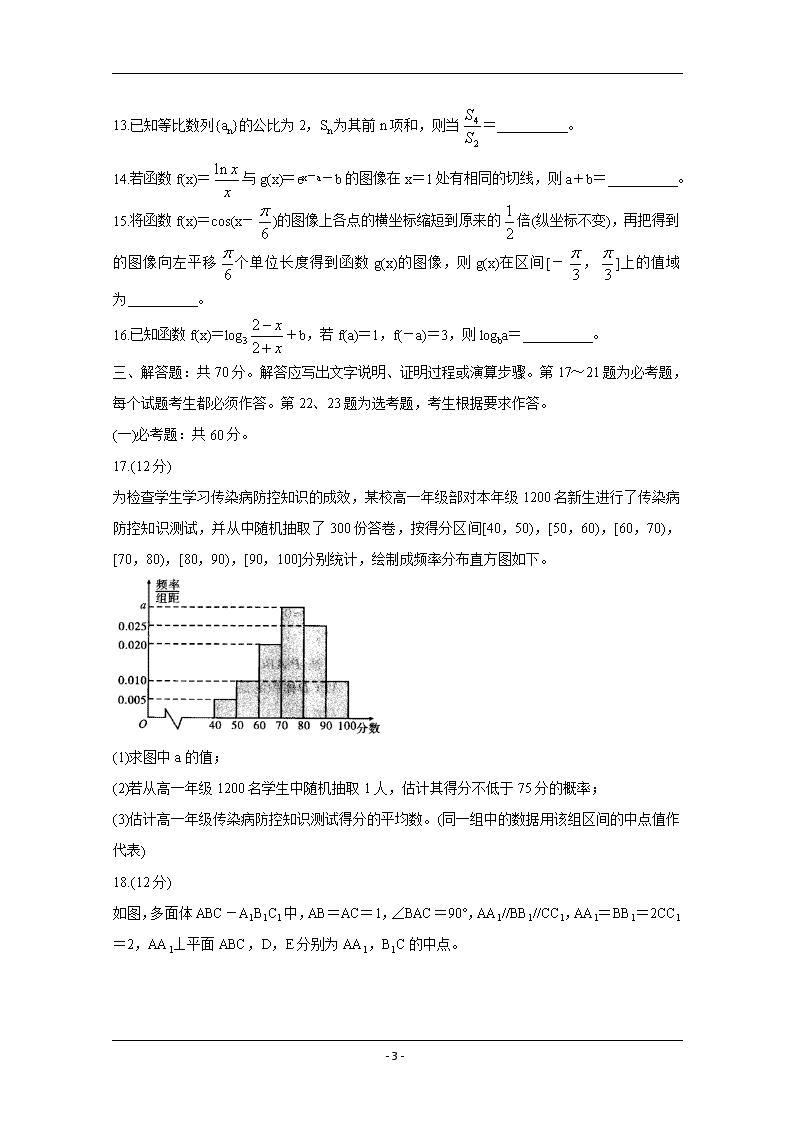
为检查学生学习传染病防控知识的成效,某校高一年级部对本年级1200名新生进行了传染病防控知识测试,并从中随机抽取了300份答卷,按得分区间[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分别统计,绘制成频率分布直方图如下。
(1)求图中a的值;
(2)若从高一年级1200名学生中随机抽取1人,估计其得分不低于75分的概率;
(3)估计高一年级传染病防控知识测试得分的平均数。(同一组中的数据用该组区间的中点值作代表)
18.(12分)
如图,多面体ABC-A1B1C1中,AB=AC=1,∠BAC=90°,AA1//BB1//CC1,AA1=BB1=2CC1=2,AA1⊥平面ABC,D,E分别为AA1,B1C的中点。
- 9 -
(1)证明:DE//平面ABC;
(2)求平面B1CD将多面体ABC-A1B1C1分成上、下两部分的体积比。
19.(12分)
已知a,b,c分别为△ABC内角A,B,C的对边,sinA=,cosB=。
(1)证明:a:b:c=3:5:7;
(2)若||=,求△ABC的面积。
20.(12分)
已知直线l:y=kx+1过抛物线E:x2=2py(p>0)的焦点,且与E交于A,B两点。
(1)求抛物线E的方程;
(2)以AB为直径的圆与x轴交于C,D两点,若|CD|≥4,求k的取值范围。
21.(12分)
已知函数f(x)=ex-ax。
(1)讨论f(x)的单调性;
(2)当x>-1时,f(x)>a(x2+x),求a的取值范围。
(二)选考题:共10分。请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
以直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系。已知曲线C1:ρ=4sin(θ+),M是C1上的动点,点N在射线OM上且满足2ON=OM,设点N的轨迹为C2。
(1)写出曲线C2的极坐标方程,并化为直角坐标方程;
(2)已知直线l的参数方程为(t为参数,0≤φ<π),曲线C2截直线l
- 9 -
所得线段的中点坐标为(),求φ的值。
23.[选修4-5:不等式选讲](10分)
已知函数f(x)=|x+3|-|x-1|。
(1)在坐标系中画出函数y=f(x)的图像,并写出f(x)的值域;
(2)若f(x)≤|x+a|恒成立,求a的取值范围。
- 9 -
- 9 -
- 9 -
- 9 -
- 9 -