【数学】2018届一轮复习人教A版函数的图象教案

【数学】2018届一轮复习人教A版函数的图象教案

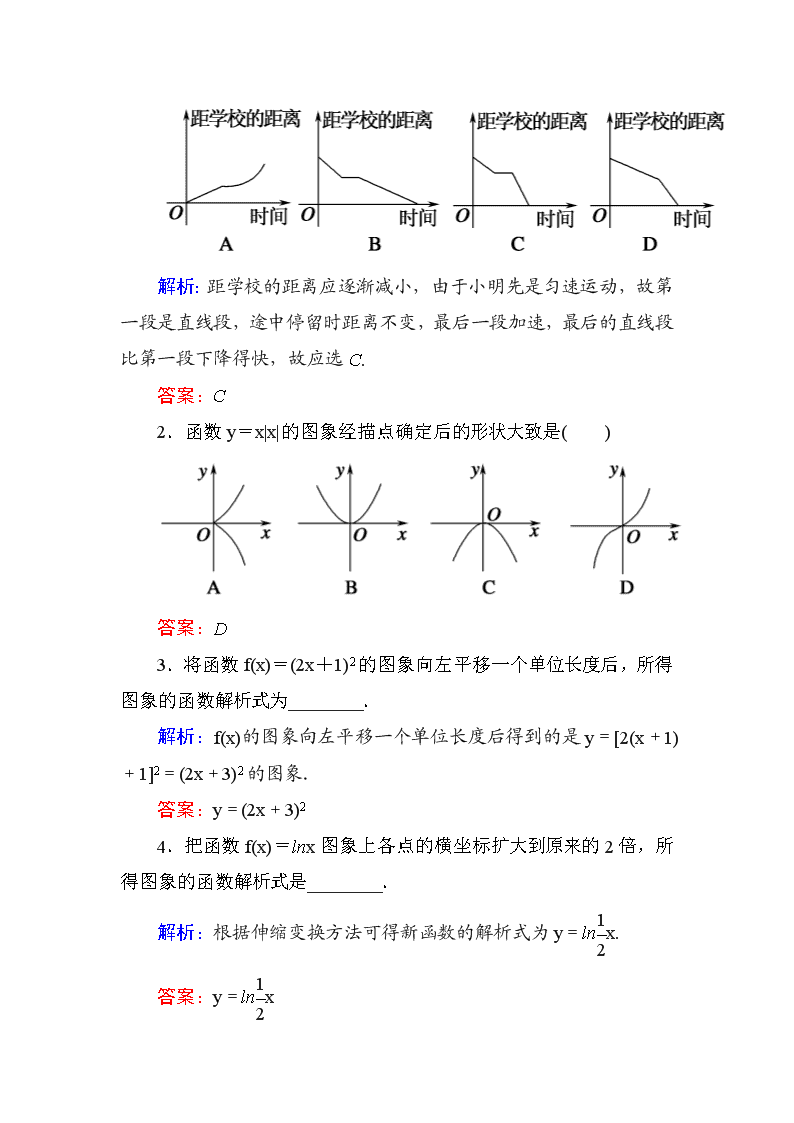
‎　‎ ‎1.掌握基本初等函数的图象特征，能熟练运用基本初等函数的图象解决问题．‎ ‎2．掌握图象的作法：描点法和图象变换．‎ ‎3．会运用函数的图象理解和研究函数的性质．‎ 知识点一　利用描点法作函数图象 ‎ 其基本步骤是列表、描点、连线，首先：①确定函数的定义域；②化简函数________；③讨论函数的性质(______________________)；其次：列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点)；最后：描点，连线．‎ 答案 ‎②解析式　③奇偶性、单调性、周期性 知识点二　利用基本函数的图象作图 ‎ ‎1．平移变换 ‎(1)水平平移：y＝f(x±a)(a>0)的图象，可由y＝f(x)的图象向____(＋)或向____(－)平移____单位而得到．‎ ‎(2)竖直平移：y＝f(x)±b(b>0)的图象，可由y＝f(x)的图象向____(＋)或向____(－)平移____单位而得到．‎ ‎2．对称变换 ‎(1)y＝f(－x)与y＝f(x)的图象关于____对称．‎ ‎(2)y＝－f(x)与y＝f(x)的图象关于____对称．‎ ‎(3)y＝－f(－x)与y＝f(x)的图象关于____对称．‎ ‎(4)要得到y＝|f(x)|的图象，可将y＝f(x)的图象在x轴下方的部分以____为对称轴翻折到x轴上方，其余部分不变．‎ ‎(5)要得到y＝f(|x|)的图象，可将y＝f(x)，x≥0的部分作出，再利用偶函数的图象关于____的对称性，作出x<0时的图象．‎ ‎3．伸缩变换 ‎(1)y＝Af(x)(A>0)的图象，可将y＝f(x)图象上所有点的纵坐标变为__________，________不变而得到．‎ ‎(2)y＝f(ax)(a>0)的图象，可将y＝f(x)图象上所有点的横坐标变为__________，________不变而得到．‎ 答案 ‎1．(1)左　右　a个　(2)上　下　b个 ‎2．(1)y轴　(2)x轴　(3)原点　(4)x轴　(5)y轴 ‎3．(1)原来的A倍　横坐标　(2)原来的倍　纵坐标 ‎1．(必修①P‎112A组第4题改编)小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶．与以上事件吻合得最好的图象是(　　)‎ 解析：距学校的距离应逐渐减小，由于小明先是匀速运动，故第一段是直线段，途中停留时距离不变，最后一段加速，最后的直线段比第一段下降得快，故应选C.‎ 答案：C ‎2．函数y＝x|x|的图象经描点确定后的形状大致是(　　)‎ 答案：D ‎3．将函数f(x)＝(2x＋1)2的图象向左平移一个单位长度后，所得图象的函数解析式为________．‎ 解析：f(x)的图象向左平移一个单位长度后得到的是y＝[2(x＋1)＋1]2＝(2x＋3)2的图象．‎ 答案：y＝(2x＋3)2‎ ‎4．把函数f(x)＝lnx图象上各点的横坐标扩大到原来的2倍，所得图象的函数解析式是________．‎ 解析：根据伸缩变换方法可得新函数的解析式为y＝lnx.‎ 答案：y＝lnx ‎5．若关于x的方程|x|＝a－x只有一个解，则实数a的取值范围是________．‎ 解析：在同一直角坐标系中，画出函数y＝|x|和函数y＝－x＋a的图象，即可知当a>0时，两函数有且只有一个交点，即|x|＝a－x只有一个解．‎ 答案：(0，＋∞)‎ 热点一 　作函数的图象 ‎ ‎【例1】　作出下列函数的图象：‎ ‎(1)y＝elnx；‎ ‎(2)y＝|log2(x＋1)|；‎ ‎(3)y＝a|x|(00}，且y＝elnx＝x(x>0)，‎ 所以其图象如图(1)所示．‎ ‎(2)将函数y＝log2x的图象向左平移一个单位，再将x轴下方的部分沿x轴翻折上去，即可得到函数y＝|log2(x＋1)|的图象，如图(2)所示．‎ ‎(3)因为y＝(00，‎ 解得x>1或－10，‎ 在上y＝cosx<0.‎ 由f(x)的图象知在上<0，‎ 因为f(x)为偶函数，y＝cosx也是偶函数，‎ 所以y＝为偶函数，‎ 所以<0的解集为∪.‎ ‎【答案】　∪ 考向4　利用图象求参数取值范围 ‎【例6】　(2016·山东卷)已知函数f(x)＝‎ 其中m>0.若存在实数b，使得关于x的方程f(x)＝b有三个不同的根，则m的取值范围是________．‎ ‎【解析】　f(x)＝当x>m时，f(x)＝x2－2mx＋‎4m＝(x－m)2＋‎4m－m2，其顶点为(m,‎4m－m2)；当x≤m时，函数f(x)的图象与直线x＝m的交点为Q(m，m)．①当即03时，函数f(x)的图象如图2所示，则存在实数b满足‎4m－m20时，f(x)是周期函数，如图，‎ 欲使方程f(x)＝x＋a有两解，即函数f(x)的图象与直线y＝x＋a有两个不同交点，故a<1，则a的取值范围是(－∞，1)．‎ 答案：(1)C　(2)(－∞，1)‎ ‎1．列表描点法是作函数图象的辅助手段，要作函数图象首先要明确函数图象的位置和形状 ‎(1)可通过研究函数的性质如定义域、值域、奇偶性、周期性、单调性等；‎ ‎(2)可通过函数图象的变换如平移变换、对称变换、伸缩变换等；‎ ‎(3)可通过方程的同解变形，如作函数y＝的图象．‎ ‎2．合理处理识图题与用图题 ‎(1)识图 对于给定函数的图象，要从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性，注意图象与函数解析式中参数的关系．‎ ‎(2)用图 要用函数的思想指导解题，即方程的问题函数解(方程的根即相应函数图象与x轴交点的横坐标，或是方程变形后，等式两端相对应的两函数图象交点的横坐标)，不等式的问题函数解(不等式的解集即一个函数图象在另一个函数图象的上方或下方时的相应x的范围)．‎ ‎“形似神异”的图象变换规律 在函数图象变换中，与对数函数图象相关的变换，有许多结构形式类似，稍不注意，就会出现差错．常用的几个变换如下：‎ ‎(1)y＝logax→y＝|loga(x－m)|＋n(其中m>0，n>0)：‎ y＝logax y＝|logax| y＝|loga(x－m)| y＝|loga(x－m)|＋n；‎ ‎(2)y＝logax→y＝loga|x－m|＋n：‎ y＝logax y＝loga|x| y＝loga|x－m| y＝loga|x－m|＋n；‎ ‎(3)y＝logax→y＝loga(|x－m|＋n)：‎ y＝logax图象向左平移n个单位长度,y＝loga(x＋n)‎ y＝loga(|x|＋n) y＝loga(|x－m|＋n)；‎ ‎(4)y＝logax→y＝|loga|x－m||：‎ y＝logax y＝|logax| y＝|loga|x|| y＝|loga|x－m||.‎ ‎【例】　对于函数f(x)＝lg(|x－2|＋1)，给出如下三个命题：①f(x＋2)是偶函数；②f(x)在区间(－∞，2)上是减函数，在区间(2，＋∞)上是增函数；③f(x)没有最小值．其中正确的有________个(　　)‎ A．1 B．2‎ C．3 D．0‎ ‎【解析】　函数f(x)＝lg(|x－2|＋1)，‎ 函数f(x＋2)＝lg(|x|＋1)是偶函数；‎ 因为y＝lgx y＝lg(x＋1) y＝lg(|x|＋1) y＝lg(|x－2|＋1)，如图，可知f(x)在(－∞，2)上是减函数，在(2，＋∞)上是增函数；由图象可知函数存在最小值为0.‎ ‎【答案】　B