【数学】山西省晋中市和诚高中有限公司2020-2021学年高二上学期周练试题（8

【数学】山西省晋中市和诚高中有限公司2020-2021学年高二上学期周练试题（8

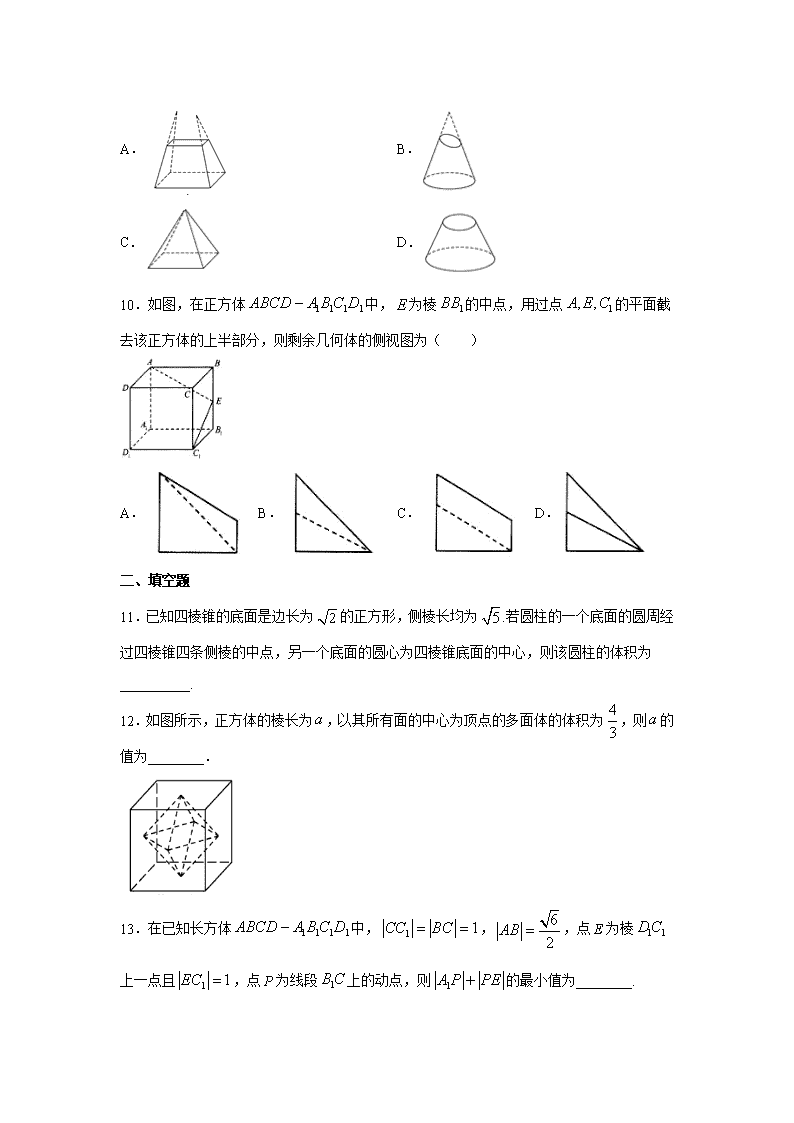
山西省晋中市和诚高中有限公司2020-2021学年 高二上学期周练试题（8.29）‎ 一、单选题 ‎1．下列说法正确的是（ ）‎ A．有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱 B．三棱锥的三个侧面都可以是直角三角形 C．有两个面互相平行，其余各面都是梯形的多面体是棱台 D．以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥 ‎2．某三棱锥的三视图如图所示，该三棱锥的表面积是（ ）‎ A． ‎ B． ‎ B． C． D．‎ ‎3．某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎4．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有 A．14斛 B．22斛 C．36斛 D．66斛 ‎5．如图，正四棱锥底面的四个顶点、、、在球的同一个大圆上，点在球面上，如果，则求的表面积为（ ）‎ A． ‎ B． ‎ B． C． D．‎ ‎6．用斜二测画法画水平放置的的直观图，得到如图所示的等腰直角三角形.已知点是斜边的中点，且，则的边边上的高为（ ）‎ A．1 B．2 C． D．‎ ‎7．已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（　　）‎ A． B． C． D．‎ ‎8．水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图所示，是一个正方体的表面展开图，若图中“2”在正方体的上面，则这个正方体的下面是( )‎ A．0 B．9 ‎ C．快 D．乐 ‎9．下列几何体是台体的是( )‎ A． B．‎ C． D．‎ ‎10．如图，在正方体中，为棱的中点，用过点的平面截去该正方体的上半部分，则剩余几何体的侧视图为（ ）‎ A． B． C． D．‎ 二、填空题 ‎11．已知四棱锥的底面是边长为的正方形，侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为__________.‎ ‎12．如图所示，正方体的棱长为，以其所有面的中心为顶点的多面体的体积为，则的值为________．‎ ‎13．在已知长方体中，，，点E为棱上一点且，点P为线段上的动点，则的最小值为________.‎ 三、解答题 ‎14．如图所示，在四边形ABCD中，，，，，，求四边形ABCD绕AD旋转一周所形成的几何体的表面积及体积.‎ ‎15．如图，有一个水平放置的无盖正方体容器，容器高，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为，若不计容器的厚度，如何求出球的体积？‎ ‎(1)求出球的半径；‎ ‎(2)求球的体积.‎ 参考答案 ‎1．B.‎ ‎2．C 由三视图得出三棱锥的直观图，如下图所示 其中平面，平面，可求得 在中，，可求边上的高为6，所以 则该三棱锥的表面积为 故选：C ‎3．C 由三视图可知几何体为三棱锥，且其直观图为:‎ 几何体底面三角形的面积为，高为1‎ 所以几何体的体积为：.‎ 故答案为：C ‎4．B 试题分析：设圆锥底面半径为r，则，所以，所以米堆的体积为=，故堆放的米约为÷1.62≈22，故选B.‎ ‎5．D 由题意，设半径为，则，，，．‎ ‎∴．‎ 故选：D.‎ ‎6．D ‎【详解】‎ ‎∵直观图是等腰直角三角形，，∴，根据直观图中平行于轴的长度变为原来的一半,‎ ‎∴△的边上的高.故选D.‎ ‎7．C 试题分析：圆锥的表面积是其侧面积与底面积之和,根据题意有侧面积是底面积的2倍.又因为圆锥的侧面展开图是扇形,其圆心角,半径为,且其弧长等于圆锥底面周长,所以,根据扇形面积公式有,代入,得.即圆锥的侧面展开图扇形的圆心角为，故选C.‎ ‎8．B 根据一个正方体的表面展开图以及图中“”在正方体的上面，把该正方体还原，其直观图为：‎ 由直观图可得这个正方体的下面是，故选B．‎ ‎9．D A中几何体四条侧棱的延长线不是相交于一点，所以不是棱台；‎ B中几何体上下底面不平行，所以不是圆台；‎ C中几何体是棱锥，不是棱台；‎ D中几何体侧面的母线延长相交于一点，且上下底面平行，是圆台．故选D．‎ ‎10．C 取中点，连接．平面为截面．如下图：‎ 故选：C ‎11．.‎ 由题意四棱锥的底面是边长为的正方形，侧棱长均为，借助勾股定理，可知四棱锥的高为，.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，圆柱的底面半径为，一个底面的圆心为四棱锥底面的中心，故圆柱的高为，故圆柱的体积为．‎ ‎12．‎ 由图可知以其所有面的中心为顶点的多面体为两个全等的正四棱锥构成，‎ 四棱锥底面四边形面积为正方形面积一半为，‎ 高为正方体棱长一半为，‎ 所以V，解得a=2，‎ ‎13．‎ 如图，将矩形和三角形沿翻折成平面图形，连接交于点P，可知的最小值即为的长 故答案为：‎ ‎14．.‎ 如图，过C作CE垂直于AD，交AD延长线于E，则所求几何 的体积可看成是由梯形ABCE绕AE旋转一周所得的圆台的体积，减去△EDC绕DE旋转一周所得的圆锥的体积．‎ 所以所求几何体的表面积=，体积V＝V圆台－V圆锥＝π×(52＋5×2＋22)×4－π×22×2＝π.‎ ‎15．(1)5；(2).‎ ‎(1)设正方体上底面所在平面截球得小圆，‎ 则圆心为正方体上底面正方形的中心，‎ 设球的半径为，根据题意，球心到上底面的距离等于，‎ 而圆的半径为，由球的截面圆性质，得，‎ 解得；‎ ‎(2)将球的半径代入球的体积公式得.‎