【物理】2020届一轮复习人教版圆周运动及其应用学案

【物理】2020届一轮复习人教版圆周运动及其应用学案

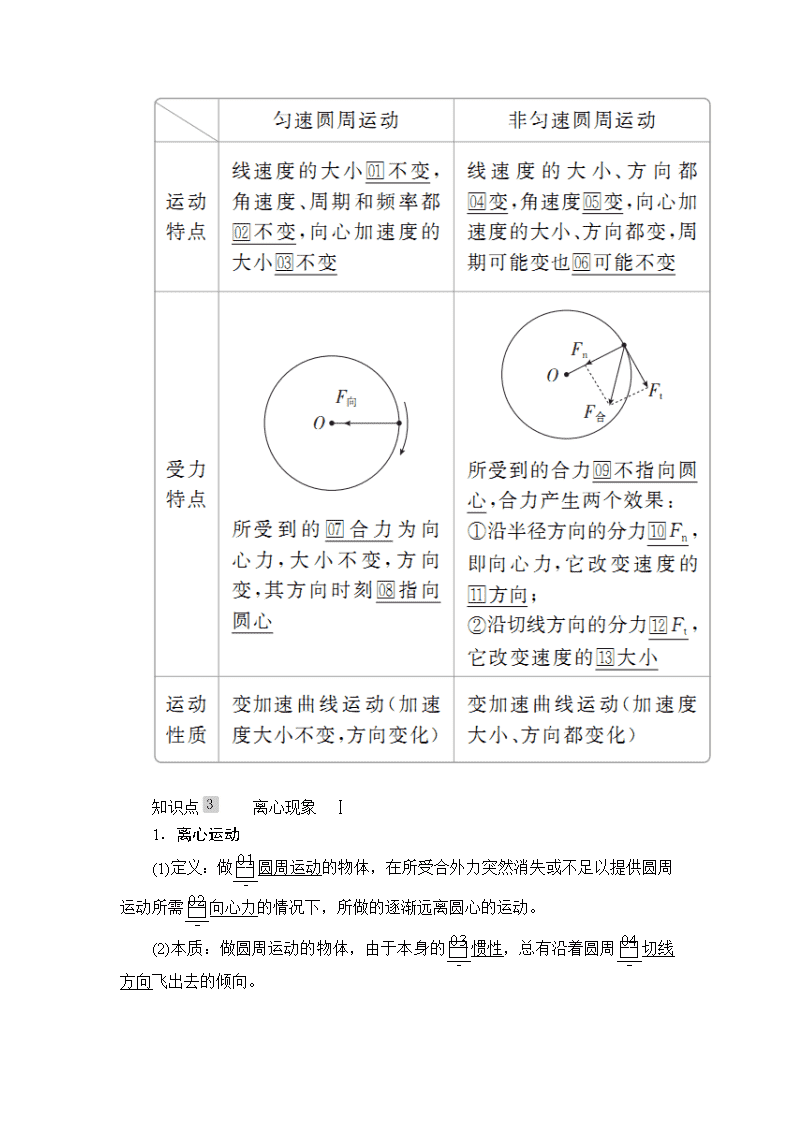
2020 届一轮复习人教版 圆周运动及其应用 学案 主干梳理 对点激活 知识点 匀速圆周运动、角速度、线速度、向心加速度 Ⅰ 匀速圆周运动的向心力 Ⅱ1.匀速圆周运动 (1)定义：线速度大小□01 不变的圆周运动。 (2)性质：加速度大小□02 不变，方向总是指向□03 圆心的变加速曲线运动。 (3)条件：有初速度，受到一个大小不变，方向始终与速度方向□04 垂直且指 向圆心的合外力。 2．描述圆周运动的物理量 描述圆周运动的物理量主要有线速度、角速度、周期、频率、转速、向心加 速度、向心力等，具体如下： 知识点 匀速圆周运动与非匀速圆周运动 Ⅰ 知识点 离心现象 Ⅰ 1．离心运动 (1)定义：做□01 圆周运动的物体，在所受合外力突然消失或不足以提供圆周 运动所需□02 向心力的情况下，所做的逐渐远离圆心的运动。 (2)本质：做圆周运动的物体，由于本身的□03 惯性，总有沿着圆周□04 切线 方向飞出去的倾向。 (3)受力特点：Fn 为提供的向心力。 ①当 Fn＝mω2r 时，物体做□05 匀速圆周运动。 ②当 Fnmω2r 时，物体将逐渐□08 靠近圆心，做近心运动。 一 思维辨析 1．做圆周运动的物体，一定受到向心力的作用，所以分析受力时，必须指 出受到的向心力。( ) 2．匀速圆周运动是匀变速曲线运动，非匀速圆周运动是变加速曲线运动。 ( ) 3．匀速圆周运动的向心加速度与半径成反比。( ) 4．在光滑的水平路面上汽车不可以转弯。( ) 5．摩托车转弯时速度过大就会向外发生滑动，这是摩托车受沿转弯半径向 外的离心力作用的缘故。( ) 6．火车转弯速率小于规定的数值时，内轨受到的压力会增大。( ) 答案 1.× 2.× 3.× 4.√ 5.× 6.√ 二 对点激活 1. (人教版必修 2·P25·T3 改编)如图所示，小物体 A 与水平圆盘保持相对静止， 跟着圆盘一起做匀速圆周运动，则 A 受力情况是( ) A．重力、支持力 B．重力、向心力 C．重力、支持力、指向圆心的摩擦力 D．重力、支持力、向心力、摩擦力 答案 C 解析 A 受三个力作用，重力和支持力平衡，指向圆心的摩擦力充当向心力， 故 C 正确。 2．(人教版必修 2·P22·T1)(多选)甲、乙两物体都在做匀速圆周运动，下列哪 种情况下甲的向心加速度比较大( ) A．它们的线速度相等，乙的半径小 B．它们的周期相等，甲的半径大 C．它们的角速度相等，乙的线速度小 D．它们的线速度相等，在相同时间内甲与圆心的连线扫过的角度比乙的大 答案 BCD 解析 由 a＝v2 r 知当 v 相同的情况下，r 甲>r 乙时，a 甲r 乙时， a 甲>a 乙，故 B 正确；由 a＝ωv 知当ω相同情况下，v 甲>v 乙时，a 甲>a 乙，故 C 正确；由 a＝ωv 知当 v 相同情况下，ω甲>ω乙时，a 甲>a 乙，故 D 正确。 3．(人教版必修 2·P26·T5)一辆汽车在水平公路上转弯，沿曲线由 M 向 N 行 驶，速度逐渐减小。如图 A、B、C、D 分别画出了汽车转弯时所受合力 F 的四 种方向，你认为正确的是( ) 答案 C 解析 汽车沿曲线转弯，所以受到垂直速度方向指向轨迹凹侧的向心力 Fn， 汽车的速度逐渐减小，所以还受到与速度方向相反沿轨迹切线方向的切向力 Ft， 这两个力的合力方向如图 C 所示。 4．下列关于离心现象的说法正确的是( ) A．当物体所受的离心力大于向心力时产生离心现象 B．做匀速圆周运动的物体，当它所受的一切力都突然消失后，物体将做背 离圆心的圆周运动 C．做匀速圆周运动的物体，当它所受的一切力都突然消失后，物体将沿切 线做直线运动 D．做匀速圆周运动的物体，当它所受的一切力都突然消失后，物体将做曲 线运动 答案 C 解析 物体只要受到力，必有施力物体，但“离心力”是没有施力物体的， 故所谓的离心力是不存在的，只要向心力不足，物体就做离心运动，故 A 错误； 做匀速圆周运动的物体，当所受的一切力突然消失后，物体将沿切线做匀速直线 运动，故 B、D 错误，C 正确。 考点细研 悟法培优 考点 1 圆周运动的运动学分析 1．圆周运动各物理量间的关系 2．对公式 v＝ωr 的理解 当 r 一定时，v 与ω成正比； 当ω一定时，v 与 r 成正比； 当 v 一定时，ω与 r 成反比。 3．对 a＝v2 r ＝ω2r 的理解 当 v 一定时，a 与 r 成反比； 当ω一定时，a 与 r 成正比。 4．常见的三种传动方式及特点 (1)皮带传动：如图甲、乙所示，皮带与两轮之间无相对滑动时，两轮边缘 线速度大小相等，即 vA＝vB。 (2)摩擦(齿轮)传动：如图丙所示，两轮边缘接触，接触点无打滑现象时，两 轮边缘线速度大小相等，即 vA＝vB。 (3)同轴转动：如图丁所示，两轮固定在一起绕同一转轴转动，两轮转动的 角速度大小相等，即ωA＝ωB。 例 1 如图所示的皮带传动装置中，右边两轮连在一起同轴转动。图中三轮 半径的关系为：r1＝2r2，r3＝1.5r1，A、B、C 三点为三个轮边缘上的点，皮带不 打滑，则 A、B、C 三点的线速度之比为________；角速度之比为________；周 期之比为________。 解题探究 (1)A、B 两点位于两轮边缘靠皮带传动，那么 vA 与 vB 有什么关 系？ωA 与ωB 有什么关系？ 提示：vA＝vB，ωA ωB ＝r2 r1 。 (2)B、C 为同轴转动的两点，vB 与 vC、ωB 与ωC 的关系是什么？ 提示：ωB＝ωC，vB vC ＝r2 r3 。 尝试解答 1∶1∶3__1∶2∶2__2∶1∶1。 因为 A、B 两轮由不打滑的皮带相连，所以相等时间内 A、B 两点转过的弧 长相等，即 vA＝vB，由 v＝ωr 知ωA ωB ＝r2 r1 ＝1 2 ，又 B、C 是同轴转动，相等时间内 转过的角度相等，即ωB＝ωC，由 v＝ωr 知vB vC ＝r2 r3 ＝ 1 2r1 1.5r1 ＝1 3 。所以 vA∶vB∶vC＝1∶ 1∶3，ωA∶ωB∶ωC＝1∶2∶2，再由 T＝2π ω 可得，TA∶TB∶TC＝1∶1 2 ∶1 2 ＝2∶1∶ 1。 总结升华 解决传动问题的关键 (1)确定属于哪类传动方式，抓住传动装置的特点。 ①同轴转动：固定在一起共轴转动的物体上各点角速度相同；②皮带传动、 齿轮传动和摩擦传动：齿轮传动和不打滑的摩擦(皮带)传动的两轮边缘上各点线 速度大小相等。如例 1，右边两轮为同轴转动；左轮与右边小轮为皮带传动。 (2)结合公式 v＝ωr，v 一定时ω与 r 成反比，ω一定时 v 与 r 成正比，判定各 点 v、ω的比例关系。若判定向心加速度 a 的比例，可巧用 a＝ωv 这一规律。 [变式 1] (2018·福州期末)如图是某共享自行车的传动结构示意图，其中Ⅰ 是半径为 r1 的牙盘(大齿轮)，Ⅱ是半径为 r2 的飞轮(小齿轮)，Ⅲ是半径为 r3 的后 轮。若某人在匀速骑行时每秒踩脚踏板转 n 圈，则下列判断正确的是( ) A．牙盘转动角速度为2π n B．飞轮边缘转动线速度为 2πnr2 C．牙盘边缘向心加速度为2πn2 r2 D．自行车匀速运动的速度为2πnr1r3 r2 答案 D 解析 脚踏板与牙盘同轴转动，二者角速度相等，每秒踩脚踏板 n 圈，因为 转动一圈，相对圆心转的角度为 2π，所以角速度ω1＝2πn，A 错误；牙盘边缘与 飞轮边缘线速度的大小相等，据 v＝rω可知，飞轮边缘上的线速度 v1＝2πnr1，B 错误；牙盘边缘的向心加速度 a＝v21 r1 ＝2πnr12 r1 ＝(2πn)2r1，故 C 错误；飞轮角速 度ω2＝v1 r2 ＝2πnr1 r2 ，自行车后轮角速度与飞轮角速度相等，自行车匀速运动的速度 v＝ω2r3＝2πnr1r3 r2 ，故 D 正确。 考点 2 圆锥摆模型及其临界问题 1．圆锥摆模型的受力特点 受两个力，且两个力的合力沿水平方向，物体在水平面内做匀速圆周运动。 2．运动实例 3．解题方法：①对研究对象进行受力分析，确定向心力来源。②确定圆心 和半径。③应用相关力学规律列方程求解。 4．规律总结 (1)圆锥摆的周期 如图摆长为 L，摆线与竖直方向夹角为θ。 受力分析，由牛顿第二定律得：mgtanθ＝m4π2 T2 r r＝Lsinθ 解得 T＝2π Lcosθ g ＝2π h g 。 (2)结论 ①摆高 h＝Lcosθ，周期 T 越小，圆锥摆转的越快，θ越大。 ②摆线拉力 F＝ mg cosθ ，圆锥摆转的越快，摆线拉力 F 越大。 ③摆球的加速度 a＝gtanθ。 5．圆锥摆的两种变形 变形 1：具有相同锥度角(长度不同)的圆锥摆，如图甲所示。 由 a＝gtanθ知 A、B 的向心加速度大小相等。由 a＝ω2r 知ωA<ωB，由 a＝v2 r 知 vA>vB。 变形 2：具有相同摆高、不同摆长和摆角的圆锥摆，如图乙所示。 由 T＝2π h g 知摆高 h 相同，则 TA＝TB，ωA＝ωB，由 v＝ωr 知 vA>vB，由 a ＝ω2r 知 aA>aB。 例 2 如图所示，用一根长为 l＝1 m 的细线，一端系一质量为 m＝1 kg 的小 球(可视为质点)，另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝ 37°(sin37°＝0.6，cos37°＝0.8，g 取 10 m/s2，结果可用根式表示)，问： (1)若要小球离开锥面，则小球的角速度ω0 至少为多大？ (2)若细线与竖直方向的夹角α＝60°，则小球的角速度ω′为多大？ 解题探究 (1)小球离开锥面的临界条件是什么？ 提示：锥面对小球支持力为零，且细线与竖直方向的夹角为θ。 (2)细线与竖直方向夹角为 60°时，小球受几个力？ 提示：2 个，重力、细线的拉力。 尝试解答 (1)5 2 2 rad/s (2)2 5 rad/s (1)当小球刚要离开锥面时，锥面给小球的支持力为零，受力分析如图 1。 由牛顿第二定律得 mgtanθ＝mω20lsinθ ω0＝ g lcosθ ＝5 2 2 rad/s。 (2)当细线与竖直方向夹角α＝60°时，小球已飞离斜面，受力分析如图 2。 由牛顿第二定律得 mgtanα＝mω′2r r＝lsinα 联立得ω′＝ g lcosα ＝2 5 rad/s。 总结升华 解决圆锥摆临界问题的技巧 圆锥摆的临界问题，主要就是与弹力有关的临界问题。 (1)绳上拉力的临界条件是：①绳恰好拉直且没有弹力。②绳上的拉力恰好 达最大值。 (2)接触或脱离的临界条件是物体与物体间的弹力恰好为零。 (3)对于火车转弯、半圆形碗内的水平圆周运动有两类临界情况：①摩擦力 的方向发生改变；②发生相对滑动。 [变式 2－1] (2018·通州模拟)如图所示，一个内壁光滑的圆锥筒，其轴线垂 直于水平面，圆锥筒固定不动。有一个质量为 m 的小球 A 紧贴着筒内壁在水平 面内做匀速圆周运动，筒口半径和筒高分别为 R 和 H，小球 A 所在的高度为筒 高的一半。已知重力加速度为 g，则( ) A．小球 A 做匀速圆周运动的角速度ω＝ 2gH R B．小球 A 受到重力、支持力和向心力三个力作用 C．小球 A 受到的合力大小为mgR H D．小球 A 受到的合力方向垂直于筒壁斜向上 答案 A 解析 小球受重力、支持力两个力作用，合力方向沿水平方向指向轴线，故 B、D 错误；受力分析如图所示，由牛顿第二定律得 mg tanθ ＝mω2R 2 ，得ω＝ 2g Rtanθ ＝ 2g R ·H R ＝ 2gH R ，故 A 正确；合力大小为 mg tanθ ＝mgH R ，故 C 错误。 [变式 2－2] (多选)如图所示，物体 P 用两根长度相等、不可伸长的细线系 于竖直杆上，它们随杆转动，若转动角速度为ω，则( ) A．ω只有超过某一值时，绳子 AP 才有拉力 B．绳子 BP 的拉力随ω的增大而增大 C．绳子 BP 的张力一定大于绳子 AP 的张力 D．当ω增大到一定程度时，绳子 AP 的张力大于绳子 BP 的张力 答案 ABC 解析 ω较小时，绳子 AP 处于松弛状态，只有ω超过某一值，才产生拉力， A 正确；当 AP、BP 都产生张力之后，受力如图， FBPsinα＝mg＋FAPsinα① FBPcosα＋FAPcosα＝mω2r② 由①②可知 FBP>FAP，随ω的增大 FBP、FAP 都变大，B、C 正确，D 错误。 考点 3 水平转盘上运动物体的临界问题 水平转盘上运动物体的临界问题，主要涉及到与摩擦力和弹力有关的临界极 值问题。 1．如果只有摩擦力提供向心力，物体间恰好不发生相对滑动的临界条件是 物体间恰好达到最大静摩擦力，则最大静摩擦力 Fm＝mv2 r ，方向指向圆心。 2．如果除摩擦力以外还有其他力，如绳两端连接物体随水平面转动，其临 界情况要根据题设条件进行判断，如判断某个力是否存在以及这个力存在时的方 向(特别是一些接触力，如静摩擦力、绳的拉力等)。 3．运动实例 例 3 游乐场中有一种娱乐设施叫“魔盘”，人坐在转动的大圆盘上，当大 圆盘转速增加时，人就会自动滑向盘边缘。如图所示，有 a、b、c 三人坐在圆盘 上，a 的质量最大，b、c 的质量相差不多，但 c 离圆盘中心最远，a、b 离圆盘 中心的距离相等。若三人与盘面间的动摩擦因数均相等，且假定最大静摩擦力等 于滑动摩擦力，则下列说法正确的是( ) A．当圆盘转速增加时，三人同时开始滑动 B．当圆盘转速增加时，b 首先开始滑动 C．当圆盘转速增加时，a 和 c 首先开始滑动 D．当圆盘转速增加时，c 首先开始滑动 解题探究 (1)人和水平圆盘何时发生相对滑动？ 提示：他们之间的摩擦力达最大值时。 (2)如何分析谁先滑动？ 提示：谁的临界角速度小谁先滑动。 尝试解答 选 D。 设圆盘的角速度为ω，则人所受的向心力 F＝mω2R，且未滑动前圆盘上的人 做共轴运动，角速度相同。圆盘上的人受到的最大静摩擦力为 Ff＝μmg。由题意 得，当 mω2R>μmg，即ω2R>μg 时，圆盘上的人开始滑动，c 离圆盘中心最远，当 圆盘转速增加时，c 先开始滑动，之后 a、b 再同时开始滑动，D 正确。 总结升华 解决临界问题的注意事项 (1)先确定研究对象受力情况，看哪些力充当向心力，哪些力可能突变引起 临界问题。 (2)注意分析物体所受静摩擦力大小和方向随圆盘转速的变化而发生变化。 (3)关注临界状态，即静摩擦力达到最大值时。例 3 中，随圆盘转动、静摩 擦力提供向心力，随转速的增大，静摩擦力增大，当达到最大静摩擦力时开始滑 动，出现临界情况，此时对应的角速度为临界角速度。 [变式 3] 两个质量分别为 2m 和 m 的小木块 a 和 b(可视为质点)放在水平圆 盘上，a 与转轴 OO′的距离为 L，b 与转轴的距离为 2L，a、b 之间用长为 L 的 强度足够大的轻绳相连，木块与圆盘的最大静摩擦力为木块所受重力的 k 倍，重 力加速度大小为 g。若圆盘从静止开始绕转轴缓慢地加速转动，开始时轻绳刚好 伸直但无张力，用ω表示圆盘转动的角速度，下列说法正确的是( ) A．a 比 b 先达到最大静摩擦力 B．a、b 所受的摩擦力始终相等 C．ω＝ kg 2L 是 b 开始滑动的临界角速度 D．当ω＝ 2kg 3L 时，a 所受摩擦力的大小为5kmg 3 答案 D 解析 木块随圆盘一起转动，当绳子上无拉力时，静摩擦力提供向心力，由 牛顿第二定律得：Ff＝mω2r，Ffmax＝kmg，联立得ωmax＝ kg r ，故随着ω增大，b 先达到临界角速度，b 先达到最大静摩擦力，故 A 错误。在 b 的静摩擦力没有达 到最大前，由 Ff＝mω2r，a、b 质量分别是 2m 和 m，而圆周运动的半径 r 分别为 L 和 2L，所以开始时 a 和 b 受到的摩擦力是相等的；当 b 受到的静摩擦力达到 最大后，即ω> kg 2L ，对于 b 木块有：kmg＋F＝mω2·2L，对于 a 木块有 f－F＝ 2mω2L，联立得 f＝4mω2L－kmg>kmg；可知二者受到的摩擦力不一定相等，故 B 错误。b 刚要滑动时，对 b 木块有 kmg＋F＝mω20·2L，对 a 木块有 k·2mg－F＝ 2mω20L，联立得 kmg＋2kmg＝4mω20L，得ω0＝ 3kg 4L ，故 C 错误。当ω＝ 2kg 3L 时，b 未滑动，a 所受摩擦力大小 f＝4mω2L－kmg＝5kmg 3 ，故 D 正确。 考点 4 竖直面内的圆周运动——“绳”模型和“杆”模型 1.在竖直平面 内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类：一是无支 撑(如球与绳连接、沿内轨道运动的过山车等)，称为“绳(环)约束模型”，二是 有支撑(如球与杆连接、在弯管内的运动等)，称为“杆(管)约束模型”。 2．绳、杆模型涉及的临界问题 例 4 (2018·山西吕梁模拟)(多选)如图所示，小球在竖直放置的光滑圆形管 道内做圆周运动，内侧壁半径为 R，小球半径为 r，则下列说法正确的是( ) A．小球通过最高点时的最小速度 vmin＝ gR＋r B．小球通过最高点时的最小速度 vmin＝0 C．小球在水平线 ab 以下的管道中运动时，内侧管壁对小球一定无作用力 D．小球在水平线 ab 以上的管道中运动时，外侧管壁对小球一定有作用力 解题探究 (1)该光滑圆形管道属于绳模型还是杆模型？ 提示：杆模型。 (2)杆模型中小球通过最高点的临界速度是多大？ 提示：v＝0。 尝试解答 选 BC。 在最高点，由于外管或内管都可以对小球产生弹力作用，当小球的速度等于 0 时，内管对小球产生弹力，大小为 mg，故最小速度为 0，故 A 错误，B 正确； 小球在水平线 ab 以下管道运动时，由于沿半径方向的合力提供小球做圆周运动 的向心力，所以外侧管壁对小球一定有作用力，而内侧管壁对小球一定无作用力， 故 C 正确；小球在水平线 ab 以上管道运动时，由于沿半径方向的合力提供小球 做圆周运动的向心力，可能外侧管壁对小球有作用力，也可能外侧管壁对小球没 有作用力，故 D 错误。 总结升华 竖直面内圆周运动问题的解题技巧 (1)定模型：首先判断是轻绳模型还是轻杆模型，两种模型过最高点的临界 条件不同。 (2)确定临界点：抓住绳模型中最高点 v≥ gR，以及杆模型中最高点 v≥0 这两个临界条件。 (3)研究状态：通常情况下竖直平面内的圆周运动只涉及最高点和最低点的 运动情况。 4受力分析：对物体在最高点或最低点时进行受力分析，根据牛顿第二定 律列出方程，F 合＝F 向其中 F 合为沿半径方向的合力。 5过程分析：应用动能定理或机械能守恒定律将初、末两个状态联系起来 列方程。 [变式 4－1] (2018·福州质检)如图所示，长均为 L 的两根轻绳，一端共同 系住质量为 m 的小球，另一端分别固定在等高的 A、B 两点，A、B 两点间的距 离也为 L。重力加速度大小为 g。现使小球在竖直平面内以 AB 为轴做圆周运动， 若小球在最高点速率为 v 时，两根轻绳的拉力恰好均为零，则小球在最高点速率 为 2v 时，每根轻绳的拉力大小为( ) A. 3mg B.4 3 3mg C．3mg D．2 3mg 答案 A 解析 当小球到达最高点速率为 v 时，两根轻绳中张力恰好均为零，有 mg ＝mv2 r ；当小球到达最高点速率为 2v 时，设每根轻绳中张力大小为 F，应有 2Fcos30°＋mg＝m2v2 r ，解得 F＝ 3mg，A 正确。 [变式 4－2] 一轻杆一端固定质量为 m 的小球，以另一端 O 为圆心，使小 球在竖直面内做半径为 R 的圆周运动，如图所示，则下列说法正确的是( ) A．小球过最高点时，杆所受到的弹力可以等于零 B．小球过最高点的最小速度是 gR C．小球过最高点时，杆对球的作用力一定随速度增大而增大 D．小球过最高点时，杆对球的作用力一定随速度增大而减小 答案 A 解析 轻杆可对小球产生向上的支持力，小球经过最高点的速度可以为零， 当小球过最高点的速度 v＝ gR时，杆所受的弹力等于零，A 正确，B 错误。若 v< gR，则杆在最高点对小球的弹力竖直向上，mg－F＝mv2 R ，随 v 增大，F 减小； 若 v> gR，则杆在最高点对小球的弹力竖直向下，mg＋F＝mv2 R ，随 v 增大，F 增大，故 C、D 均错误。 考点 5 斜面上圆周运动的临界问题 在斜面上做圆周运动的物体，根据受力情况的不同，可分为以下三类。 1．物体在静摩擦力作用下做圆周运动。 2．物体在绳的拉力作用下做圆周运动。 3．物体在杆的作用下做圆周运动。 这类问题的特点是重力的分力和其他力的合力提供向心力，运动和受力情况 比较复杂。 例 5 (2014·安徽高考) 如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定 对称轴以恒定角速度ω转动，盘面上离转轴距离 2.5 m 处有一小物体与圆盘始终 保持相对静止。物体与盘面间的动摩擦因数为 3 2 (设最大静摩擦力等于滑动摩擦 力)，盘面与水平面的夹角为 30°，g 取 10 m/s2。则ω的最大值是( ) A. 5 rad/s B. 3 rad/s C．1.0 rad/s D．0.5 rad/s 解题探究 (1)随着ω增大会发生什么？ 提示：小物体在圆盘上滑动。 (2)小物体转到哪个位置最容易发生上述情况？ 提示：最低点。 尝试解答 选 C。 当物体转到圆盘的最低点恰好要滑动时，转盘的角速度最大，其受力如图所 示(其中 O 为对称轴位置)。 由沿斜面的合力提供向心力，有 μmgcos30°－mgsin30°＝mω2R 得ω＝ g 4R ＝1.0 rad/s，C 正确。 总结升华 与竖直面内的圆周运动类似，斜面上的圆周运动也是集中分析物体在最高点 和最低点的受力情况，列牛顿运动定律方程来解题。只是在受力分析时，一般需 要进行立体图到平面图的转化，这是解斜面上圆周运动问题的难点。 [变式 5] 如图所示，在倾角为α＝30°的光滑斜面上，有一根长为 L＝0.8 m 的轻杆，一端固定在 O 点，另一端系一质量为 m＝0.2 kg 的小球，沿斜面做圆周 运动，取 g＝10 m/s2，若要小球能通过最高点 A，则小球在最低点 B 的最小速度 是( ) A．4 m/s B．2 10 m/s C．2 5 m/s D．2 2 m/s 答案 A 解析 小球受轻杆控制，在 A 点的最小速度为零，由动能定理可得： mg·2Lsinα＝1 2mv2B－0，可得 vB＝4 m/s，A 正确。 答卷现场 2 水平面内的圆周运动 (16 分)如图所示，半径为 R 的半球形陶罐，固定在可以绕竖直轴旋转的水 平转台上，转台转轴与过陶罐球心 O 的对称轴 OO′重合。转台以一定角速度ω 匀速转动，一质量为 m 的小物块落入陶罐内，经过一段时间后，小物块随陶罐 一起转动且相对罐壁静止，它和 O 点的连线与 OO′之间的夹角θ为 60°，重力加 速度大小为 g。 (1)若ω＝ω0，小物块受到的摩擦力恰好为零，求ω0； (2)ω＝(1±k)ω0，且 0mQ， LPmQ，所以 P 球所受绳的拉力大于 Q 球所受绳的拉力， 故 C 项正确；向心加速度 a＝v2 L ＝2g，所以在轨迹的最低点，P、Q 两球的向心 加速度相同，故 D 项错误。 3．(2017·江苏高考) 如图所示，一小物块被夹子夹紧，夹子通过轻绳悬挂在 小环上，小环套在水平光滑细杆上。物块质量为 M，到小环的距离为 L，其两侧 面与夹子间的最大静摩擦力均为 F。小环和物块以速度 v 向右匀速运动，小环碰 到杆上的钉子 P 后立刻停止，物块向上摆动。整个过程中，物块在夹子中没有 滑动。小环和夹子的质量均不计，重力加速度为 g。下列说法正确的是( ) A．物块向右匀速运动时，绳中的张力等于 2F B．小环碰到钉子 P 时，绳中的张力大于 2F C．物块上升的最大高度为2v2 g D．速度 v 不能超过 2F－MgL M 答案 D 解析 物块受到的摩擦力小于等于最大静摩擦力，即 Mg≤2F。物块向右匀 速运动时，物块处于平衡状态，绳子中的张力 T＝Mg≤2F，A 错误；小环碰到 钉子时，物块做圆周运动，根据牛顿第二定律和向心力公式有：T－Mg＝Mv2 L ，T ＝Mg＋Mv2 L ，所以绳子中的张力与 2F 大小关系不确定，B 错误；物块运动到达 最高点，根据动能定理有－Mgh＝0－1 2Mv2，则最大高度 h＝v2 2g ，C 错误；环碰 到钉子后，物块做圆周运动，在最低点，物块与夹子 间的静摩擦力达到最大值时速度最大，由牛顿第二定律知：2F－Mg＝Mv2 L ， 故最大速度 v＝ 2F－MgL M ，D 正确。 4. (2018·广东佛山质检一)图示为公路自行车赛中运动员在水平路面上急转 弯的情景，运动员在通过弯道时如果控制不当会发生侧滑而摔离正常比赛路线， 将运动员与自行车看做一个整体，下列论述正确的是( ) A．运动员转弯所需向心力由地面对车轮的支持力与重力的合力提供 B．运动员转弯所需向心力由地面对车轮的摩擦力提供 C．发生侧滑是因为运动员受到的合外力方向背离圆心 D．发生侧滑是因为运动员受到的合外力大于所需的向心力 答案 B 解析 运动员转弯所需的向心力由地面对车轮的摩擦力提供，则 A 错误，B 正确。发生侧滑而做离心运动的原因是自行车所受的摩擦力小于所需要的向心 力，故 C、D 错误。 5．(2018·甘肃兰化一中模拟) 如图所示，“旋转秋千”中座椅(可视为质点) 通过轻质缆绳悬挂在旋转圆盘上。当旋转圆盘以角速度ω匀速转动时，不计空气 阻力，缆绳延长线与竖直中心轴相交于 O 点，夹角为θ，O 点到座椅的竖直高度 为 h，则当ω增大时( ) A．h 不变 B．θ减小 C．ω2h 不变 D．ω2h 增大 答案 C 解析 对座椅受力分析如图所示，根据牛顿第二定律可得 mgtanθ＝ mω2htanθ，解得：g＝ω2h，则当ω增大时，h 减小，θ变大，ω2h 不变，故选 C。