八年级下数学课件：16-3 二次根式的加减 （共33张PPT）_人教新课标

八年级下数学课件：16-3 二次根式的加减 （共33张PPT）_人教新课标

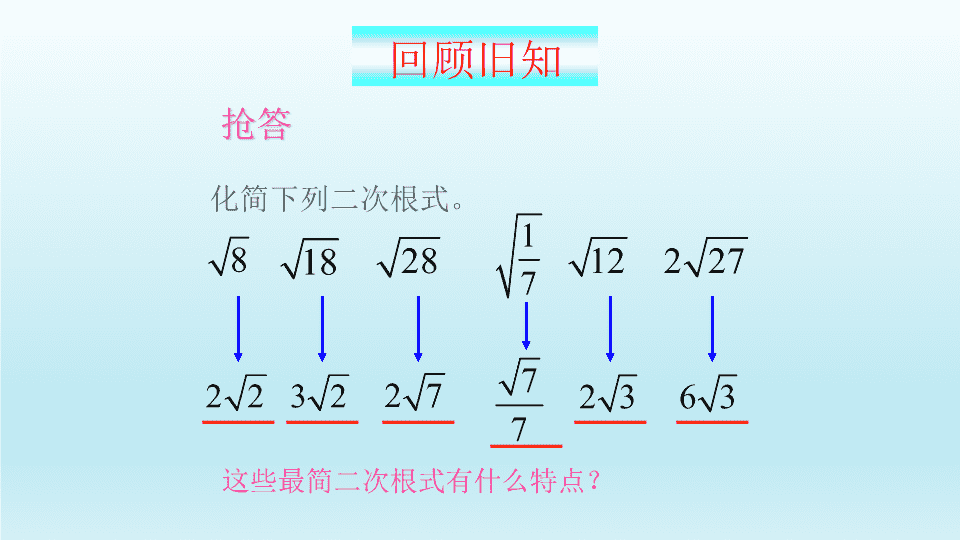
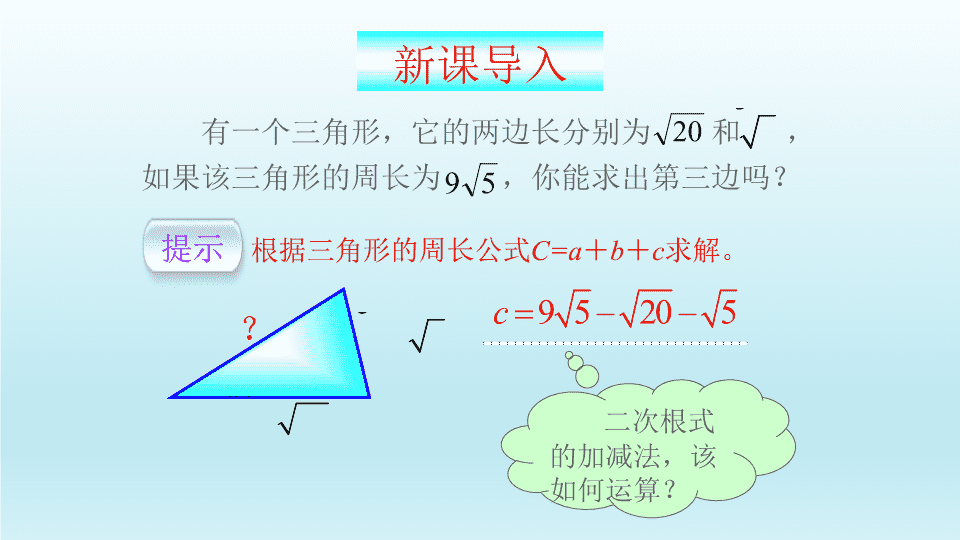
化简下列二次根式。 8 18 28 1 7 12 2 27 2 2 3 2 2 7 7 7 2 3 6 3 这些最简二次根式有什么特点？ 回顾旧知 有一个三角形，它的两边长分别为 和 ， 如果该三角形的周长为 ，你能求出第三边吗？ 20 5 59 9 5 20 5c    根据三角形的周长公式C=a＋b＋c求解。提示 20a  5b ？ 二次根式 的加减法，该 如何运算？ 新课导入 【知识与能力】 Ø了解最简二次根式的概念并灵活运用它们 对二次根式进行加减。 　　 【过程与方法】 Ø通过分析前面的计算和化简结果，抓住它 们的共同特点，给出最简二次根式的概念。 Ø利用最简二次根式的概念，来对相同的二 次根式进行合并，达到对二次根式进行计算 和化简的目的。 教学目标 【情感态度与价值观】 Ø利用规定准确计算和化简的严谨的科学 精神。 Ø经过探索二次根式的重要结论，发展学 生观察、分析、发现问题的能力。 Ø二次根式化简为最简二次根式以及二次 根式的判定。 Ø二次根式的加减、乘除、乘方等运算规 律。 Ø由整式运算知识迁移到含二次根式的运 算。 教学重难点 （化成最简二次根式） （分配律） 二次根式 的加减类似于 什么运算？ 9 5 2 5 5   (9 2 1) 5   6 5 9 5 20 5c    我们可以这样来计算 20a  5b  ？ 计算 2 2 33 2a a a （4） 2 3x x（1） 2 2 22 3 5x x x （2） 3 2 3x x y （ ） 以上，是我们以前所学的整式加减—— 同类项合并。同类项合并就是字母不变，系 数相加减。 5x 24x 3 3x y  2 3a a  回顾 9 2x x x   (9 2 1)x   6x 9 5 2 5 5   (9 2 1) 5   6 5 对比 二次根式的加减 整式的加减 在有理数 范围内成立的 运算律，在实 数范围内仍然 成立。 加法交换律：a+b=b+a 乘法交换律：a×b=b×a 加法结合律：a+b+c=(a+b)+c=a+(b+c) 乘法结合律：(a×b)×c=a×(b×c) 左分配律：c·(a+b)=(c·a)+(c·b) 右分配律：(a+b)·c=(a·c)+(b·c) 部分运算律 现有一块长7.5dm、宽5dm的木板，能否 在这块木板上截出两个面积分别是8dm2和 18dm2的正方形木板？ 实际问题 这两块正方形木板的边长分别为分析 18。8、 5 dm 7.5 dm 8 18 18 8 8 5 18 5  ， ∴木板够宽。 那么木板够长吗？ 8 18（ ） 5 dm 7.5 dm 8 18 18 8 分析 这两块正方形边长的和为 < 7.5 ？ 8 18 2 2 3 2  2 3 2 （ ） 5 2 （化成最简二次根式） （分配律） 5 2 7.5 ∴木板够长，可以截出这两个正方形木板。 同类二次根式 2 2 3 2 2 7 7 7 2 3 6 3 几个二次根式化成最简二次根式后，如 果被开方数相同，这几个二次根式就叫做同 类二次根式。 判断一组式子是否为同类二次根式，只 需看化为最简二次根式后的被开方数是否相 同，与最简二次根式前面的因式及符号无关。 注意 1.说出 的三个同类二次根式。 2.下列各式中哪些是同类二次根式？ 33 2 2 68 3 23 27 1 50 1752 , b ab,ab,,,,, 2 2x 22a x 5 3 2 10 3 9 4 2 3 b ab 3 2ab√√ √ √√ √ √ 22y x 418xy 8 18 2 2 3 2  2 3 2 （ ） 5 2 9 5 2 5 5   (9 2 1) 5   6 5 9 5 20 5  归纳 二次根式加减时，可以先将二 次根式化成最简二次根式，再将被 开方数相同的二次根式进行合并。 知识要点 下列算法正确吗？ 3 2 5  a b a b  a b a b   ( )a a b a a b a   1 13 2 0 3 2 a a a a    √ × × × × 例题 计算 4 5 2 5 5   4 2 1 5   3 5 （1） （1）如果几个二次根式的被开方数相同， 那么可以直接根据分配律进行加减运算。 注意 （2）如果所给的二次根式不是最简二 次根式，应该先化简，再进行加减运算。 注意 （2） 2 3 2 5 3 5    3 3 5  2 3 3 2 5 5    交换律在 二次根式运算 中仍然成立。    12 20 3 5   二次根式加减运算的步骤 （3）合并同类二次根式。 （1）将每个二次根式化为最简二次根式。 （2）找出其中的同类二次根式。 一化 二找 三合并 如图所示的Rt△ABC中，∠B=90°，点P从点B 开始沿BA边以1cm/s的速度向点A移动。同时，点Q 也从点B开始沿BC边以2cm/s的速度向点C移动。问： 几秒后△PBQ的面积为35cm2？PQ的距离是多少厘米？ （结果用最简二次根式） 例题 解答 A CB Q P 解：设x秒后△PBQ的面积为35cm2， 则有PB=x，BQ=2x。 A CB Q P 1cm/s 2cm/s 1 2 35 2 x x 由题意得， 2 35x  35x  2 2 2 2 24 5 5 35 5 7PQ PB BQ x x x        答： 秒后△PBQ的面积为35cm2， PQ的距离为 cm。 35 5 7 例题 计算  8 3 6  4 3 3 2  8 6 3 6    8 6 3 6    (4 2 3 6) 2 2  4 2 2 2 3 6 2 2 32 3 2       （1）加减与乘除的混合运算，先乘除， 后加减，使难点分散。 （2）在运算中，对于各根式不一定要先 化简，而是先乘除，进行约分，达到化简的 目的，但最后结果一定要化简。 注意 例题 计算   5 3 5 3   2 3 2 5     2 2 5 3  2 2 3 2 5 2 15    13 2 2   2 2 2 15   2 5 3  注意 观察算式，找出特征，利用多项式乘法 法则和乘法公式求解。 2 2( )( )a b a b a b    平方差公式 回顾 如果分母是二次根式，采用分子、分母 同乘以分母的的方法进行化简。 怎样化简？ （依据分式的基本性质） 如果分母是含二 次根式的两个因式的 和或差，怎样化简？ 3 2 2 3 2 2   、 a b a b   1 3 2 2 、 a b a b   分母乘以什 么样的式子，就 能将分母的根号 去掉？ 2 2( ))(a ba b a b   平方差公式 如果分母是含二次根式的两个因式的和 或差，采用分子、分母同乘以分母的有理化 因式的方法进行化简。 1 3 2 2   a b a b    1 3 2 2 3 2 2 3 2 2      （ ） （ ） （ ） a a b a b a b b        （ ） （ （） （ ） ） 例题 化简 有理化因式 有理化因式 2 2 3 2 2 3 2 2   （ ） 3 2 2 9 8   3 2 2  2 2 2 a b a b    （ ） （ ）（ ） 2a ab b a b    3 2 3 3 2 3 1a  1a  与 与 a b 与 a b 1a  1a 与 1 3 6 3 6与 √ × × × √ 例题 计算 有关二次根式的除法，可先写成分式的 形式，然后通过分母有理化进行运算。 注意  2 3 2  2 3 2   2 3 2 3 2 3 2       （ ） （（ ） ） 2 2 2 3 2 2 3 2    （ ） （ ） 3 2 2 9 2    3 2 2 7   1.同类二次根式： 几个二次根式化成最简二次根式后，如 果被开方数相同，这几个二次根式就叫做同 类二次根式。 课堂小结 2.二次根式加减运算的步骤： （3）合并同类二次根式。 （1）将每个二次根式化为最简二次根式。 （2）找出其中的同类二次根式。 一化 二找 三合并 3.有理化因式： （1）单独一项 的有理化因式就是它本身 。 （2）出现和、差形式的：如 的有理化因式为 a a a b a b 。 谢 谢