- 2021-05-26 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版七年级上册-第01讲- 丰富的图形世界 (提高)-教案
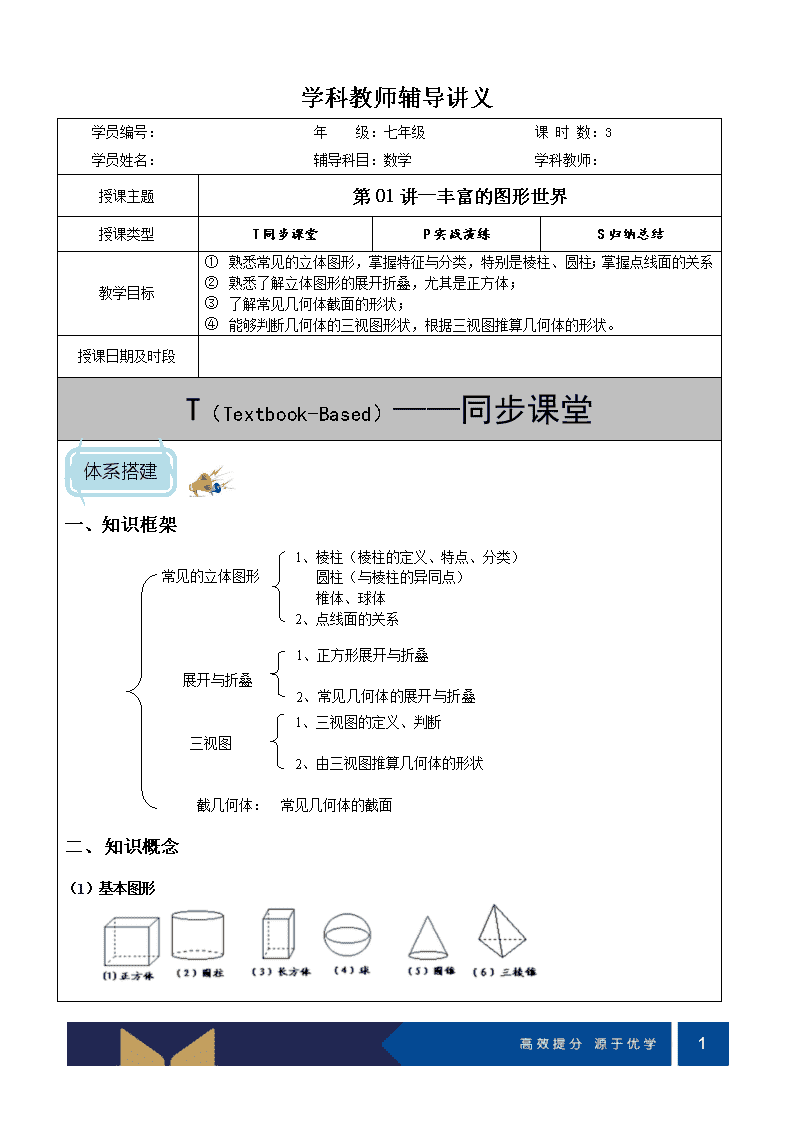
1 学科教师辅导讲义 学员编号: 年 级:七年级 课 时 数:3 学员姓名: 辅导科目:数学 学科教师: 授课主题 第 01 讲—丰富的图形世界 授课类型 T 同步课堂 P 实战演练 S 归纳总结 教学目标 1 熟悉常见的立体图形,掌握特征与分类,特别是棱柱、圆柱;掌握点线面的关系 2 熟悉了解立体图形的展开折叠,尤其是正方体; 3 了解常见几何体截面的形状; 4 能够判断几何体的三视图形状,根据三视图推算几何体的形状。 授课日期及时段 T(Textbook-Based)——同步课堂 体系搭建 一、知识框架 常见的立体图形 展开与折叠 1、三视图的定义、判断 三视图 2、由三视图推算几何体的形状 截几何体: 常见几何体的截面 二、知识概念 (1)基本图形 1、棱柱(棱柱的定义、特点、分类) 圆柱(与棱柱的异同点) 椎体、球体 2、点线面的关系 1、正方形展开与折叠 2、常见几何体的展开与折叠 叠 2 几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形。 立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就 是立体图形。 (2)棱柱及其有关概念、点线面的关系 棱:在棱柱中,任何相邻两个面的交线,都叫做棱。 侧棱:相邻两个侧面的交线叫做侧棱。 n 棱柱有两个底面,n 个侧面,共(n+2)个面;3n 条棱,n 条侧棱;2n 个顶点。 点是所有图形的基础;线是点的移动轨迹,有长短、粗细之分;面就是由无数条线组成的。 (3)三视图 主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形。 (4)图形的展开和折叠 图形的展开:沿图形的表面的棱将图形展开。图形的折叠:将展开的平面图形折叠 正方体的展开图可以归为四大类:二二二型;三三型;二三一型(或一三二型);一四一型。正方体的表 面展开图不能出现“田”字形与“凹”字形。 典例分析 考点一: 棱柱 例 1、下列图形属于棱柱的有( ) A、2 个 B、3 个 C、4 个 D、5 个 【解析】根据棱柱的概念、结合图形解得即可。第一、二、四个几何体是棱柱,故选:B 例 2、对棱柱而言,下列说法错误的是( ) A、所有侧面都是长方形 B、所有侧棱长都相等 C、上、下底面的形状相同 D、相邻两个侧面的交线叫做侧棱 【解析】A、所有的侧面不一定是长方形,说法错误 B、所有的侧棱长都相等,说法正确; C、上、下底面的形状相同,说法正确 D、相邻两侧面的交线叫侧棱,说法正确。 故选 A 例 3、下列说法中,正确的个数是( ) 3 ①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体; ⑤棱柱的侧面一定是长方形 【解析】①柱体包括圆柱、棱柱;柱体的两个底面一样大;正确 ②圆柱、圆锥的底面都是圆,正确; ③棱柱的底面可以为任意多边形,错误; ④长方体符合柱体的条件,一定是柱体,正确; ⑤棱柱的侧面应是长方形,正确;共有 4 个正确,故选 C. 注意棱柱由上下两个底面以及侧面组成;上下两个底面可以是全等的多边形,侧面是四边形 例 4、如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱 锥.如图是一个四棱柱和一个六棱锥,它们各有 12 条棱.下列棱柱中和九棱锥的棱数相等的是( ) A、五棱柱 B、六棱柱 C、七棱柱 D、八棱柱 【解析】九棱锥侧面有 9 条棱,底面是九边形,也有 9 条棱,共 9+9=18 条棱, A、五棱柱共 15 条棱,故 A 错误 B、六棱柱共 18 条棱,故 B 正确; C、七棱柱共 21 条棱,故 C 错误 D、八棱柱共 24 条棱,故 D 错误; 故选:B 例 5、笔尖在纸上写字说明( );车轮旋转时看起来像个圆面,这说明( );一枚硬币在光 滑的桌面上快速旋转形成一个球,这说明( )。 【解析】点动成线,线动成面,面动成体 考点二:展开与折叠 例 1、如图是一个正方体,则它的表面展开图可以是( ) A、 B、 C、 D、 【解析】根据含有“田”字形和“凹”字形的图形不能折成正方体即可判断如下: 4 A、含有田字形,不能折成正方体,故 A 错误; B、属于二三一型,能折成正方体,故 B 正确; C、凹字形,不能折成正方体,故 C 错误; D、含有田字形,不能折成正方体,故 D 错误。 故选:B 例 2、如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( ) A、的 B、中 C、国 D、梦 【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一 特点作答。 “们”与“中”是相对面,“我”与“梦”是相对面,“的”与“国”是相 对面。故选:D 例 3、下列四个图形中是三棱柱的表面展开图的是( ) A、 B、 C、 D、 【解析】利用棱柱及表面展开图的特点:棱柱表面展开图中,上、下两底面应在侧 面展开图长方形的两侧 A、是三棱柱的平面展开图 B、围成三棱柱时,两个三角形重合为同一底面,而另一底面没有,故不能围成三棱柱,故此选项错误; C、围成三棱柱时,缺少一个底面,故不能围成三棱柱,故此选项错误; D、围成三棱柱时,没有底面,故不能围成三棱柱,故此选项错误. 故选:A 例 4、如图是某些几何体的表面展开图,则这些几何体分别是 图 1: 图 2: 图 3: 【解析】根据常见立体图形的展开图特点,结合展开图进行解 答 图 1:两个圆作为底面,一个长方形作为侧面,组成圆柱; 图 2:一个圆与一个扇形可围成圆锥; 图 3:两个三角形作为底面,三个长方形作为侧面,组成三棱柱。 5 例 5、如图的正方体盒子的外表面上画有 3 条粗黑线,将这个正方体盒子的表面展开(外 表面朝上),展开图可能是( ) A、 B、 C、 D、 【解析】本题主要考查了几何体的展开图,注意正方体的空间图形,从相对面入手。 根据正方体的表面展开图,两条黑线在一列,故 A 错误。且两条相邻成直角,故 B 错误。正视图的斜线方 向相反,故 C 错误。只有 D 选项符合条件,故选 D 考点三: 三视图 例 1、下列四个立体图形中,主视图为圆的是( ) A、 B、 C、 D、 菁优网 【解析】主视图是从物体的正面看得到的图形,分别写出每个选项中的主视图, 即可得到答案。 A、主视图是正方形,故此选项错误;B、主视图是圆,故此选项正确; C、主视图是三角形,故此选项错误;D、主视图是长方形,故此选项错误; 故选:B 例 2、如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有 (填 编号) 权所 【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形。 ①圆锥主视图是三角形,左视图也是三角形;②圆柱的主视图和左视图都是矩形;③球的主视图和左视图 都是圆形;④长方体的主视图是矩形,左视图也是矩形,但长和宽不一定相同。故选:①②③ 例 3、画出下图所示物体的三视图 6 【解析】只要画出主视图:是从正面看到的图形;左视图:从左面看到 的图形;俯视图:从上面看到的图形。如图所示: 例 4、一个物体由多个完全相同的小正方体组成,它的三视图如图所示, 那么组成这个物体的小正方体的个数为( ) A、2 个 B、3 个 C、5 个 D、10 个 【解析】此题主要考查了由三视图判定几何体的形状,从主视图与左视图可以 得出此图形只有一排,从俯视图可以验证这一点,从而确定个数。从主视图与 左视图可以得出此图形只有一排,只能得出一共有 5 个小正方体,从俯视图可以验证这一点,从而确定小 正方体总个数为 5 个。故选 C 例 5、由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数 最少是( ) A、3 B、4 C、5 D、6 【解析】根据三视图的知识,主视图是由 4 个小正方形组成,而左视图是由 4 个小正方形组成,故这个几 何体的底层最少有 3 个小正方体,第 2 层最少有 1 个小正方体。这个几何体的底层最少有 1+1+1=3 个小正 方体,第二层最少有 1 个小正方体,如由上图所示,因此组成这个几何体的小正方体最少有 3+1=4 个,如 由上图所示。故选: 考点四:截几何体 例 1、一个几何体被一个平面所截后,得到一个圆形截面,则原几何体的形状是( ) A、圆柱 B、圆锥 C、球 D、以上都可以 【解析】本题中,用一个平面截圆柱和圆锥,当截面与底面平行时,可以得到圆形截面;球无论怎么截, 所得截面都是圆。故选 D 7 例 2、在下列几何体中,截面不是等腰梯形的是( ) A、圆台 B、圆柱 C、正方体 D、三棱柱 【解析】根据正方体、圆柱、圆台、三棱柱的形状特点判断即可。 A、根据圆台的定义,即以直角梯形垂直于底边的腰所在直线为旋转轴,其余各边旋转而形成的曲面所围成 的几何体叫做圆台.那么它的截面一定是等腰梯形,故选项不符合; B、根据圆柱的定义,即以矩形的一边所在的直线为旋转轴旋转而成,则它的截面一定是矩形,故选项符合; C、正方体的截面可能是三角形、四边形、五边形、六边形,四边形中可能是等腰梯形,故选项不符合; D、三棱柱的截面可能是等腰梯形,故选项不符合。 故选 B 例 3、用一平面去截如图 5 个几何体,能得到长方形截面的几何体的个数是( ) A、4 B、3 C、2 D、1 【解析】根据长方体、圆柱、三棱柱、圆锥、球的形状判断即可,可用排除法。圆锥、球不可能得到长方 形截面,故能得到长方形截面的几何体有:长方体、圆柱、三棱柱一共有 3 个。故选:B P(Practice-Oriented)——实战演练 实战演练 课堂狙击 1、如下图,下列图形属于柱体的是( ) A、 B、 C、 D、 【解析】分别分析各图形的特点,据此作答。 A、有一个是三棱锥,故不符合题意; B、有一个是不规则的多面体,故不符合题意; C、分别是一个圆柱体、两个四棱柱; D、有一个是圆台,故不符合题意。 故选 C 8 2、请写出棱柱与圆柱的共同点_____、_____,以及不同点 _____、_____(至少二个) 【解析】圆柱与棱柱的共同点:圆柱与棱柱都有两个底面且底面形状、大 小完全相同。不同点:(1)圆柱的底面是圆,棱柱的底面是多边形;(2)圆柱的侧面是一个曲面,棱柱的侧 面是由几个平面围成的,且每个平面都是平行四边形。 3、如图绕虚线旋转得到的几何体是( ) A、 B、 C、 D、 【解析】根据旋转及线动成面的知识可得旋转后的图形为:两边为圆锥,中间为圆柱。故选 D 4、下面图形经过折叠不能围成棱柱的是( ) A、 B、 C、 D、 【解析】利用棱柱及表面展开图的特点:棱柱表面展开图中,上、下两底面应在侧面展开图长方形的两侧 A、能围成四棱柱;B、能围成五棱柱; C、能围成三棱柱;D、经过折叠不能围成棱柱。故选 D 5、下列图形中,不可以作为一个正方体的展开图的是( ) A、 B、 C、 D、 【解析】正方体的展开图可以归为四大类:二二二型;三三型;二三一型(或一三二型);一四一型。正 方体的表面展开图不能出现“田”字形与“凹”字形。 A、属于二三一型,可以作为一个正方体的展开图 B、属于一四一型,可以作为一个正方体的展开图 C、不属于任何正确类型,不能作为一个正方体的展开图 D、属于一四一型,可以作为一个正方体的展开图 故选 C 6、如图是正方体的平面展开图,每个面上都标有一个汉字,与“自”字相对的面上的字是 . 9 【解析】由平面图形的折叠及立体图形的表面展开图的特点解题,正方体的平面展开图中,相对面的特点 是之间一定相隔一个正方形,所以与“自”字相对的面上的字是“超”. 故答案为“超”。 7、将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( ) A、 B、 C、 D、 【解析】由平面图形的折叠及立体图形的表面展开图的特点解题.注意带图案的三个面相交于一点。由原 正方体知,带图案的三个面相交于一点,而通过折叠后 A、B 都不符合,且 D 折叠后图案的位置正好相反, 所以能得到的图形是 C。故选 C 8、如图是由一些大小相同的小立方体组成的几何体的主视图和左视图,则组成这个几何体的小立方体的个 数不可能是( ) A、3 B、4 C、5 D、6 【解析】主视图、左视图是分别从物体正面、左面看,所得到的图形。根据 主视图与左视图,第一行的正方体有 1(只有一边有)或 2(左右都有)个, 第二行的正方形可能有 2(左边有)或 3(左右都有)个,故有 1+2=3,1+3=4, 2+2=4,2+3=5,故不可能有 6 个。故选 D 9、超市货架上摆放着某品牌方便面,如图是它们的三视图,则货架上的方便面至少有( ) A、8 B、9 C、10 D、11 【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形。易得第一层有 4 碗, 第二层最少有 3 碗,第三层最少有 2 碗,所以至少共有 9 个碗。故选:B 10、一个正方体物体,被切一刀后,它的切面不可能是 (写出所有的答案) 【解析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形, 10 但不可能得到等腰直角三角形, 正五边形。故答案为:F,G 课后反击 1、下列说法中,正确的有( ) ①圆锥和圆柱的底面都是圆 ②棱锥底面边数与侧棱数相等 ③棱柱的上下底面是形状、大小相同的多边形 ④正方体是四棱柱,四棱柱是正方体 A、1 个 B、2 个 C、3 个 D、4 个 【解析】此题抓住圆柱、圆锥、棱锥棱柱的结构特征进行判断。 ①由圆柱和圆锥的特征可以得知:圆柱、圆锥的底面都是圆形,故①正确; ②棱锥底面边数与侧棱数相等,故②正确; ③棱柱的上下底面是全等的多边形,则棱柱的上下底面是形状、大小相同的多边形,故③正确; ④正方体是四棱柱,但是四棱柱不一定是正方体,故④错误。 综上所述,正确的说法是:①②③,故选 C 2、下面的几何体中,属于棱柱的有( ) A、1 个 B、2 个 C、3 个 D、4 个 【解析】根据有两个面平行,其余各面都是平行四边形,并且每相邻两个平行四边形的公共边都互相平行, 由这些面所围成的几何体叫 做棱柱,可得答案。从左到 右依次是长方体,圆柱,棱 柱,棱锥,圆锥,棱柱。故选 C 3、下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线 有 【解析】根 据几何体的平面展开图的特征可知:(1)是五棱柱的展开图;(2)是圆锥的展开图;(3)是圆柱的展开图; 11 (4)是正方体的展开图;(5)是两个四棱锥的展开图。 4、小军将一个直角三角板(如下左图)绕它的一条直角边所在的直线旋转一周形成一个几何,将这个几何 体的侧面展开得到的大致图形是( ) A、 B、 C、 D、 【解析】三角板绕直角边旋转,得到的立体图形是圆锥,圆锥展开图如答案 D 所示,故选 D 5、下列各图不是正方体表面展开图的是( ) A. B. C. D. 【解析】正方体的展开图可以归为四大类:二二二型;三三型;二三一型(或一三二型);一四一型。正 方体的表面展开图不能出现“田”字形与“凹”字形。A,C,D 是正方体的平面展开图,B 有田字格,不是 正方体的平面展开图。故选:B 6、 如图,为一正方体的侧面展开图,那么“于”字所在的面与“ ”字所在的面 是对面。 【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特 点作答。根据正方体的表面展开图,相对的面之间一定相隔一个正方形,“于” 的对面是“聪”,“明”的对面是“学”,“在”的对面是“习”。故答案为: 聪 7、如图所示,这个几何体的展开图形是( ) A、 B、 C、 D、 【解析】由平面图形的折叠及立体图形的表面展开图的特点解题。同时注意图示中的各种符号的位置关系。 选项 B、C 中折叠后带图案的三个面不能相交于同一个点,与原立方体不符;选项 D 中折叠后三角形和圆的 位置不符,所以正确的是 A。故选:A 12 8、一个由小立方块搭成的几何体,从正面、左面、上面 看到的形状图如图所示,这个几何体是由( )个小立 方块搭成的。 A、4 B、5 C、6 D、7 【解析】从俯视图中可以看出最底层小立方块的个数及形状,从主视图可以看出每一层小立方块的层数和 个数,从左视图可看出每一行小立方块的层数和个数,从而算出总的个数。由俯视图易得最底层小立方块 的个数为 4,由其他视图可知第二层有一个小立方块,那么共有 4+1=5 个小立方块。故答案为:B 9、用一个平面去截一个几何体,若截面是长方形,则该几何体可能是_____、_____、 _____、(写三个) 【解析】用一个平面去截一个几何体,若截面是长方形,则该几何体可能是:圆柱、长方体、直三棱柱 直击中考 1、【2016 深圳】把下列图形折成一个正方体的盒子,折好后与“中”相对的字是( ) A、祝 B、你 C、顺 D、利 【解析】由正方体折叠及展开图的特点解题,正方体的平面展开图中,相对面的特点 是之间一定相隔一个正方形,所以与“中”字相对的面上的字是“顺”。故答案为 C。 2、【2015 深圳】下列主视图正确的是( ) 【解析】主视图是从物体的正面看得到的图形,由图可知,答案 A 是其主视图,故选 A。 3、【2014 深圳】由几个大小不同的正方形组成的几何图形如图,则它的俯视图是( ) 13 A、 B、 C、 D、 【解 析】 俯视图是从物体的上 面看得到的图形,由图可知,答案 A 是其主视图,故选 A。 S(Summary-Embedded)——归纳总结 重点回顾 1、棱柱(棱柱的定义、特点、分类) 2、正方形展开与折叠 3、三视图 名师点拨 1、正方体的展开图可以归为四大类:二二二型;三三型;二三一型(或一三二型);一四一型。正方体的 表面展开图不能出现“田”字形与“凹”字形 2、通过三视图判断几何体形状:俯视图打地基,正视图疯狂盖,左视图拆违章 学霸经验 本节课我学到了 我需要努力的地方是查看更多