北京市2008-2019年中考数学分类汇编圆pdf含解析

北京市2008-2019年中考数学分类汇编圆pdf含解析

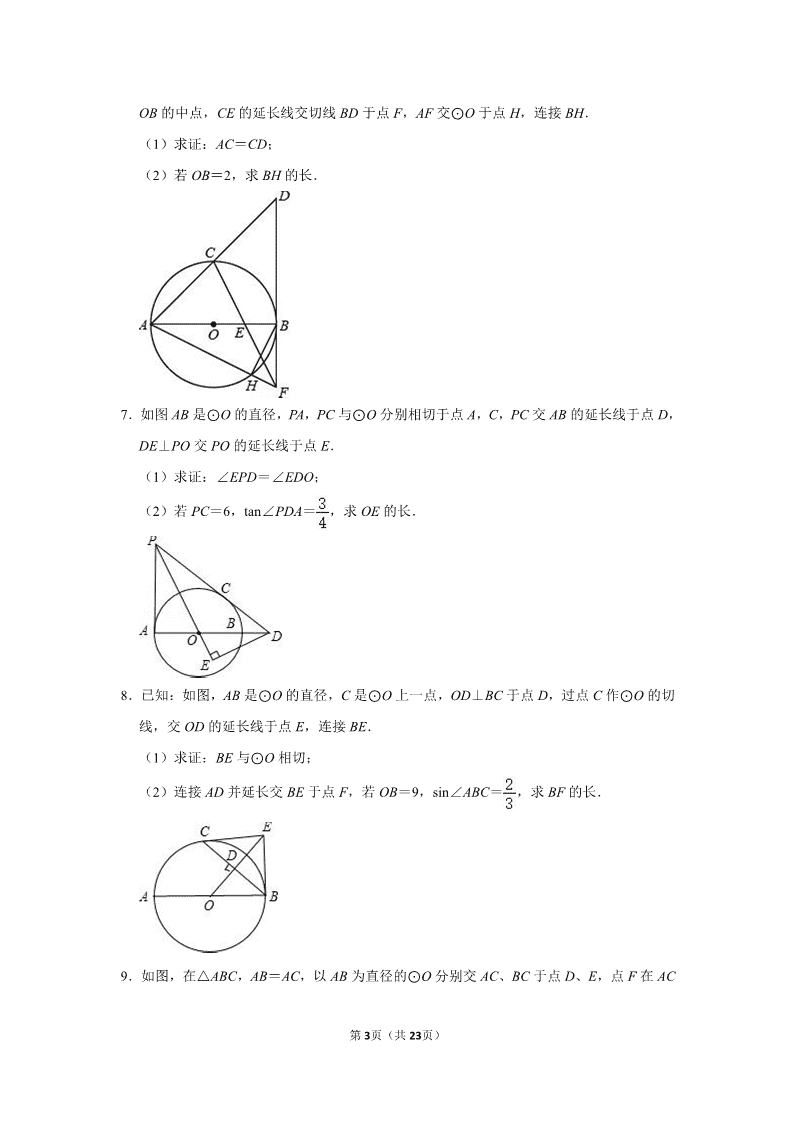
第 1页（共 23页） 2008～2019 北京中考数学分类(圆) 一．解答题（共 12 小题） 1．在平面内，给定不在同一条直线上的点 A，B，C，如图所示，点 O 到点 A，B，C 的距 离均等于 a（a 为常数），到点 O 的距离等于 a 的所有点组成图形 G，∠ABC 的平分线交 图形 G 于点 D，连接 AD，CD． （1）求证：AD＝CD； （2）过点 D 作 DE⊥BA，垂足为 E，作 DF⊥BC，垂足为 F，延长 DF 交图形 G 于点 M， 连接 CM．若 AD＝CM，求直线 DE 与图形 G 的公共点个数． 2．如图，AB 是 ⊙ O 的直径，过 ⊙ O 外一点 P 作 ⊙ O 的两条切线 PC，PD，切点分别为 C， D，连接 OP，CD． （1）求证：OP⊥CD； （2）连接 AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求 OP 的长． 第 2页（共 23页） 3．如图，AB 是 ⊙ O 的一条弦，E 是 AB 的中点，过点 E 作 EC⊥OA 于点 C，过点 B 作 ⊙ O 的切线交 CE 的延长线于点 D． （1）求证：DB＝DE； （2）若 AB＝12，BD＝5，求 ⊙ O 的半径． 4．如图，AB 为 ⊙ O 的直径，F 为弦 AC 的中点，连接 OF 并延长交 于点 D，过点 D 作 ⊙ O 的切线，交 BA 的延长线于点 E． （1）求证：AC∥DE； （2）连接 CD，若 OA＝AE＝a，写出求四边形 ACDE 面积的思路． 5．如图，AB 是 ⊙ O 的直径，过点 B 作 ⊙ O 的切线 BM，弦 CD∥BM，交 AB 于点 F，且 ＝ ，连接 AC，AD，延长 AD 交 BM 于点 E． （1）求证：△ACD 是等边三角形； （2）连接 OE，若 DE＝2，求 OE 的长． 6．如图，AB 是 ⊙ O 的直径，C 是 的中点， ⊙ O 的切线 BD 交 AC 的延长线于点 D，E 是 第 3页（共 23页） OB 的中点，CE 的延长线交切线 BD 于点 F，AF 交 ⊙ O 于点 H，连接 BH． （1）求证：AC＝CD； （2）若 OB＝2，求 BH 的长． 7．如图 AB 是 ⊙ O 的直径，PA，PC 与 ⊙ O 分别相切于点 A，C，PC 交 AB 的延长线于点 D， DE⊥PO 交 PO 的延长线于点 E． （1）求证：∠EPD＝∠EDO； （2）若 PC＝6，tan∠PDA＝ ，求 OE 的长． 8．已知：如图，AB 是 ⊙ O 的直径，C 是 ⊙ O 上一点，OD⊥BC 于点 D，过点 C 作 ⊙ O 的切 线，交 OD 的延长线于点 E，连接 BE． （1）求证：BE 与 ⊙ O 相切； （2）连接 AD 并延长交 BE 于点 F，若 OB＝9，sin∠ABC＝ ，求 BF 的长． 9．如图，在△ABC，AB＝AC，以 AB 为直径的 ⊙ O 分别交 AC、BC 于点 D、E，点 F 在 AC 第 4页（共 23页） 的延长线上，且∠CBF＝ ∠CAB． （1）求证：直线 BF 是 ⊙ O 的切线； （2）若 AB＝5，sin∠CBF＝ ，求 BC 和 BF 的长． 10．已知：如图，在△ABC 中，D 是 AB 边上一点，圆 O 过 D、B、C 三点，∠DOC＝2∠ ACD＝90°． （1）求证：直线 AC 是圆 O 的切线； （2）如果∠ACB＝75°，圆 O 的半径为 2，求 BD 的长． 11．已知：如图，在△ABC 中，AB＝AC，AE 是角平分线，BM 平分∠ABC 交 AE 于点 M， 经过 B，M 两点的 ⊙ O 交 BC 于点 G，交 AB 于点 F，FB 恰为 ⊙ O 的直径． （1）求证：AE 与 ⊙ O 相切； （2）当 BC＝4，cosC＝ 时，求 ⊙ O 的半径． 12．已知：如图，在 Rt△ABC 中，∠C＝90°，点 O 在 AB 上，以 O 为圆心，OA 长为半径 的圆与 AC，AB 分别交于点 D，E，且∠CBD＝∠A． （1）判断直线 BD 与 ⊙ O 的位置关系，并证明你的结论； （2）若 AD：AO＝8：5，BC＝2，求 BD 的长． 第 5页（共 23页） 第 6页（共 23页） 2008～2019 北京中考数学分类(圆) 参考答案与试题解析 一．解答题（共 12 小题） 1．在平面内，给定不在同一条直线上的点 A，B，C，如图所示，点 O 到点 A，B，C 的距 离均等于 a（a 为常数），到点 O 的距离等于 a 的所有点组成图形 G，∠ABC 的平分线交 图形 G 于点 D，连接 AD，CD． （1）求证：AD＝CD； （2）过点 D 作 DE⊥BA，垂足为 E，作 DF⊥BC，垂足为 F，延长 DF 交图形 G 于点 M， 连接 CM．若 AD＝CM，求直线 DE 与图形 G 的公共点个数． 【解答】（1）证明：∵到点 O 的距离等于 a 的所有点组成图形 G， ∴图形 G 为△ABC 的外接圆 ⊙ O， ∵BD 平分∠ABC， ∴∠ABD＝∠CBD， ∴ ＝ ， ∴AD＝CD； （2）如图，∵AD＝CM，AD＝CD， ∴CD＝CM， ∵DM⊥BC， ∴BC 垂直平分 DM， ∴BC 为直径， ∴∠BAC＝90°， ∵ ＝ ， ∴OD⊥AC， ∴OD∥AB， 第 7页（共 23页） ∵DE⊥AB， ∴OD⊥DE， ∴DE 为 ⊙ O 的切线， ∴直线 DE 与图形 G 的公共点个数为 1． 2．如图，AB 是 ⊙ O 的直径，过 ⊙ O 外一点 P 作 ⊙ O 的两条切线 PC，PD，切点分别为 C， D，连接 OP，CD． （1）求证：OP⊥CD； （2）连接 AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求 OP 的长． 【解答】解：（1）方法 1、连接 OC，OD， ∴OC＝OD， ∵PD，PC 是 ⊙ O 的切线， ∵∠ODP＝∠OCP＝90°， 在 Rt△ODP 和 Rt△OCP 中， ， ∴Rt△ODP≌Rt△OCP， ∴∠DOP＝∠COP， 第 8页（共 23页） ∵OD＝OC， ∴OP⊥CD； 方法 2、∵PD，PC 是 ⊙ O 的切线， ∴PD＝PC， ∵OD＝OC， ∴P，O 在 CD 的中垂线上， ∴OP⊥CD （2）如图，连接 OD，OC， ∴OA＝OD＝OC＝OB＝2， ∴∠ADO＝∠DAO＝50°，∠BCO＝∠CBO＝70°， ∴∠AOD＝80°，∠BOC＝40°， ∴∠COD＝60°， ∵OD＝OC， ∴△COD 是等边三角形， 由（1）知，∠DOP＝∠COP＝30°， 在 Rt△ODP 中，OP＝ ＝ ． 3．如图，AB 是 ⊙ O 的一条弦，E 是 AB 的中点，过点 E 作 EC⊥OA 于点 C，过点 B 作 ⊙ O 的切线交 CE 的延长线于点 D． （1）求证：DB＝DE； （2）若 AB＝12，BD＝5，求 ⊙ O 的半径． 第 9页（共 23页） 【解答】（1）证明：∵AO＝OB， ∴∠OAB＝∠OBA， ∵BD 是切线， ∴OB⊥BD， ∴∠OBD＝90°， ∴∠OBE+∠EBD＝90°， ∵EC⊥OA， ∴∠CAE+∠CEA＝90°， ∵∠CEA＝∠DEB， ∴∠EBD＝∠BED， ∴DB＝DE． （2）作 DF⊥AB 于 F，连接 OE． ∵DB＝DE，AE＝EB＝6， ∴EF＝ BE＝3，OE⊥AB， 在 Rt△EDF 中，DE＝BD＝5，EF＝3， ∴DF＝ ＝4， ∵∠AOE+∠A＝90°，∠DEF+∠A＝90°， ∴∠AOE＝∠DEF， ∴sin∠DEF＝sin∠AOE＝ ＝ ， ∵AE＝6， ∴AO＝ ． 第 10页（共 23页） ∴ ⊙ O 的半径为 ． 4．如图，AB 为 ⊙ O 的直径，F 为弦 AC 的中点，连接 OF 并延长交 于点 D，过点 D 作 ⊙ O 的切线，交 BA 的延长线于点 E． （1）求证：AC∥DE； （2）连接 CD，若 OA＝AE＝a，写出求四边形 ACDE 面积的思路． 【解答】（1）证明：∵ED 与 ⊙ O 相切于 D， ∴OD⊥DE， ∵F 为弦 AC 中点， ∴OD⊥AC， ∴AC∥DE． （2）解：作 DM⊥OA 于 M，连接 CD，CO，AD． 首先证明四边形 ACDE 是平行四边形，根据 S 平行四边形 ACDE＝AE•DM，只要求出 DM 即 可．（方法二：证明△ADE 的面积等于四边形 ACDE 的面积的一半） ∵AC∥DE，AE＝AO， ∴OF＝DF， ∵AF⊥DO， ∴AD＝AO， ∴AD＝AO＝OD， ∴△ADO 是等边三角形，同理△CDO 也是等边三角形， ∴∠CDO＝∠DOA＝60°，AE＝CD＝AD＝AO＝DO＝a， 第 11页（共 23页） ∴AO∥CD，又 AE＝CD， ∴四边形 ACDE 是平行四边形，易知 DM＝ a， ∴平行四边形 ACDE 面积＝ a2． 5．如图，AB 是 ⊙ O 的直径，过点 B 作 ⊙ O 的切线 BM，弦 CD∥BM，交 AB 于点 F，且 ＝ ，连接 AC，AD，延长 AD 交 BM 于点 E． （1）求证：△ACD 是等边三角形； （2）连接 OE，若 DE＝2，求 OE 的长． 【解答】（1）证明：∵AB 是 ⊙ O 的直径，BM 是 ⊙ O 的切线， ∴AB⊥BE， ∵CD∥BE， ∴CD⊥AB， ∴ ， ∵ ＝ ， ∴ ， ∴AD＝AC＝CD， ∴△ACD 是等边三角形； （2）解：连接 OE，过 O 作 ON⊥AD 于 N，由（1）知，△ACD 是等边三角形， 第 12页（共 23页） ∴∠DAC＝60° ∵AD＝AC，CD⊥AB， ∴∠DAB＝30°， ∴BE＝ AE，ON＝ AO， 设 ⊙ O 的半径为：r， ∴ON＝ r，AN＝DN＝ r， ∴EN＝2+ ，BE＝ AE＝ ， 在 Rt△NEO 与 Rt△BEO 中， OE2＝ON2+NE2＝OB2+BE2， 即（ ）2+（2+ ）2＝r2+ ， ∴r＝2 ， ∴OE2＝ +25＝28， ∴OE＝2 ． 6．如图，AB 是 ⊙ O 的直径，C 是 的中点， ⊙ O 的切线 BD 交 AC 的延长线于点 D，E 是 OB 的中点，CE 的延长线交切线 BD 于点 F，AF 交 ⊙ O 于点 H，连接 BH． （1）求证：AC＝CD； （2）若 OB＝2，求 BH 的长． 第 13页（共 23页） 【解答】（1）证明：连接 OC， ∵C 是 的中点，AB 是 ⊙ O 的直径， ∴CO⊥AB， ∵BD 是 ⊙ O 的切线， ∴BD⊥AB， ∴OC∥BD， ∵OA＝OB， ∴AC＝CD； （2）解：∵E 是 OB 的中点， ∴OE＝BE， 在△COE 和△FBE 中， ， ∴△COE≌△FBE（ASA）， ∴BF＝CO， ∵OB＝2， ∴BF＝2， ∴AF＝ ＝2 ， ∵AB 是直径， ∴BH⊥AF， ∴△ABF∽△BHF， 第 14页（共 23页） ∴ ＝ ， ∴AB•BF＝AF•BH， ∴BH＝ ＝ ＝ ． 7．如图 AB 是 ⊙ O 的直径，PA，PC 与 ⊙ O 分别相切于点 A，C，PC 交 AB 的延长线于点 D， DE⊥PO 交 PO 的延长线于点 E． （1）求证：∠EPD＝∠EDO； （2）若 PC＝6，tan∠PDA＝ ，求 OE 的长． 【解答】（1）证明：PA，PC 与 ⊙ O 分别相切于点 A，C， ∴∠APO＝∠EPD 且 PA⊥AO， ∴∠PAO＝90°， ∵∠AOP＝∠EOD，∠PAO＝∠E＝90°， ∴∠APO＝∠EDO， ∴∠EPD＝∠EDO； （2）解：连接 OC， ∴PA＝PC＝6， ∵tan∠PDA＝ ， 第 15页（共 23页） ∴在 Rt△PAD 中，AD＝8，PD＝10， ∴CD＝4， ∵tan∠PDA＝ ， ∴在 Rt△OCD 中，OC＝OA＝3，OD＝5， ∵∠EPD＝∠ODE， ∴△DEP∽△OED， ∴ ＝ ＝ ＝2， ∴DE＝2OE 在 Rt△OED 中，OE2+DE2＝OD2，即 5OE2＝52， ∴OE＝ ． 8．已知：如图，AB 是 ⊙ O 的直径，C 是 ⊙ O 上一点，OD⊥BC 于点 D，过点 C 作 ⊙ O 的切 线，交 OD 的延长线于点 E，连接 BE． （1）求证：BE 与 ⊙ O 相切； （2）连接 AD 并延长交 BE 于点 F，若 OB＝9，sin∠ABC＝ ，求 BF 的长． 【解答】证明：（1）连接 OC， 第 16页（共 23页） ∵OD⊥BC， ∴∠COE＝∠BOE， 在△OCE 和△OBE 中， ∵ ， ∴△OCE≌△OBE， ∴∠OBE＝∠OCE＝90°，即 OB⊥BE， ∵OB 是 ⊙ O 半径， ∴BE 与 ⊙ O 相切． （2）过点 D 作 DH⊥AB，连接 AD 并延长交 BE 于点 F， ∵∠DOH＝∠BOD，∠DHO＝∠BDO＝90°， ∴△ODH∽△OBD， ∴ ＝ ＝ 又∵sin∠ABC＝ ，OB＝9， ∴OD＝6， 易得∠ABC＝∠ODH， ∴sin∠ODH＝ ，即 ＝ ， ∴OH＝4， ∴DH＝ ＝2 ， 又∵△ADH∽△AFB， ∴ ＝ ， ＝ ， ∴FB＝ ． 第 17页（共 23页） 9．如图，在△ABC，AB＝AC，以 AB 为直径的 ⊙ O 分别交 AC、BC 于点 D、E，点 F 在 AC 的延长线上，且∠CBF＝ ∠CAB． （1）求证：直线 BF 是 ⊙ O 的切线； （2）若 AB＝5，sin∠CBF＝ ，求 BC 和 BF 的长． 【解答】（1）证明：连接 AE， ∵AB 是 ⊙ O 的直径， ∴∠AEB＝90°， ∴∠1+∠2＝90°． ∵AB＝AC， ∴∠1＝ ∠CAB． ∵∠CBF＝ ∠CAB， ∴∠1＝∠CBF ∴∠CBF+∠2＝90° 即∠ABF＝90° ∵AB 是 ⊙ O 的直径， ∴直线 BF 是 ⊙ O 的切线． （2）解：过点 C 作 CG⊥AB 于 G． ∵sin∠CBF＝ ，∠1＝∠CBF， ∴sin∠1＝ ， ∵在 Rt△AEB 中，∠AEB＝90°，AB＝5， ∴BE＝AB•sin∠1＝ ， ∵AB＝AC，∠AEB＝90°， 第 18页（共 23页） ∴BC＝2BE＝2 ， 在 Rt△ABE 中，由勾股定理得 AE＝ ＝2 ， ∴sin∠2＝ ＝ ＝ ，cos∠2＝ ＝ ＝ ， 在 Rt△CBG 中，可求得 GC＝4，GB＝2， ∴AG＝3， ∵GC∥BF， ∴△AGC∽△ABF， ∴ ∴BF＝ ＝ 10．已知：如图，在△ABC 中，D 是 AB 边上一点，圆 O 过 D、B、C 三点，∠DOC＝2∠ ACD＝90°． （1）求证：直线 AC 是圆 O 的切线； （2）如果∠ACB＝75°，圆 O 的半径为 2，求 BD 的长． 【解答】（1）证明：∵OD＝OC，∠DOC＝90°， ∴∠ODC＝∠OCD＝45°． ∵∠DOC＝2∠ACD＝90°， ∴∠ACD＝45°． ∴∠ACD+∠OCD＝∠OCA＝90°． ∵点 C 在圆 O 上， 第 19页（共 23页） ∴直线 AC 是圆 O 的切线． （2）解：方法 1：∵OD＝OC＝2，∠DOC＝90°， ∴CD＝2 ． ∵∠ACB＝75°，∠ACD＝45°， ∴∠BCD＝30°， 作 DE⊥BC 于点 E，则∠DEC＝90°， ∴DE＝DCsin30°＝ ． ∵∠B＝45°， ∴DB＝2． 方法 2：连接 BO ∵∠ACB＝75°，∠ACD＝45°， ∴∠BCD＝30°，∴∠BOD＝60° ∵OD＝OB＝2 ∴△BOD 是等边三角形 ∴BD＝OD＝2． 11．已知：如图，在△ABC 中，AB＝AC，AE 是角平分线，BM 平分∠ABC 交 AE 于点 M， 经过 B，M 两点的 ⊙ O 交 BC 于点 G，交 AB 于点 F，FB 恰为 ⊙ O 的直径． （1）求证：AE 与 ⊙ O 相切； （2）当 BC＝4，cosC＝ 时，求 ⊙ O 的半径． 第 20页（共 23页） 【解答】（1）证明：连接 OM，则 OM＝OB ∴∠1＝∠2 ∵BM 平分∠ABC ∴∠1＝∠3 ∴∠2＝∠3 ∴OM∥BC ∴∠AMO＝∠AEB 在△ABC 中，AB＝AC，AE 是角平分线 ∴AE⊥BC ∴∠AEB＝90° ∴∠AMO＝90° ∴OM⊥AE ∵点 M 在圆 O 上， ∴AE 与 ⊙ O 相切； （2）解：在△ABC 中，AB＝AC，AE 是角平分线 ∴BE＝ BC，∠ABC＝∠C ∵BC＝4，cosC＝ ∴BE＝2，cos∠ABC＝ 在△ABE 中，∠AEB＝90° ∴AB＝ ＝6 设 ⊙ O 的半径为 r，则 AO＝6﹣r ∵OM∥BC ∴△AOM∽△ABE 第 21页（共 23页） ∴ ∴ 解得 ∴ ⊙ O 的半径为 ． 12．已知：如图，在 Rt△ABC 中，∠C＝90°，点 O 在 AB 上，以 O 为圆心，OA 长为半径 的圆与 AC，AB 分别交于点 D，E，且∠CBD＝∠A． （1）判断直线 BD 与 ⊙ O 的位置关系，并证明你的结论； （2）若 AD：AO＝8：5，BC＝2，求 BD 的长． 【解答】解：（1）直线 BD 与 ⊙ O 相切． 证明：如图，连接 OD． ∵OA＝OD ∴∠A＝∠ADO ∵∠C＝90°，∴∠CBD+∠CDB＝90° 又∵∠CBD＝∠A ∴∠ADO+∠CDB＝90° ∴∠ODB＝90° ∴直线 BD 与 ⊙ O 相切． （2）解法一：如图，连接 DE． ∵AE 是 ⊙ O 的直径，∴∠ADE＝90° 第 22页（共 23页） ∵AD：AO＝8：5 ∴ ∵∠C＝90°，∠CBD＝∠A ∵BC＝2， ∴ 解法二：如图，过点 O 作 OH⊥AD 于点 H． ∴AH＝DH＝ ∵AD：AO＝8：5 ∴cosA＝ ∵∠C＝90°，∠CBD＝∠A ∴ ∵BC＝2 ∴ 第 23页（共 23页） 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2020/1/19 9:13:48 ；用户： 金雨教育；邮 箱：309593466@qq.com ；学号： 335385