- 2021-05-26 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教新课标A版高一数学3-3-2简单线性规划问题
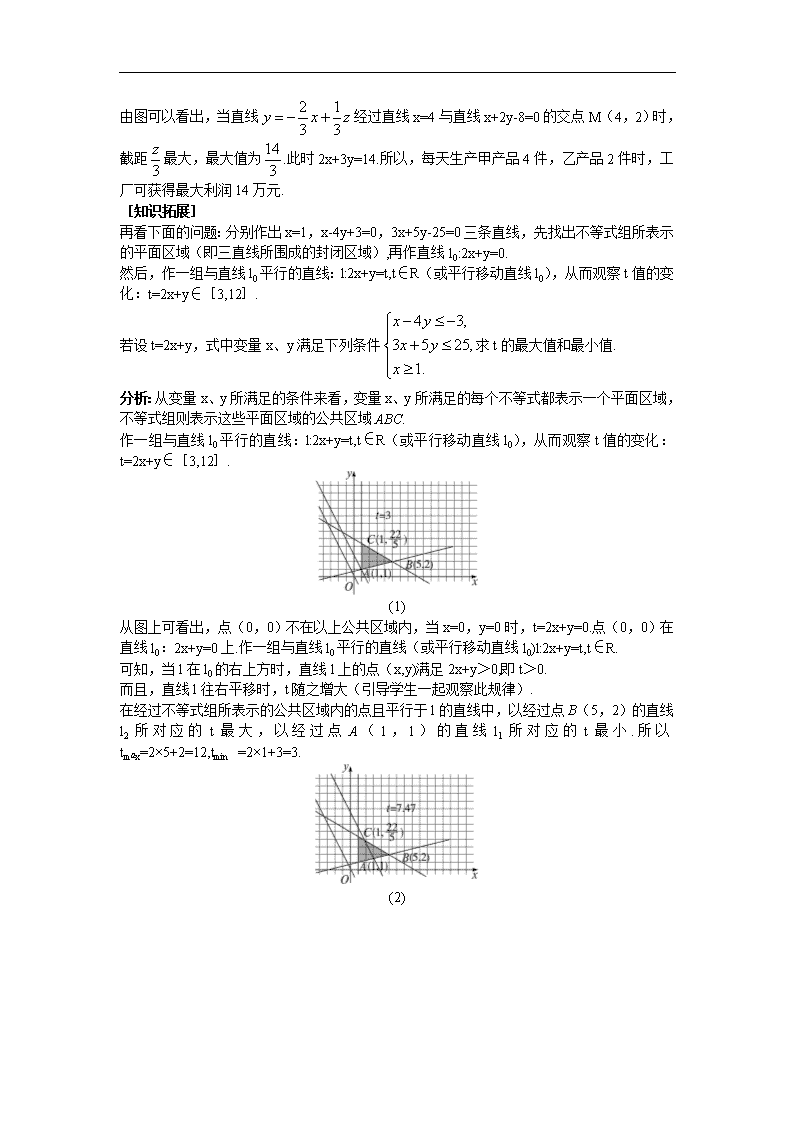
3.3.2 简单线性规划问题 从容说课 本节课先由师生共同分析日常生活中的实际问题来引出简单线性规划问题的一些基本 概念,由二元一次不等式组的解集可以表示为直角坐标平面上的区域引出问题:在直角坐标 系内,如何用二元一次不等式(组)的解集来解决直角坐标平面上的区域求解问题?再从一 个具体的二元一次不等式(组)入手,来研究一元二次不等式表示的区域及确定的方法,作 出其平面区域,并通过直线方程的知识得出最值.通过具体例题的分析和求解,在这些例题 中设置思考项,让学生探究,层层铺设,以便让学生更深刻地理解一元二次不等式表示的区 域的概念,有利于二元一次不等式(组)与平面区域的知识的巩固. “简单的线性规划”是在学生学习了直线方程的基础上,介绍直线方程的一个简单应用, 这是《新大纲》对数学知识应用的重视.线性规划是利用数学为工具,来研究一定的人、财、 物、时、空等资源在一定条件下,如何精打细算巧安排,用最少的资源,取得最大的经济效 益.它是数学规划中理论较完整、方法较成熟、应用较广泛的一个分支,并能解决科学研究、 工程设计、经营管理等许多方面的实际问题.中学所学的线性规划只是规划论中的极小一部 分,但这部分内容体现了数学的工具性、应用性,同时也渗透了化归、数形结合的数学思想, 为学生今后解决实际问题提供了一种重要的解题方法——数学建模法.通过这部分内容的学 习,可使学生进一步了解数学在解决实际问题中的应用,培养学生学习数学的兴趣和应用数 学的意识和解决实际问题的能力. 依据课程标准及教材分析,二元一次不等式表示平面区域以及线性规划的有关概念比较 抽象,按学生现有的知识和认知水平难以透彻理解,再加上学生对代数问题等价转化为几何 问题以及数学建模方法解决实际问题有一个学习消化的过程,故本节知识内容定为了解层 次. 本节内容渗透了多种数学思想,是向学生进行数学思想方法教学的好教材,也是培养学 生观察、作图等能力的好教材. 本节内容与实际问题联系紧密,有利于培养学生学习数学的兴趣和“用数学”的意识以及 解决实际问题的能力. 教学重点 重点是二元一次不等式(组)表示平面的区域. 教学难点 难点是把实际问题转化为线性规划问题,并给出解答.解决难点的关键是根据实际 问题中的已知条件,找出约束条件和目标函数,利用图解法求得最优解.为突出重点,本节 教学应指导学生紧紧抓住化归、数形结合的数学思想方法将实际问题数学化、代数问题几何 化. 课时安排 3 课时 三维目标 一、知识与技能 1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念; 2.运用线性规划问题的图解法,并能应用它解决一些简单的实际问题. 二、过程与方法 1.培养学生观察、联想以及作图的能力,渗透集合、化归、数形结合的数学思想,提高 学生“建模”和解决实际问题的能力; 2.结合教学内容,培养学生学习数学的兴趣和“用数学”的意识,激励学生创新. 三、情感态度与价值观 1.通过本节教学着重培养学生掌握“数形结合”的数学思想,尽管侧重于用“数”研究“形”, 但同时也用“形”去研究“数”,培养学生观察、联想、猜测、归纳等数学能力; 2.结合教学内容,培养学生学习数学的兴趣和“用数学”的意识,激励学生勇于创新. 教学过程 第 1 课时 导入新课 师 前面我们学习了二元一次不等式 Ax+By+C>0 在平面直角坐标系中的平面区域的确定方 法,请同学们回忆一下. (生回答) 推进新课 [合作探究] 师 在现实生产、生活中,经常会遇到资源利用、人力调配、生产安排等问题. 例如,某工厂用 A、B 两种配件生产甲、乙两种产品,每生产一件甲产品使用 4 个 A 产品耗 时 1 小时,每生产一件乙产品使用 4 个 B 产品耗时 2 小时,该厂每天最多可从配件厂获得 16 个 A 配件和 12 个 B 配件,按每天工作 8 小时计算,该厂所有可能的日生产安排是什么? 设甲、乙两种产品分别生产 x、y 件,应如何列式? 生 由已知条件可得二元一次不等式组: .0 ,0 ,124 ,164 ,82 y x y x yx 师 如何将上述不等式组表示成平面上的区域? 生 (板演) 师 对照课本 98 页图 3.39,图中阴影部分中的整点(坐标为整数的点)就代表所有可能的日 生产安排,即当点 P(x,y)在上述平面区域中时,所安排的生产任务 x、y 才有意义. 进一步,若生产一件甲产品获利 2 万元,生产一件乙产品获利 3 万元,采用哪种生产安排利 润最大? 设生产甲产品 x 件,乙产品 y 件时,工厂获得利润为 z,则如何表示它们的关系? 生 则 z=2x+3y. 师 这样,上述问题就转化为:当 x、y 满足上述不等式组并且为非负整数时,z 的最大值是 多少? [教师精讲] 师 把 z=2x+3y 变形为 zxy 3 1 3 2 ,这是斜率为 3 2 ,在 y 轴上的截距为 3 1 z 的直线.当 z 变化时可以得到什么样的图形?在上图中表示出来. 生 当 z 变化时可以得到一组互相平行的直线.(板演) 师 由于这些直线的斜率是确定的,因此只要给定一个点〔例如(1,2)〕,就能确定一条直 线 zxy 3 1 3 2 ,这说明,截距 z[]3 可以由平面内的一个点的坐标唯一确定.可以看到直 线 zxy 3 1 3 2 与表示不等式组的区域的交点坐标满足不等式组,而且当截距 3 z 最大时, z 取最大值,因此,问题转化为当直线 zxy 3 1 3 2 与不等式组确定的区域有公共点时, 可以在区域内找一个点 P,使直线经过 P 时截距 3 z 最大. 由图可以看出,当直线 zxy 3 1 3 2 经过直线 x=4 与直线 x+2y-8=0 的交点 M(4,2)时, 截距 3 z 最大,最大值为 3 14 .此时 2x+3y=14.所以,每天生产甲产品 4 件,乙产品 2 件时,工 厂可获得最大利润 14 万元. [知识拓展] 再看下面的问题:分别作出 x=1,x-4y+3=0,3x+5y-25=0 三条直线,先找出不等式组所表示 的平面区域(即三直线所围成的封闭区域),再作直线 l0:2x+y=0. 然后,作一组与直线 l0 平行的直线:l:2x+y=t,t∈R(或平行移动直线 l0),从而观察 t 值的变 化:t=2x+y∈[3,12]. 若设 t=2x+y,式中变量 x、y 满足下列条件 .1 ,2553 ,34 x yx yx 求 t 的最大值和最小值. 分析:从变量 x、y 所满足的条件来看,变量 x、y 所满足的每个不等式都表示一个平面区域, 不等式组则表示这些平面区域的公共区域 ABC. 作一组与直线 l0 平行的直线:l:2x+y=t,t∈R(或平行移动直线 l0),从而观察 t 值的变化: t=2x+y∈[3,12]. (1) 从图上可看出,点(0,0)不在以上公共区域内,当 x=0,y=0 时,t=2x+y=0.点(0,0)在 直线 l0:2x+y=0 上.作一组与直线 l0 平行的直线(或平行移动直线 l0)l:2x+y=t,t∈R. 可知,当 l 在 l0 的右上方时,直线 l 上的点(x,y)满足 2x+y>0,即 t>0. 而且,直线 l 往右平移时,t 随之增大(引导学生一起观察此规律). 在经过不等式组所表示的公共区域内的点且平行于 l 的直线中,以经过点 B(5,2)的直线 l2 所 对 应 的 t 最 大 , 以 经 过 点 A ( 1 , 1 ) 的 直 线 l1 所 对 应 的 t 最 小 . 所 以 tmax=2×5+2=12,tmin =2×1+3=3. (2) (3) [合作探究] 师 诸如上述问题中,不等式组是一组对变量 x、y 的约束条件,由于这组约束条件都是关于 x、y 的一次不等式,所以又可称其为线性约束条件.t=2x+y 是欲达到最大值或最小值所涉及 的变量 x、y 的解析式,我们把它称为目标函数.由于 t=2x+y 又是关于 x、y 的一次解析式, 所以又可叫做线性目标函数. 另外注意:线性约束条件除了用一次不等式表示外,也可用一次方程表示. 一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题. 例如:我们刚才研究的就是求线性目标函数 z=2x+y 在线性约束条件下的最大值和最小值的 问题,即为线性规划问题. 那么,满足线性约束条件的解(x,y)叫做可行解,由所有可行解组成的集合叫做可行域.在上 述问题中,可行域就是阴影部分表示的三角形区域.其中可行解(5,2)和(1,1)分别使 目标函数取得最大值和最小值,它们都叫做这个问题的最优解. 课堂小结 用图解法解决简单的线性规划问题的基本步骤: 1.首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域). 2.设 t=0,画出直线 l0. 3.观察、分析,平移直线 l0,从而找到最优解. 4.最后求得目标函数的最大值及最小值. 布置作业 1.某工厂用两种不同原料均可生产同一产品,若采用甲种原料,每吨成本 1 000 元,运费 500 元,可得产品 90 千克;若采用乙种原料,每吨成本为 1500 元,运费 400 元,可得产品 100 千克,如果每月原料的总成本不超过 6 000 元,运费不超过 2 000 元,那么此工厂每月最多 可生产多少千克产品? 分析:将已知数据列成下表: 甲原料(吨) 乙原料(吨) 费用限额 成本 1 000 1 500 6 000 运费 500 400 2 000 产品 90 100 解:设此工厂每月甲、乙两种原料各 x 吨、y 吨,生产 z 千克产品,则 ,2000400500 ,600015001000 ,0 ,0 yx yx y x z=90x+100y. 作出以上不等式组所表示的平面区域,即可行域,如右图: 由 .2045 ,1232 yx yx 得 .7 20 ,7 12 y x 令 90x+100y=t,作直线:90x+100y=0,即 9x+10y=0 的平行线 90x+100y=t,当 90x+100y=t 过 点 M( 7 12 , 7 20 )时,直线 90x+100y=t 中的截距最大. 由此得出 t 的值也最大,zmax =90× 7 12 +100× 7 20 =440. 答:工厂每月生产 440 千克产品. 2.某工厂家具车间造 A、B 型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一 张 A、B 型桌子分别需要 1 小时和 2 小时,漆工油漆一张 A、B 型桌子分别需要 3 小时和 1 小时;又知木工、漆工每天工作分别不得超过 8 小时和 9 小时,而工厂造一张 A、B 型桌子 分别获利润 2 千元和 3 千元,试问工厂每天应生产 A、B 型桌子各多少张,才能获得利润最 大? 解:设每天生产 A 型桌子 x 张,B 型桌子 y 张, 则 .0,0 ,93 ,82 yx yx yx 目标函数为 z=2x+3y. 作出可行域: 把直线 l:2x+3y=0 向右上方平移至 l′的位置时,直线经过可行域上的点 M,且与原点距离 最大,此时 z=2x+3y 取得最大值. 解方程 ,93 ,82 yx yx 得 M 的坐标为(2,3). 答:每天应生产 A 型桌子 2 张,B 型桌子 3 张才能获得最大利润. 3.课本 106 页习题 3.3A 组 2. 第 2 课时 导入新课 师 前面我们学习了目标函数、线性目标函数、线性规划问题、可行解、可行域、最优解等 概念. 师 同学们回忆一下用图解法解决简单的线性规划问题的基本步骤. 生(1)首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域); (2)设 t=0,画出直线 l0; (3)观察、分析,平移直线 l0,从而找到最优解; (4)最后求得目标函数的最大值及最小值. 推进新课 师 【例 1】 已知 x、y 满足不等式组 ,0 ,0 ,2502 ,3002 y x yx yx 试求 z=300x+900y 的最大值时的整点 的坐标及相应的 z 的最大值. 师 分析:先画出平面区域,然后在平面区域内寻找使 z=300x+900y 取最大值时的整点. 解:如图所示平面区域 AOBC,点 A(0,125),点 B(150,0),点 C 的坐标由方程组 2502 3002 yx yx ,3 200 ,3 350 y x 得 C( 3 350 , 3 200 ), 令 t=300x+900y, 即 ,9003 1 txy , 欲求 z=300x+900y 的最大值,即转化为求截距 t[]900 的最大值,从而可求 t 的最大值,因直 线 9003 1 txy 与直线 xy 3 1 平行,故作 xy 3 1 的平行线,当过点 A(0,125)时, 对应的直线的截距最大,所以此时整点 A 使 z 取最大值,zmax=300×0+900×125=112 500. 师 【例 2】 求 z=600x+300y 的最大值,使式中的 x、y 满足约束条件 3x+y≤300,x+2y≤250, x≥0,y≥0 的整数值. 师 分析:画出约束条件表示的平面区域即可行域再解. 解:可行域如图所示. 四边形 AOBC,易求点 A(0,126),B(100,0),由方程组 2522 3003 yx yx .5 191 ,5 369 y x 得点 C 的坐标为( 5 369 , 5 191 ). 因题设条件要求整点(x,y)使 z=600x+300y 取最大值,将点(69,91),(70,90)代入 z=600x+300y,可知当 x=70, y=90 时,z 取最大值为 zmax=600×70+300×900=69 000. 师 【例 3】 已知 x、y 满足不等式 ,0,0 ,12 ,22 yx yx yx 求 z=3x+y 的最小值. 师 分析:可先找出可行域,平行移动直线 l0:3x+y=0 找出可行解,进而求出目标函数的最小 值. 解:不等式 x+2y≥2 表示直线 x+2y=2 上及其右上方的点的集合; 不等式 2x+y≥1 表示直线 2x+y=1 上及其右上方的点的集合. 可行域如右图所示. 作直线 l0:3x+y=0,作一组与直线 l0 平行的直线 l:3x+y=t(t∈R). ∵x、y 是上面不等式组表示的区域内的点的坐标. 由图可知: 当直线 l:3x+y=t 通过 P(0,1)时,t 取到最小值 1,即 z min=1. 师 评述:简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题 目是以什么实际问题提出,其求解的格式与步骤是不变的: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域作出可行域; (3)在可行域内求目标函数的最优解. 师 课堂练习:请同学们通过完成练习来掌握图解法解决简单的线性规划问题. (1)求 z=2x+y 的最大值,使式中的 x、y 满足约束条件 .1 ,1 , y yx xy (2)求 z=3x+5y 的最大值和最小值,使式中的 x、y 满足约束条件 .35 ,1 ,1535 yx xy yx [教师精讲] 师 (1)求 z=2x+y 的最大值,使式中的 x、y 满足约束条件 .1 ,1 , y yx xy 解:不等式组表示的平面区域如右图所示: 当 x=0,y=0 时,z=2x+y=0, 点(0,0)在直线 l0:2x+y=0 上. 作一组与直线 l0 平行的直线 l:2x+y=t,t∈R. 可知在经过不等式组所表示的公共区域内的点且平行于 l 的直线中,以经过点 A(2,-1)的 直线所对应的 t 最大. 所以 z max=2×2-1=3. (2)求 z=3x+5y 的最大值和最小值,使式中的 x、y 满足约束条件 .35 ,1 ,1535 yx xy yx 解:不等式组所表示的平面区域如右图所示. 从图示可知直线 3x+5y=t 在经过不等式组所表示的公共区域内的点时,以经过点(-2,-1) 的直线所对应的 t 最小,以经过点( 8 9 , 8 17 )的直线所对应的 t 最大. 所以 z min=3×(-2)+5×(-1)=-11,z max=3× 8 9 +5× 8 17 =14. [知识拓展] 某工厂生产甲、乙两种产品.已知生产甲种产品 1 t,需耗 A 种矿石 10 t、B 种矿石 5 t、煤 4 t; 生产乙种产品需耗 A 种矿石 4 t、B 种矿石 4 t、煤 9 t.每 1 t 甲种产品的利润是 600 元,每 1 t 乙种产品的利润是 1 000 元.工厂在生产这两种产品的计划中要求消耗 A 种矿石不超过 360 t、 B 种矿石不超过 200 t、煤不超过 300 t,甲、乙两种产品应各生产多少(精确到 0.1 t),能使 利润总额达到最大? 师 分析:将已知数据列成下表: 消耗量 产品 资源 甲产品(1 t) 乙产品(1 t) 资源限额(t) A 种矿石(t) 10 4 300 B 种矿石(t) 5 4 200 煤(t) 利润(元) 4 9 360 600 1 000 解:设生产甲、乙两种产品分别为 x t、y t,利润总额为 z 元, 那么 ;0 ,0 ,36094 ,20045 ,300410 y x yx yx yx 目标函数为 z=600x+1 000y. 作出以上不等式组所表示的平面区域,即可行域. 作直线 l:600x+1 000y=0, 即直线:3x+5y=0, 把直线 l 向右上方平移至 l1 的位置时,直线经过可行域上的点 M,且与原点距离最大,此时 z=600x+1 000y 取最大值. 解方程组 ,36094 ,20045 yx yx 得 M 的坐标为 x= 29 360 ≈12.4,y= 29 1000 ≈34.4. 答:应生产甲产品约 12.4 t,乙产品 34.4 t,能使利润总额达到最大. 课堂小结 用图解法解决简单的线性规划问题的基本步骤: (1)首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域). (2)设 t=0,画出直线 l0. (3)观察、分析,平移直线 l0,从而找到最优解. (4)最后求得目标函数的最大值及最小值. 以实际问题为背景的线性规划问题其求解的格式与步骤: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域作出可行域; (3)在可行域内求目标函数的最优解. 当然也要注意问题的实际意义 布置作业 课本第 105 页习题 3.3A 组 3、4. 第 3 课时 导入新课 师 前面我们已经学习了 用图解法解决简单的线性规划问题的基本步骤以及以实际问题为背景的线性规划问题其求 解的格式与步骤.这节课我们继续来看它们的实际应用问题. 推进新课 师 【例 5】 营养学家指出,成人良好的日常饮食应该至少提供 0.075 kg 的碳水化合物,0.06 kg 的蛋白质,0.06 kg 的脂肪.1 kg 食物 A 含有 0.105 kg 碳水化合物,0.07 kg 蛋白质,0.14 kg 脂肪,花费 28 元;而 1kg 食物 B 含有 0.105 kg 碳水化合物,0.14 kg 蛋白质,0.07 kg 脂肪, 花费 21 元.为了满足营养学家指出的日常饮食要求,同时使花费最低,需要同时食用食物 A 和食物 B 各多少克? 师 分析:将已知数据列成下表: 食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg A 0.105 0.07 0.14 B 0.105 0.14 0.07 若设每天食用 x kg 食物 A,y kg 食物 B,总成本为 z,如何列式? 生 由题设条件列出约束条件 ① 0,y 0,x 0.06,0.07y0.14x 0.06,0.14y0.07x 0.075,0.105y105x.0 其目标函数 z=28x+21y. 二元一次不等式组①等价于 ② .0 ,0 ,6714 ,6147 ,577 y x yx yx yx 师 作出二元一次不等式组②所表示的平面区域,即可行域.请同学们在草稿纸上完成,再与 课本上的对照. 生 考虑 z=28x+21y,将它变形为 283 4 zxy ,这是斜率为 3 4- 、随 z 变化的一族平行直 线. 28 z 是直线在 y 轴上的截距,当 28 z 取得最小值时,z 的值最小.当然直线与可行域相交, 即在满足约束条件时目标函数 z=28x+21y 取得最小值. 由图可见,当直线 z=28x+21y 经过可行域上的点 M 时,截距 z[]28 最小,即 z 最小. 解方程组 6714 ,577 yx yx 得点 M( 7 1 , 7 4 ),因此,当 7 1x , 7 4y 时,z=28x+21y 取最小值, 最小值为 16. 由此可知每天食用食物 A 约 143 克,食物 B 约 571 克,能够满足日常饮食要求,又使花费 最低,最低成本为 16 元. 师 【例 6】 在上一节课本的例题(课本 95 页例 3)中,若根据有关部门的规定,初中每人 每年可收取学费 1 600 元,高中每人每年可收取学费 2 700 元.那么开设初中班和高中班各多 少个,每年收取的学费总额最多? 学段 班级学生数 配备教师数 硬件建设/万元 教师年薪/万元 初中 45 2 26/班 2/人 高中 40 3 54/班 2/人 师 由前面内容知若设开设初中班 x 个,高中班 y 个,收取的学费总额为 z 万元, 此时,目标函数 z=0.16×45x+0.27×40y,可行域如下图 把 z=7.2x+10.8y 变形为 54 5 3 2 zxy ,得到斜率为- 3 2- ,在 y 轴上截距为 54 5z ,随 z 变化 的一组平行直线. 由图可以看出,当直线 z=7.2x+10.8y 经过可行域上的点 M 时,截距 54 5z 最大,即 z 最大. 解方程组 402 ,30 yx yx 得点 M(20,10),因此,当 x=20,y=10 时,z=7.2x+10.8y 取最大值, 最大值为 252. 由此可知开设 20 个初中班和 10 个高中班时,每年收取的学费总额最多,为 252 万元. 师 【例 7】 在上一节例 4 中(课本 96 页例 4),若生产 1 车皮甲种肥料,产生的利润为 10 000 元,若生产 1 车皮乙种肥料,产生的利润为 5 000 元,那么分别生产甲、乙两种肥料各 多少车皮,能够产生最大的利润? 生 若设生产 x 车皮甲种肥料,y 车皮乙种肥料,能够产生的利润 z 万元.目标函数 z= x+0.5y,可行域如下图: 把 z=x+0.5y 变形为 y=-2x+2z,得到斜率为-2,在 y 轴上截距为 2z,随 z 变化的一组平行直线. 由图可以看出,当直线 y=-2x+2z 经过可行域上的点 M 时,截距 2z 最大,即 z 最大. 解方程组 104 ,661518 yx yx 得点 M(2,2),因此当 x=2,y=2 时,z=x+0.5y 取最大值,最大值为 3. 由此可见,生产甲、乙两种肥料各 2 车皮,能够产生最大的利润,最大利润为 3 万元. [教师精讲] 师 以实际问题为背景的线性规划问题其求解的格式与步骤: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域做出可行域; (3)在可行域内求目标函数的最优解. 当然也要注意问题的实际意义. 课堂小结 用图解法解决简单的线性规划问题的基本步骤: (1)首先,要根据线性约束条件画出可行域(即画出不等式组所表示的公共区域); (2)设 t=0,画出直线 l0; (3)观察、分析,平移直线 l0,从而找到最优解; (4)最后求得目标函数的最大值及最小值. 以实际问题为背景的线性规划问题其求解的格式与步骤: (1)寻找线性约束条件,线性目标函数; (2)由二元一次不等式表示的平面区域做出可行域; (3)在可行域内求目标函数的最优解. 当然也要注意问题的实际意义. 布置作业 课本第 105 页习题 3.3 B 组 1、2、3 板书设计 第 1 课时 简单线性规划问题 图 1 课堂小结 线性规划问题的相关概念 图 2 第 2 课时 简单线性规划问题 例 1 课堂小结 例 3 例 2 第 3 课时 简单线性规划问题 例 5 课堂小结 例 7 例 6查看更多