高考高职单招数学模拟试题及答案word版 (16)

高考高职单招数学模拟试题及答案word版 (16)

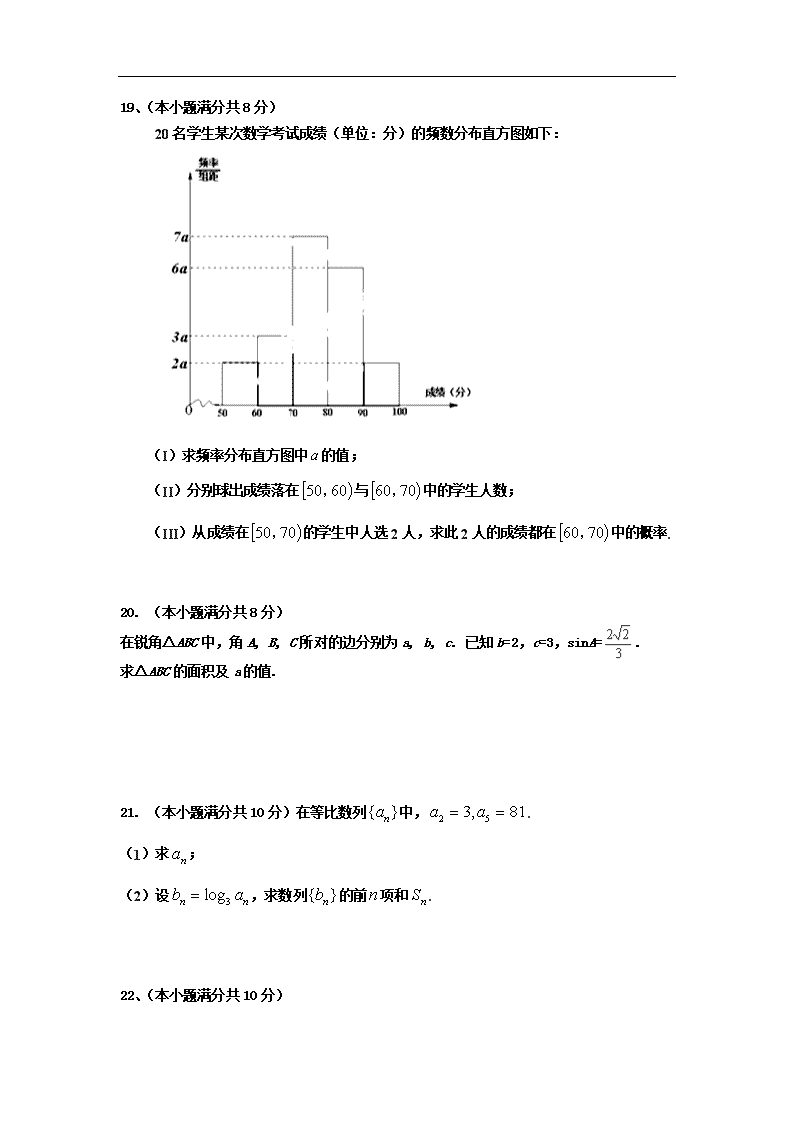
福建省高考高职单招数学模拟试题 一、选择题：本大题共 14 个小题，每小题 5 分，共 70 分。在每小题给出的四个选项中， 只有一项符合题目要求，请将答案填写在答题卡上. 1、.若集合 A＝ 0,1,2,4 ，B＝ 1,2,3 ，则 BA  =（ ） A. 0,1,2,3,4 B. 0,4 C. 1,2 D. 3 2.不等式 032  xx 的解集是（ ） A． )0,( B． )3,0( C． ( ,0) (3, )  D． ),3(  3.函数 1 1)(   x xf 的定义域为（ ） A. }1|{ xx B. }1|{ xx C. }0|{  xRx D. }1|{  xRx 4.已知等差数列{ }na 的前 n 项和 nS ，若 1854  aa ，则 8S = （ ） A.72 B. 68 C. 54 D. 90 5．圆 2 2( 1) 3x y   的圆心坐标和半径分别是（ ） (A) ( 1,0),3 (B) (1,0),3 (C) ( 1,0), 3 (D) (1,0), 3 6.已知命题 : ,sin 1,p x R x   则 p 是（ ）. （ A ） ,sin 1x R x   （ B ） ,sin 1x R x   （ C ） ,sin 1x R x   （ D ） ,sin 1x R x   7.若 a R ，则 0a  是  1 0a a   的（ ） A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分又不必要条件 8.下列函数 )(xf 中，在  ,0 上为增函数的是（ ） A. xxf 1)(  B. 2)1()(  xxf C xxf ln)(  D. x xf      2 1)( 9.设 ( )f x 是定义在 R 上的奇函数，当 0x  时， 2( ) 2f x x x  ，则 (1)f  ( ) A. 3 B. 1 C.１ D.3 10.过点 A(2,3)且垂直于直线 2x+y-5=0 的直线方程为( A ) (A)x-2y+4=0 (B)2x+y-7=0 (C)x-2y+3=0 (D)x-2y+5=0 11． 0000 167cos43sin77cos43cos  的值为（ ） A、1 B、 1 C、 2 1 D、 2 1 12．函数 2log , (0,16]y x x  的值域是（ ） .( , 4]A   .( ,4]B  .[ 4, )C   .[4, )D  13、已知函数   123  xxxxf ，则  xf 在（0，1）处的切线方程为（ ） A、 01  yx B、 01  yx C、 01  yx D、 01  yx 14.如图，F1，F2 是双曲线 C1： 13 2 2  yx 与椭圆 C2 的公共焦点，点 A 是 C1，C2 在第一象限 的公共点．若|F1F2|＝|F1A|，则 C2 的离心率是（ ） A． 3 1 B． 3 2 C. 3 2 或 5 2 D． 5 2 14 题 二、 填空题：本大题共 4 个小题，每小题 5 分，共 20 分。请把答案写在答题卡相应的位 置上. 15、函数 (2 )xy a  在定义域内是减函数，则 a 的取值范围是 16.已知角α的顶点在原点,始边与 x 轴非负半轴重合,与单位圆的交点为 P(- 5 4 , 5 3 )是α终 边上一点,则 sin α= . 17 、 已 知 椭 圆 的 方 程 为 164 22  yx ， 若 P 是 椭 圆 上 一 点 ， 且 ,7|| 1 PF 则 2PF = . 18. 某产品的广告费用 x 与销售额 y 的统计数据如下表： 广告费用 x(万元) 4 2 3 5 销售额 y(万元) 49 26 39 54 根据上表可得回归方程y^＝b^x＋a^中的b^为 9.4，据此模型预报广告费用为 6 万元时销售额 为 三、解答题（本大题共 5 小题，共 60 分.解答应写出文字说明，证明过程或演算步骤） 19、（本小题满分共 8 分） 20 名学生某次数学考试成绩（单位：分）的频数分布直方图如下： （I）求频率分布直方图中 a 的值； （II）分别球出成绩落在 6050， 与 7060， 中的学生人数； （III）从成绩在 7050， 的学生中人选 2 人，求此 2 人的成绩都在 7060， 中的概率. 20. （本小题满分共 8 分） 在锐角△ABC 中，角 A, B, C 所对的边分别为 a, b, c. 已知 b=2，c=3，sinA= 3 22 . 求△ABC 的面积及 a 的值. 21. （本小题满分共 10 分）在等比数列{ }na 中， 2 53, 81a a  . （1）求 na ； （2）设 3logn nb a ，求数列{ }nb 的前 n 项和 nS . 22、（本小题满分共 10 分） 如图，四棱锥 P—ABCD 中，PD  平面 ABCD，底面 ABCD 为矩形，PD=DC=4，AD=2，E 为 PC 的中点。 （1）求证：AD⊥PC； （2）在线段 AC 上是否存在一点 M，使得 PA//平面 EDM，若存在，求出 AM 的长；若 不存在，请说明理由. 23. （本小题满分共 12 分） 已知 a，b 为常数，且 a≠0，函数 f(x)＝－ax＋b＋axln x，f(e)＝2 (1)求实数 b 的值；(2)求函数 f(x)的单调区间； 24、（本小题满分共 12 分） 如 图 6 ， 已 知 圆 2 2: 2 2 0G x y x y    经 过 椭 圆 2 2 2 2 1( 0)x y a ba b     的右焦点 F 及上顶点 B ，过椭圆 外一点  ,0m  m a 且倾斜角为 5 6  的直线 l 交椭圆 于 ,C D 两点． （I）求椭圆的方程； （Ⅱ）若 0,FC FD   求 m 的值． ( ,0)mF B x y D C O 答案及解析： 请将选择题答案填入下表： 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 得分 选项 C B B A D C A C A A D B C B 14.B 由双曲线的方程可知 ， ，由双曲线的定义 可知 ，所以由椭圆的定义知 ，所以 ．  1,2 5 3 1 19. 【答案】（I） 0.005a  ；（II）2,3；（III） 3 10 . 20. 223 22322 1sin2 1  AbcS ABC 3 21. (1) 13n na  .（2） 2 2n n nS  . 22       62sin2 x 单调递増区间为       kk 6,3 ， Zk  23 （Ⅱ） 设{ }nb 的公差为 d ，则有 1 1 3 8, 15 32, b d b d      解得 1 2, 2. b d    则数列{ }nb 的前 n 项和 1 ( 1) 2n n nS nb d  2( 1)2 2 .2 n nn n n     分 24. 解：（I）∵圆 022: 22  yxyxG 经过点 F，B， ∴F（2,0），B（0 2 ）， ∴ ,2,2  bc ∴ .62 a 故椭圆的方程为 .126 22  yx ．…………………6 分 （Ⅱ）由题意得直线 l 的方程为 ).6)((3 3  mmxy 由 .0622 )(3 3 126 22 22          mmxxy mxy yx 得消去 由△ ,0)6(84 22  mm 解得 .3232  m 又 .326,6  mm ……………………8 分 设 ),,(),,( 2211 yxDyxC 则 ,2 6, 2 2121  mxxmxx ∴ .3)(33 1)(3 3)(3 3 2 21212121 mxxmxxmxmxyy              ∵ ),,2(),,2( 2211 yxFDyxFC  ………………………10 分 .3 )3(243)(3 6 3 4)2)(2( 2 21212121  mmmxxmxxyyxxFDFC ∵ ,03 )3(2,0FDFC  mm即 解得 .3,32630  mmmm ，又或 ……………………14 分