- 2021-05-25 发布 |
- 37.5 KB |
- 7页
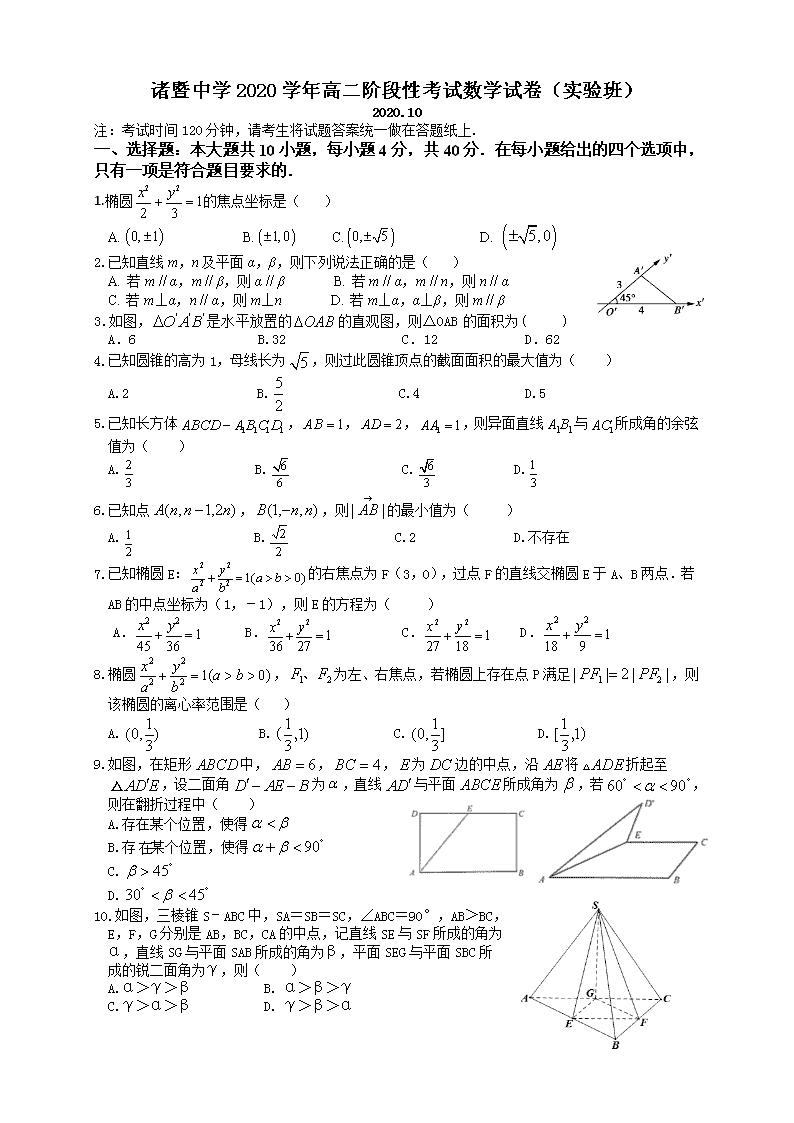


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省诸暨中学2020-2021高二数学10月阶段性试题(实验班)(Word版附答案)
诸暨中学2020学年高二阶段性考试数学试卷(实验班) 2020.10 注:考试时间120分钟,请考生将试题答案统一做在答题纸上. 一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.椭圆的焦点坐标是( ) A. B. C. D. 2.已知直线m,n及平面α,β,则下列说法正确的是( ) A. 若mα,mβ,则αβ B. 若mα,mn,则nα C. 若m⊥α,nα,则m⊥n D. 若m⊥α,α⊥β,则mβ 3.如图,是水平放置的的直观图,则△OAB 的面积为( ) A.6 B.32 C.12 D.62 4.已知圆锥的高为1,母线长为,则过此圆锥顶点的截面面积的最大值为( ) A.2 B. C.4 D.5 5.已知长方体,,,,则异面直线与所成角的余弦值为( ) A. B. C. D. 6.已知点,,则的最小值为( ) A. B. C.2 D.不存在 7.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为( ) A. B. C. D. 8.椭圆,为左、右焦点,若椭圆上存在点P满足,则该椭圆的离心率范围是( ) A. B. C. D. 9.如图,在矩形中,,,为边的中点,沿将折起至,设二面角为,直线与平面所成角为,若,则在翻折过程中( ) A.存在某个位置,使得 B.存某个位置,使得 C. D. 10.如图,三棱锥S﹣ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,CA的中点,记直线SE与SF所成的角为α,直线SG与平面SAB所成的角为β,平面SEG与平面SBC所成的锐二面角为γ,则( ) A.α>γ>β B. α>β>γ C.γ>α>β D. γ>β>α 二、填空题:本大题共7小题,每空3分,共30分. 11.已知椭圆中心在原点,一个焦点为,且长轴长是短轴长的倍,则该椭圆的长轴长为 ,其标准方程是 . 12.已知为椭圆的左、右焦点,是椭圆上一点, 若,则等于 . 13. 如图,网格纸上小正方形边长为,粗线画出的是某几何 体的三视图,则该几何体的体积为 ,该几何体外接球的 表面积为 . 14.已知线段AB的长度是10,它的两个端点分别在x轴、y轴上滑动,则AB的中点P的轨迹方程是 . 15.在二面角中,,且,, 若 ,,二面角的余弦值为,则 ; 直线与平面所成角正弦值为 . 16.已知椭圆的离心率,是椭圆的左、右顶点,点是椭圆上不同于的一点,直线的倾斜角分别为,则 . 17.如图,正四面体ABCD的棱CD在平面内,E为棱BC的中点, 当 正四面体ABCD绕CD旋转时,直线AE与平面所成最大角的正 弦值为 . 三、解答题:本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤. 18.(本题满分12分)如图,在四棱锥中,,,, ,. (Ⅰ)求证:平面⊥平面; (Ⅱ)求直线与平面所成角的正弦值. 19. (本题满分12分)已知椭圆,若椭圆C的离心率为. (1)求的值; (2)若过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得?若存在,求出点的坐标;若不存在,请说明理由. 20.(本题满分13分)在如图所示的几何体中,四边形为矩形,平面平面,//,,,,点在棱上. (Ⅰ)若为的中点,求证://平面; (Ⅱ)若二面角的余弦值为,求的长度. 21.(本题满分13分)椭圆C:(a>b>0)的离心率为,且过点,点P为椭圆C上的动点,且在第四象限,A为左顶点,B为上顶点,PA交y轴于点C,PB交x轴于点D. (Ⅰ)求椭圆C的标准方程; (Ⅱ)求△PCD的面积的最大值. 诸暨中学2020学年高二阶段性考试数学答案(实验班) 一、 选择题(每题4分) ACCBB BDDDA 二、 填空题(每空3分) 三、解答题 18(Ⅰ)取中点E ,为中点,. ,∴,且,即有四边形是矩形. ∴.又,,∴. 而,∴平面,又平面,∴平面⊥平面(6分) (Ⅱ)以A 为原点,所在直线为轴,所在直线为轴,建立空间直角坐标角系,如图所示: , 则 ∴. 设平面法向量为,则, 取,得.(12分) 设直线与平面所成的角为,. 直线与平面所成的角的正弦值为. 20.(Ⅰ)因为a2=2,b2=n,所以c2=2-n,,(4分) ( II)若存在点M(m,0),使得∠NMA+∠NMB=180°,则直线AM和BM的斜率存在,分别设为k1,k2.等价于k1+k2=0.依题意,直线l的斜率存在,故设直线l的方程为y=k(x+2).由得:(2k2+1)x2+8k2x+8k2-2=0.因为直线l与椭圆C有两个交点,所以△>0. 即(8k2)2-4(2k2+1)(8k2-2)>0,解得. 设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=.(7分) y1=k(x1+2),y2=k(x2+2). 令k1+k2==0,(x1-m)y2+(x2-m)y1=0,(9分) (x1-m)k(x2+2)+(x2-m)k(x1+2)=0, 当k≠0时,2x1x2-(m-2)(x1+x2)-4m=0,∴m=-1. 当k=0时,也成立. 所以存在点M(-1,0),使得∠PQM+∠PQN=180°.(12分) 20.(Ⅰ)证明:连接BD,交AC于点O,连接OP.因为P是DF中点,O为矩形ABCD 对角线的交点,所以OP为三角形BDF中位线,所以BF // OP, 因为BF平面ACP,OP平面ACP,所以BF // 平面ACP.(6分) (Ⅱ)因为∠BAF=90º,所以AF⊥AB,又因为平面ABEF⊥平面ABCD,且平面ABEF ∩平面ABCD= AB,所以AF⊥平面ABCD.从而AF⊥CD又因为四边形ABCD为矩形,所以AD⊥CD,从而CD⊥平面FAD,所以∠CPD就是直线PC与平面FAD所成的角. 又, 且.(13分) 21(1) 由题意得:得a2=4,b2=1, 故椭圆C的标准方程为:+y2=1.(5分) (2) 由题意设lAP:y=k(x+2),-查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档