- 2021-05-25 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海数学中考 一模填空题汇总复习
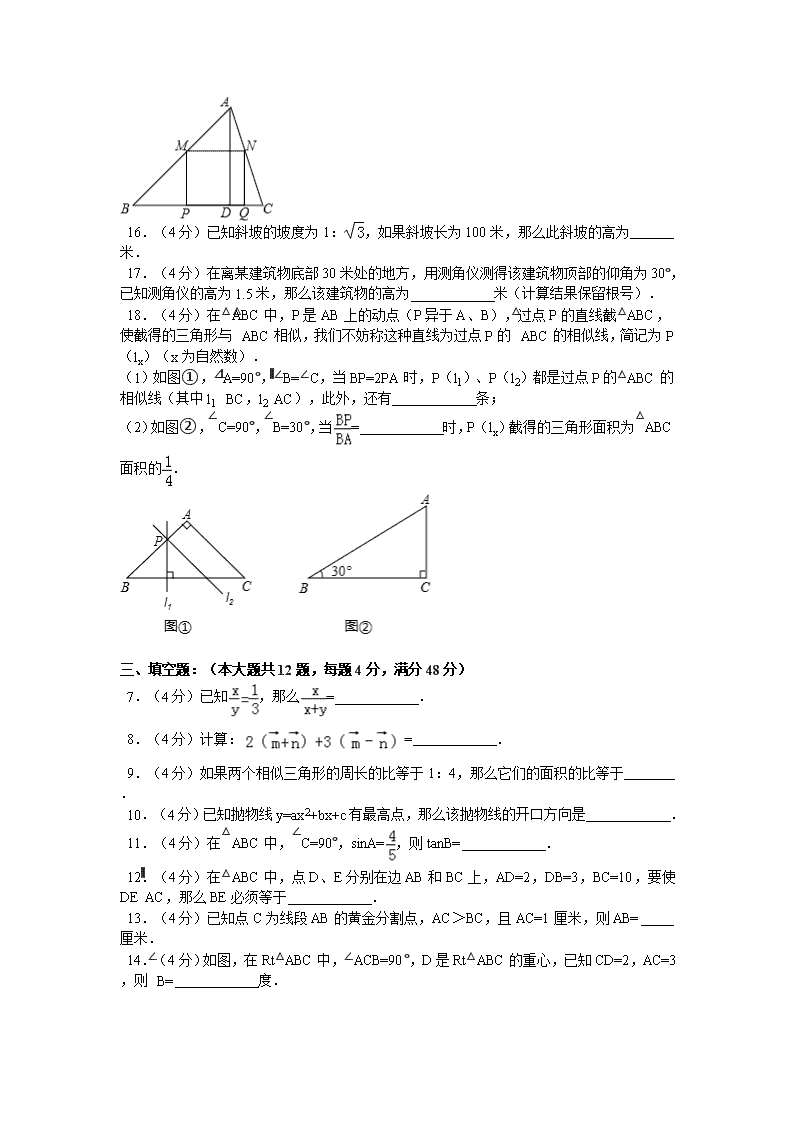
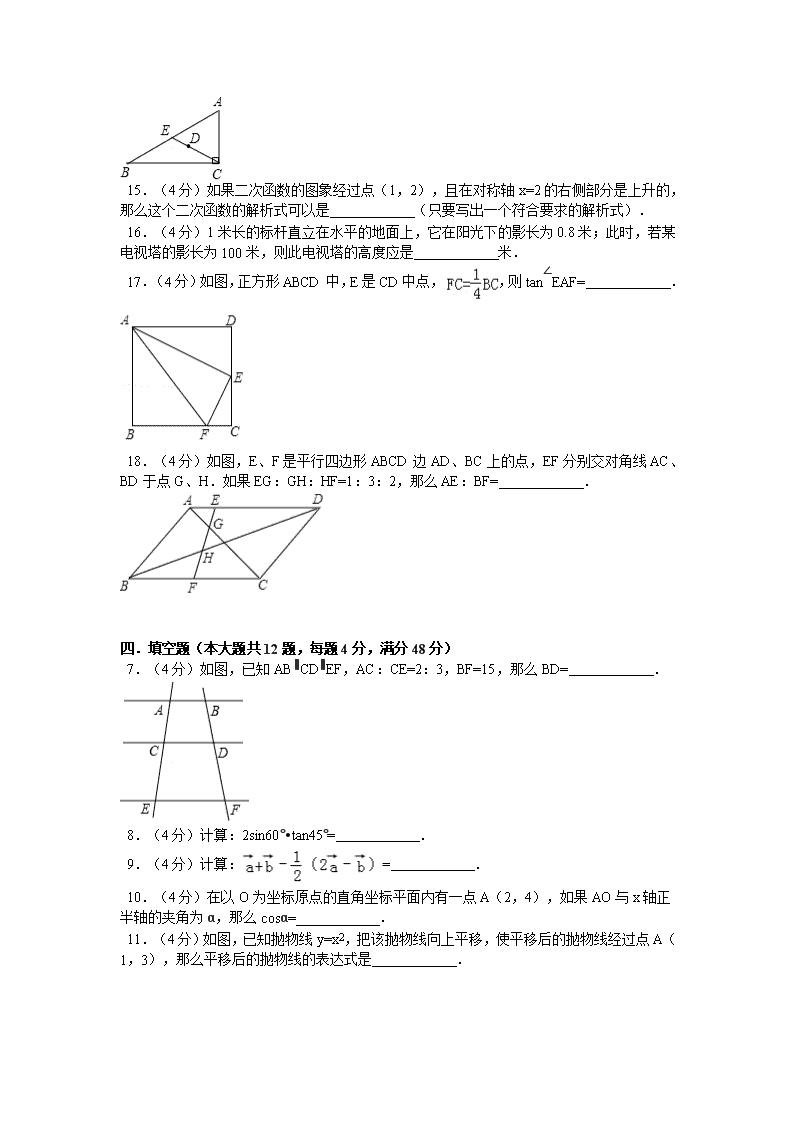
2014-2015学年上海市初三期末模拟测试卷 考试时,每套30分钟,至多35分钟 二、填空题:(本大题共12题,每题4分,满分48分) 7.(4分)若,则= . 8.(4分)若向量与单位向量的方向相反,且,则= .(用表示) 9.(4分)在△ABC中,∠C=90°,AC=3,AB=5,则cosB= . 10.(4分)已知α为锐角,且,则sinα= . 11.(4分)已知抛物线y=x2﹣2x﹣3,它的图象在对称轴 的部分是下降的. 12.(4分)如图,在平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果,那么= . 13.(4分)如图,如果l1∥l2∥l3,AC=12,DE=3,EF=5,那么BC= . 14.(4分)如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC= . 15.(4分)如图,四边形PMNQ是正方形,△ABC的高AD=6cm,BC=12cm,则正方形PMNQ的边长是 cm. 16.(4分)已知斜坡的坡度为1:,如果斜坡长为100米,那么此斜坡的高为 米. 17.(4分)在离某建筑物底部30米处的地方,用测角仪测得该建筑物顶部的仰角为30°,已知测角仪的高为1.5米,那么该建筑物的高为 米(计算结果保留根号). 18.(4分)在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线,简记为P(lx)(x为自然数). (1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(l1)、P(l2)都是过点P的△ABC的相似线(其中l1⊥BC,l2∥AC),此外,还有 条; (2)如图②,∠C=90°,∠B=30°,当= 时,P(lx)截得的三角形面积为△ABC面积的. 三、填空题:(本大题共12题,每题4分,满分48分) 7.(4分)已知,那么= . 8.(4分)计算:= . 9.(4分)如果两个相似三角形的周长的比等于1:4,那么它们的面积的比等于 . 10.(4分)已知抛物线y=ax2+bx+c有最高点,那么该抛物线的开口方向是 . 11.(4分)在△ABC中,∠C=90°,sinA=,则tanB= . 12.(4分)在△ABC中,点D、E分别在边AB和BC上,AD=2,DB=3,BC=10,要使DE∥AC,那么BE必须等于 . 13.(4分)已知点C为线段AB的黄金分割点,AC>BC,且AC=1厘米,则AB= 厘米. 14.(4分)如图,在Rt△ABC中,∠ACB=90°,D是Rt△ABC的重心,已知CD=2,AC=3,则∠B= 度. 15.(4分)如果二次函数的图象经过点(1,2),且在对称轴x=2的右侧部分是上升的,那么这个二次函数的解析式可以是 (只要写出一个符合要求的解析式). 16.(4分)1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米;此时,若某电视塔的影长为100米,则此电视塔的高度应是 米. 17.(4分)如图,正方形ABCD中,E是CD中点,,则tan∠EAF= . 18.(4分)如图,E、F是平行四边形ABCD边AD、BC上的点,EF分别交对角线AC、BD于点G、H.如果EG:GH:HF=1:3:2,那么AE:BF= . 四.填空题(本大题共12题,每题4分,满分48分) 7.(4分)如图,已知AB∥CD∥EF,AC:CE=2:3,BF=15,那么BD= . 8.(4分)计算:2sin60°•tan45°= . 9.(4分)计算:= . 10.(4分)在以O为坐标原点的直角坐标平面内有一点A(2,4),如果AO与x轴正半轴的夹角为α,那么cosα= . 11.(4分)如图,已知抛物线y=x2,把该抛物线向上平移,使平移后的抛物线经过点A(1,3),那么平移后的抛物线的表达式是 . 12.(4分)二次函数y=(m+1)x2+4x﹣m2+1的图象过原点,则m . 13.(4分)抛物线y=ax2+bx+c过(﹣1,0)和(5,0)两点,那么该抛物线的对称轴是 . 14.(4分)已知函数y=﹣2x2﹣5x+3,当x 时,y随x增大而增大. 15.(4分)一小球沿坡度为1:2.4的斜坡由高向下滚动,若小球在斜坡滚过26米,则这小球下降的了 米. 16.(4分)九年级数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列出了如下的表格: x … 0 1 2 3 4 … y=ax2+bx+c … 3 0 ﹣1 0 3 … 那么该二次函数在x=5时,y= . 17.(4分)如图,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC,那么CD= . 18.(4分)如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F⊥CD时,的值为 . 五、填空题(本大题共12题,每题4分,满分48分) 7.(4分)已知两个相似三角形的面积比是4:1,则这两个三角形的周长比是 . 8.(4分)如图,直线a∥b∥c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,已知AC=4,CE=6,BD=3,则BF等于 . 9.(4分)将二次函数y=2x2﹣4x配方成y=a(x+m)2+k的形式,配方后的解析式为 . 10.(4分)如图,王大伯屋后有一块长12米,宽8米的矩形空地ABCD,他在以较长边BC为直径的半圆形内中菜,他家养的羊平时栓在A处的一棵树上,为了不让羊吃到菜,栓羊的绳长应小于 . 11.(4分)已知抛物线y=mx2+4x+m(m﹣2)经过坐标原点,则实数m的值是 . 12.(4分)已知抛物线y=2x2+bx+c经过点A(0,3)、B(4,3),则此抛物线的对称轴是 . 13.(4分)已知⊙A的半径为5,圆心A(3,4),坐标原点O与⊙A的位置关系是 . 14.(4分)印刷厂10月份印刷一畅销小说5万册,因购买此书人数激增,印刷厂需加印,若设印书量每月的增长率为x,12月印书数量y万册,写出y关于x的函数解析式 . 15.(4分)在Rt△ABC中,∠C=90°,中线AF和中线BE交于点G,若AB=3,则CG= . 16.(4分)某小山坡的坡长为200米,山坡的高度为100米,则该山坡的坡度i= . 17.(4分)已知点A(0,y1)、B(1,y2)、C(3,y3)在抛物线y=ax2﹣2ax+1(a<0)上,则y1、y2、y3的大小关系是 (用“<”联结). 18.(4分)如图,已知△ABC是面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).查看更多