- 2021-05-25 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考卷 普通高等学校招生考试北京理科数学
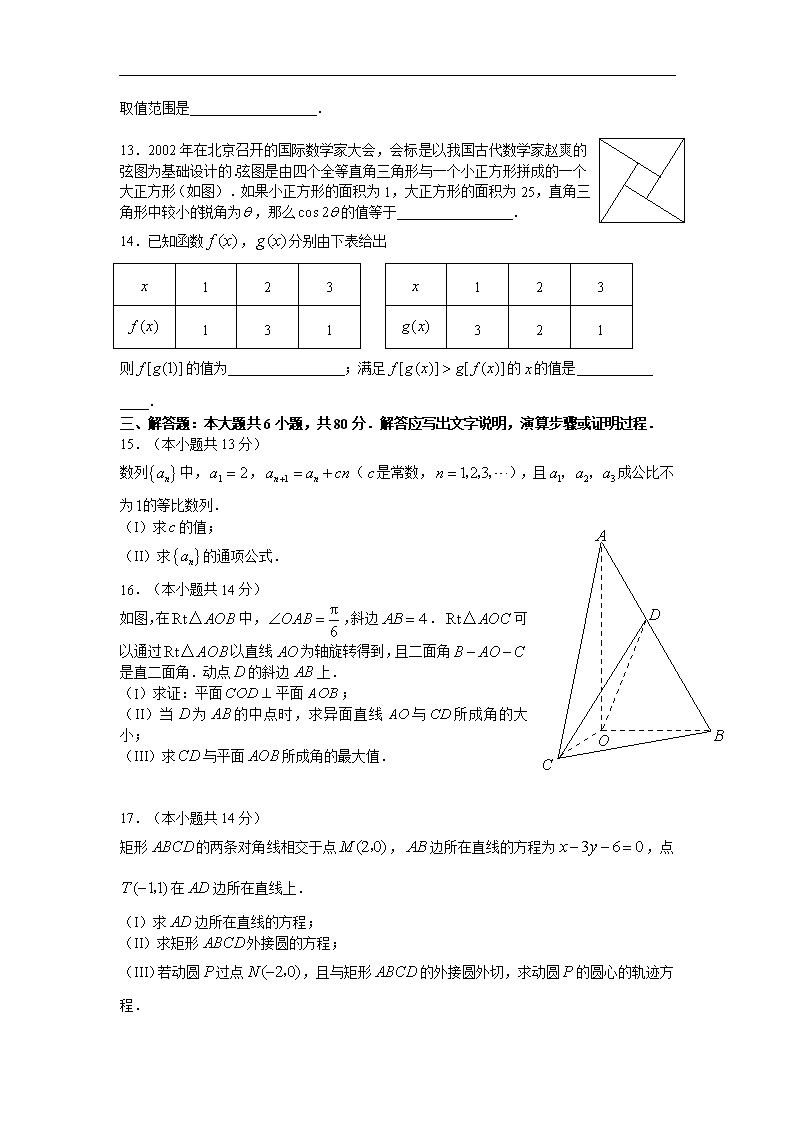
2007年普通高等学校招生全国统一考试 数学(理工农医类)(北京卷) 本试卷分第 I卷(选择题)和第 II(非选择题)两部分,第 I 卷 1 至 2 页,第 II 卷 3 至 9页,共 150分.考试时间 120分钟.考试结束,将本试卷和答题卡一并交回. 第 I卷(选择题 共 40分) 注意事项: 1.答第 I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上. 2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡 皮擦干净后,再选涂其他答案.不能答在试卷上. 一、本大题共 8小题,每小题 5分,共 40分.在每小题列出的四个选项中,选出符合题目 要求的一项. 1.已知 cos tan 0 ,那么角 是( ) A.第一或第二象限角 B.第二或第三象限角 C.第三或第四象限角 D.第一或第四象限角 2.函数 ( ) 3 (0 2)xf x x ≤ 的反函数的定义域为( ) A. (0 ), B. (1 9], C. (0 1), D.[9 ), 3.平面∥平面 的一个充分条件是( ) A.存在一条直线 a a , ∥ , ∥ B.存在一条直线 a a a , , ∥ C.存在两条平行直线 a b a b a b , , , , ∥ , ∥ D.存在两条异面直线 a b a a b , , , ∥ , ∥ 4.已知O是 ABC△ 所在平面内一点,D为 BC边中点,且 2OA OB OC 0 ,那么 ( ) A. AO OD B. 2AO OD C. 3AO OD D. 2AO OD 5.记者要为 5名志愿者和他们帮助的 2 位老人拍照,要求排成一排,2 位老人相邻但不排 在两端,不同的排法共有( ) A.1440种 B.960种 C.720种 D.480种 6.若不等式组 2 2 0 x y x y y x y a ≥ , ≤ , ≥ , ≤ 表示的平面区域是一个三角形,则 a的取值范围是( ) A. 4 3 a≥ B.0 1a ≤ C. 41 3 a≤ ≤ D.0 1a ≤ 或 4 3 a≥ 7.如果正数a b c d, , , 满足 4a b cd ,那么( ) A. ab c d≤ ,且等号成立时 a b c d, , , 的取值唯一 B. ab c d≥ ,且等号成立时 a b c d, , , 的取值唯一 C. ab c d≤ ,且等号成立时 a b c d, , , 的取值不唯一 D. ab c d≥ ,且等号成立时 a b c d, , , 的取值不唯一 8.对于函数① ( ) lg( 2 1)f x x ,② 2( ) ( 2)f x x ,③ ( ) cos( 2)f x x ,判断如下 三个命题的真假: 命题甲: ( 2)f x 是偶函数; 命题乙: ( )f x 在 ( ) , 上是减函数,在 (2 ), 上是增函数; 命题丙: ( 2) ( )f x f x 在 ( ) , 上是增函数. 能使命题甲、乙、丙均为真的所有函数的序号是( ) A.①③ B.①② C.③ D.② 2007年普通高等学校招生全国统一考试 数学(理工农医类)(北京卷) 第 II卷(共 110分) 注意事项: 1.用钢笔或圆珠笔将答案直接写在试卷上. 2.答卷前将密封线内的项目填写清楚. 二、填空题:本大题共 6小题,每小题 5分,共 30分.把答案填在题中横线上. 9. 2 2 (1 )i . 10.若数列 na 的前 n项和 2 10 ( 1 2 3 )nS n n n ,,, ,则此数列的通项公式为 ;数列 nna 中数值最小的项是第 项. 11.在 ABC△ 中,若 1tan 3 A , 150C , 1BC ,则 AB . 12.已知集合 | 1A x x a ≤ , 2 5 4 0B x x x ≥ .若 A B ,则实数 a的 取值范围是 . 13.2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的 弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一 个大正方形(如图).如果小正方形的面积为 1,大正方形的面积为 25,直 角三角形中较小的锐角为 ,那么 cos 2 的值等于 . 14.已知函数 ( )f x , ( )g x 分别由下表给出 则 [ (1)]f g 的值为 ;满足 [ ( )] [ ( )]f g x g f x 的 x的值是 . 三、解答题:本大题共 6小题,共 80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共 13分) 数列 na 中, 1 2a , 1n na a cn ( c是常数, 1 2 3n ,,, ),且 1 2 3a a a, , 成公比不 为1的等比数列. (I)求 c的值; (II)求 na 的通项公式. 16.(本小题共 14分) 如图,在Rt AOB△ 中, π 6 OAB ,斜边 4AB .Rt AOC△ 可 以通过Rt AOB△ 以直线 AO为轴旋转得到,且二面角 B AO C 是直二面角.动点D的斜边 AB上. (I)求证:平面COD 平面 AOB; (II)当D为 AB的中点时,求异面直线 AO与CD所成角的大小; (III)求CD与平面 AOB所成角的最大值. 17.(本小题共 14分) 矩形 ABCD的两条对角线相交于点 (2 0)M , , AB边所在直线的方程为 3 6 0x y ,点 ( 11)T ,在 AD边所在直线上. (I)求 AD边所在直线的方程; (II)求矩形 ABCD外接圆的方程; (III)若动圆 P过点 ( 2 0)N , ,且与矩形 ABCD的外接圆外切,求动圆 P的圆心的轨迹方 程. x 1 2 3 ( )f x 1 3 1 x 1 2 3 ( )g x 3 2 1 O C A D B 18.(本小题共 13分) 某中学号召学生在今年春节期间至少参加一次社会 公益活动(以下简称活动).该校合唱团共有 100 名学生,他们参加活动的次数统计如图所示. (I)求合唱团学生参加活动的人均次数; (II)从合唱团中任意选两名学生,求他们参加活 动次数恰好相等的概率. (III)从合唱团中任选两名学生,用 表示这两人 参加活动次数之差的绝对值,求随机变量 的分布 列及数学期望 E . 19.(本小题共 13分) 如图,有一块半椭圆形钢板,其半轴长为 2r,短半轴长为 r,计划将此钢板切割成等腰梯 形的形状,下底 AB是半椭圆的短轴,上底CD的端点在椭圆上,记 2CD x ,梯形面积 为 S. (I)求面积 S以 x为自变量的函数式,并写出其定义域; (II)求面积 S的最大值. 20.已知集合 1 2 ( 2)kA a a a k , , , ≥ ,其中 ( 1 2 )ia i k Z ,, , ,由 A中的元素构 成两个相应的集合: ( )S a b a A b A a b A , , , , ( )T a b a A b A a b A , , , . 其中 ( )a b, 是有序数对,集合 S和T 中的元素个数分别为m和 n. 若对于任意的 a A ,总有 a A ,则称集合 A具有性质 P. (I)检验集合 01 2 3,,, 与 1 2 3 ,, 是否具有性质P并对其中具有性质P的集合,写出相应 的集合 S和T ; (II)对任何具有性质 P的集合 A,证明: ( 1) 2 k kn ≤ ; (III)判断m和 n的大小关系,并证明你的结论. 1 2 3 10 20 30 40 50 参加人数 活动次数 4r CD A B2r 2007年普通高等学校招生全国统一考试 数学(理工农医类)(北京卷)答案 一、选择题(本大题共 8小题,每小题 5分,共 40分) 题号 1 2 3 4 5 6 7 8 答案 C B D A B D A D 1.∵ cos tan 0 ,∴ 当 cosθ<0,tanθ>0 时,θ∈第三象限;当 cosθ>0,tanθ<0时,θ ∈第四象限,选 C。 2.函数 ( ) 3 (0 2)xf x x ≤ 的反函数的定义域为原函数的值域,原函数的值域为 (1 9], , ∴ 选 B。 3 . 平 面 ∥ 平 面 的 一 个 充 分 条 件 是 “ 存 在 两 条 异 面 直 线 a b a a b , , , ∥ , ∥ ”,选 D。 4. O 是 ABC△ 所在平面内一点, D 为 BC 边中点,∴ 2OB OC OD ,且 2OA OB OC 0 ,∴ 2 2 0OA OD ,即 AO OD ,选 A 5. 5名志愿者先排成一排,有 5 5A 种方法,2位老人作一组插入其中,且两位老人有左右顺 序,共有 5 52 4 A =960种不同的排法,选 B。 6.不等式组 2 2 0 x y x y y x y a ≥ , ≤ , ≥ , ≤ ,将前三个不等式画出可行域,三 个顶点分别为(0,0),(1,0),( 3 2 , 3 2 ),第四个不等式 x y a , 表示的是斜率为-1的直线的下方,∴ 当 0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档