江苏高考立体几何典型题学生

江苏高考立体几何典型题学生

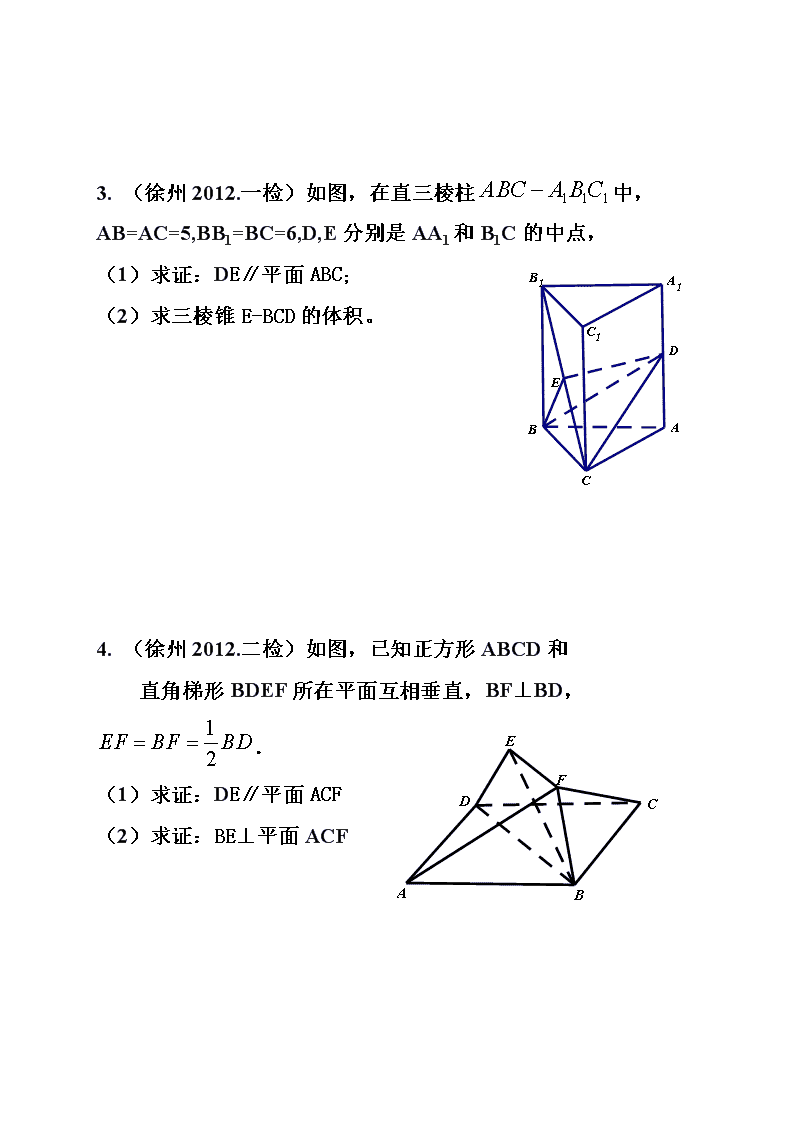
‎ 江苏高考数学例题几何题型解析 ‎1．(徐州2013.二检)如图，在三棱柱中，‎ 已知，，分别为棱，，的中点，‎ ‎，平面，，为垂足．‎ 求证：（1）平面；‎ ‎（2）平面．‎ ‎2．（徐州2012年考前信息卷）如图，四棱锥的 底面是边长为的正方形，平面，点是的中点．‎ ‎⑴求证：平面；‎ ‎⑵求证：平面平面；‎ ‎⑶若，求三棱锥的体积．‎ ‎3. （徐州2012.一检）如图，在直三棱柱中，AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点，‎ ‎（1）求证：DE∥平面ABC；‎ ‎（2）求三棱锥E-BCD的体积。‎ ‎4. （徐州2012.二检）如图，已知正方形ABCD和 ‎ 直角梯形BDEF所在平面互相垂直，BF⊥BD， ．‎ ‎（1）求证：DE∥平面ACF ‎（2）求证：BE⊥平面ACF ‎　　　　　‎ ‎5.（徐州2011.一检）如图，在四棱锥中，‎ B A D C F E ‎ 底面为矩形，平面⊥平面，,,为的中点，‎ 求证：（1）∥平面；‎ ‎ （2）平面平面．‎ ‎6(徐州2011.三检)在直角梯形ABCD中，AB∥CD,‎ AB=2BC=4，CD=3，E为AB中点，过E作EF⊥CD,垂足为F,‎ 如（图一），将此梯形沿EF折成二面角A-EF-C,如（图二），‎ ‎（1）求证BF∥平面ACD;‎ ‎(2)求多面体ADFCBE的体积。‎ ‎7(宿迁2013.三检). 如图，，均为圆的直径，‎ 圆所在的平面，.‎ 求证：⑴平面平面； ‎ ‎ ⑵直线DF∥平面．‎ ‎8(宿迁2013.二检).如图，四边形ABCD是正方形，‎ PB^平面ABCD，MA^平面ABCD，PB＝AB＝2MA.‎ 求证：（1）平面AMD∥平面BPC； ‎ ‎ （2）平面PMD^平面PBD．‎ ‎9(苏锡常镇四市2012二检)如图，在三棱锥中，‎ 平面分别与，，，交于点，，，，‎ 且平面，，‎ 求证：（1）平面；‎ ‎ （2）；‎ ‎ （3）平面.‎ ‎10.（2010江苏）如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。‎ ‎（1）求证：PC⊥BC； （2）求点A到平面PBC的距离。‎ ‎ ‎ ‎11．（2011江苏）如图，在四棱锥中，‎ 平面平面，，，‎ 分别是的中点．‎ 求证：（1）直线平面；‎ ‎（2）平面平面．‎ ‎12．（2012江苏）如图，在直三棱柱中，，分别是棱上的点（点 不同于点），且为的中点．‎ 求证：（1）平面平面；（2）直线平面．‎ ‎13.（2013江苏）如图，在三棱锥中，平面平面，，，过作，垂足为，点分别是棱的中点．求证：‎