- 2021-05-24 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
广东省广州市荔湾区2020-2021学年第一学期八年级期末考试数学试卷 Word版无答案
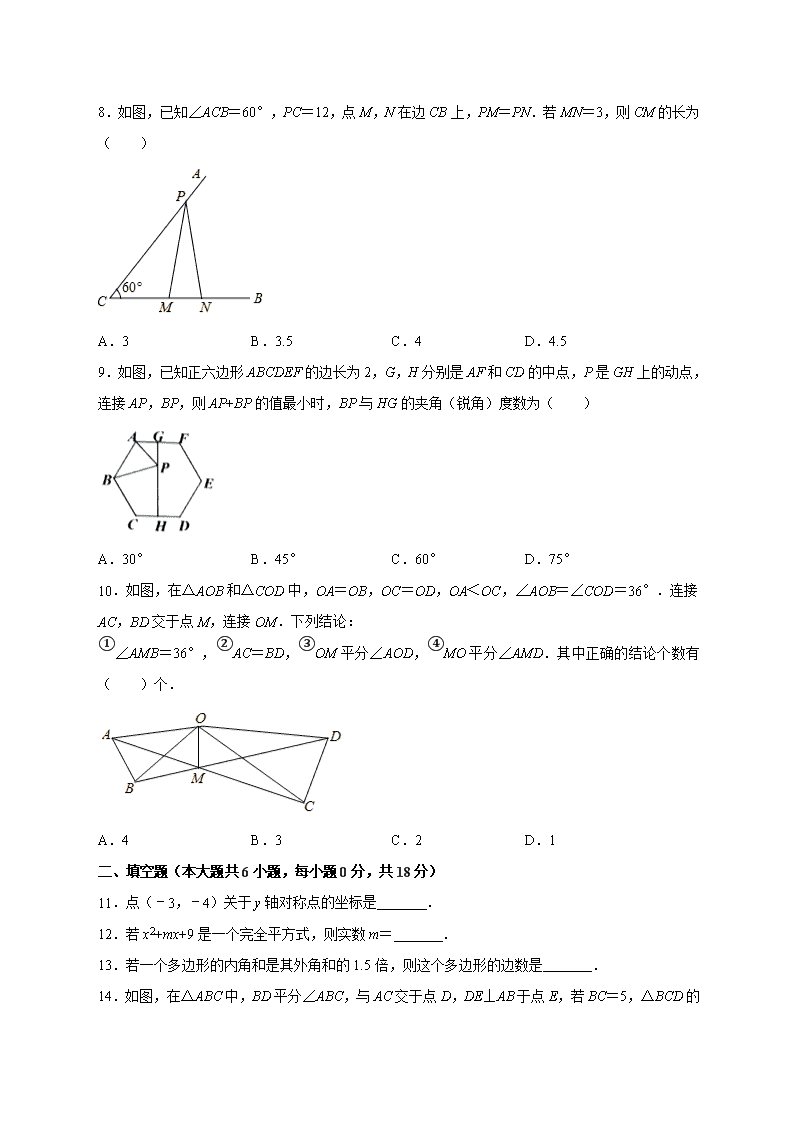
2020-2021 学年广东省广州市荔湾区八年级(上)期末数学试卷 一、选择题(本大题共 10 小题,每小题 3 分,共 30 分,在每小题给出的四个选项中,只有一项符 合题目要求的.) 1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( ) A. 赵爽弦图 B. 笛卡尔心形线 C. 科克曲线 D. 斐波那契螺旋线 2.要使分式 有意义,x 应满足的条件是( ) A.x>3 B.x<3 C.x≠﹣3 D.x≠3 3.下列运算正确的是( ) A.a4•a2=a8 B.a6÷a2=a3 C.(2ab2)2=4a2b⁴ D.(a3)2=a5 4.如果把 中的 x 和 y 都扩大 5 倍,那么分式的值( ) A.扩大 5 倍 B.不变 C.缩小为原来的 D.扩大 4 倍 5.长度为 2cm、3cm、4cm、5cm 的 4 条线段,若以其中的三条线段为边构成三角形,可以构成不 同的三角形共有( ) A.1 个 B.2 个 C.3 个 D.4 个 6.如果将一副三角板按如图方式叠放,那么∠1 等于( ) A.120° B.105° C.60° D.45° 7.若 2x+m 与 x+3 的乘积中不含 x 的一次项,则 m 的值为( ) A.﹣6 B.0 C.﹣2 D.3 8.如图,已知∠ACB=60°,PC=12,点 M,N 在边 CB 上,PM=PN.若 MN=3,则 CM 的长为 ( ) A.3 B.3.5 C.4 D.4.5 9.如图,已知正六边形 ABCDEF 的边长为 2,G,H 分别是 AF 和 CD 的中点,P 是 GH 上的动点, 连接 AP,BP,则 AP+BP 的值最小时,BP 与 HG 的夹角(锐角)度数为( ) A.30° B.45° C.60° D.75° 10.如图,在△AOB 和△COD 中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接 AC,BD 交于点 M,连接 OM.下列结论: ① ∠AMB=36°, ② AC=BD, ③ OM 平分∠AOD, ④ MO 平分∠AMD.其中正确的结论个数有 ( )个. A.4 B.3 C.2 D.1 二、填空题(本大题共 6 小题,每小题 0 分,共 18 分) 11.点(﹣3,﹣4)关于 y 轴对称点的坐标是 . 12.若 x2+mx+9 是一个完全平方式,则实数 m= . 13.若一个多边形的内角和是其外角和的 1.5 倍,则这个多边形的边数是 . 14.如图,在△ABC 中,BD 平分∠ABC,与 AC 交于点 D,DE⊥AB 于点 E,若 BC=5,△BCD 的 面积为 5,则 ED 的长为 . 15.关于 x 的分式方程 + =1 有增根,则 m 的值为 . 16.如图,在△ABC 中,AF 平分∠BAC,AC 的垂直平分线交 BC 于点 E,∠B=60°,∠FAE=21 °,则∠C= 度. 三、解答题(本大题共 9 题,共 72 分,解答应写出文字说明、证明过程或演算步骤.) 17.计算:(x﹣1)(x+1)﹣(x+2)2. 18.分解因式:a2(a﹣b)+25(b﹣a). 19.计算:(1) ﹣ ;(2)( +a)÷ . 20.解方程: ﹣ =1. 21.已知:如图,锐角△ABC 的两条高 BD、CE 相交于点 O,且 OB=OC. (1)求证:BE=CD;(2)判断点 O 是否在∠BAC 的角平分线上,并说明理由. 22.如图,△ABC 三个顶点的坐标分别为 A(1,1)、B(4,2)、C(3,5). (1)若△A'B'C'与△ABC 关于 x 轴成轴对称,作出△A'B'C'; (2)若 P 为 y 轴上一点,使得△APC 周长最小,在图中作出点 P,并写出 P 点的坐标为 ; (3)计算△ABC 的面积. 23.某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的 2.5 倍,用 800 元单独购买甲图书比用 800 元单独购买乙图书要少 24 本. (1)甲、乙两种图书每本价格分别为多少元? (2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的 2 倍多 8 本,且用于购买甲、乙两种 图书的总经费不超过 1060 元,那么该图书馆最多可以购买多少本乙图书? 24.已知△ABC 中,AC=BC,点 D 是边 AB 上一点,点 P 为 BC 边上一点.(1)如图 1,若∠ACB =90°,连接 CD,以 CD 为一边作等腰直角△DCE,∠DCE=90°,连接 BE,求证:BE=AD.(2) 如图 2,若∠ACB=90°,以 PD 为一边作等腰直角△PDE,∠DPE=90°,连接 BE,求∠EBD 的 度数.(3)如图 3,若把(1)中的条件改为:∠ACB=60°,以 PD 为一边作等边△PDE,连接 BE.求 ∠EBD 的度数. 25.如图,△ABC 为等边三角形,点 D、E 分别是边 AB、BC 所在直线上的动点,若点 D、E 以相 同的速度,同时从点 A、点 B 出发,分别延 AB、BC 方向运动,直线 AE、CD 交于点 O. (1)如图 1,求证:△ABE≌△CAD; (2)在点 D、点 E 运动过程中,∠COE= °; (3)如图 2,点 P 为边 AC 中点,连接 BO,PO,当点 D、E 分别在线段 AB、BC 上运动时,判断 BO 与 PO 的数量关系,并证明你的结论.查看更多