八年级数学上册第13章全等三角形专题课堂三课件新版华东师大版

八年级数学上册第13章全等三角形专题课堂三课件新版华东师大版

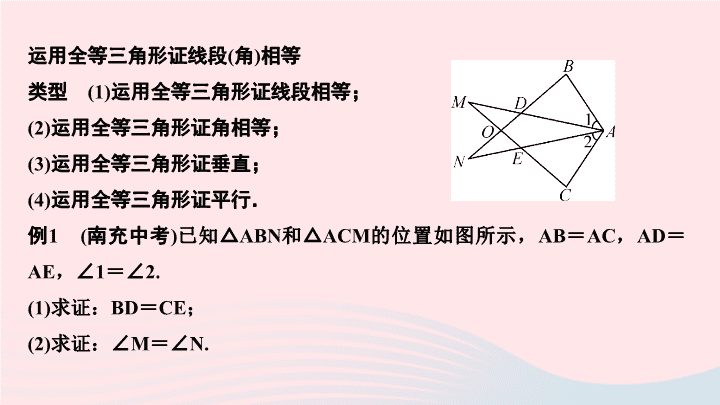
第13章　全等三角形 专题课堂(三)　全等三角形 运用全等三角形证线段 ( 角 ) 相等 类型　 (1) 运用全等三角形证线段相等； ( 2) 运用全等三角形证角相等； (3) 运用全等三角形证垂直； (4) 运用全等三角形证平行． 例 1 　 ( 南充中考 ) 已知△ ABN 和△ ACM 的位置如图所示， AB ＝ AC ， AD ＝ AE ，∠ 1 ＝∠ 2. (1) 求证： BD ＝ CE ； (2) 求证：∠ M ＝∠ N. 分析： (1) 由 S . A . S . 证明 △ ABD ≌△ ACE ， 得出对应边相等即可； ( 2) 证出 ∠ BAN ＝ ∠ CAM ， 由全等三角形的性质得出 ∠ B ＝ ∠ C ， 由 A . A . S . 证明 △ ACM ≌△ ABN ， 得出对应角相等即可． 【 对应训练 】 1 ． ( 黄冈中考 ) 已知：如图，∠ BAC ＝∠ DAM ， AB ＝ AN ， AD ＝ AM ，求证：∠ B ＝∠ ANM. 2 ． ( 武汉中考 ) 如图，点 C ， F ， E ， B 在一条直线上，∠ CFD ＝∠ BEA ， CE ＝ BF ， DF ＝ AE ，写出 CD 与 AB 之间的关系，并证明你的结论． 中线倍长法 类型　 (1) 已知三角形的中线 ，利用中线倍长法， 求中线的取值范围； (2) 已知线段的中点 ， 利用中线倍长法 ， 以中点为公共顶点构造全等三角形． 例 2 　如图， AD 为△ ABC 的中线，求证： AB ＋ AC ＞ 2AD. 证明：延长 AD 至点 M ，使 DM ＝ AD ，连结 BM ，在△ ADC 和△ MDB 中， CD ＝ BD ，∠ ADC ＝∠ MDB ， AD ＝ MD ，∴△ ADC≌△MDB( S . A . S .) ，∴ BM ＝ AC.∵ 在△ ABM 中， AB ＋ BM ＞ AM ，∴ AB ＋ AC ＞ 2AD 分析： 延长 AD 至点 M ， 使 DM ＝ AD ， 连结 BM ， 易证 △ ADC ≌△ MDB ， 得 BM ＝ AC ， 在 △ ABM 中 ， AB ＋ BM ＞ AM ， 即 AB ＋ AC ＞ 2AD. 【 对应训练 】 3 ．在△ ABC 中， AB ＝ 5 ， AC ＝ 3 ，则中线 AD 的取值范围为 ______________ ． 1 ＜ AD ＜ 4 截长补短法证线段和差问题 类型　 (1) 截长法； (2) 补短法． 例 3 　 如图，已知 AD∥BC ，∠ ABC 和∠ BAD 的平分线相交于点 E ，过点 E 的直线分别交 AD ， BC 于点 D ， C. 求证： AB ＝ AD ＋ BC. 证明：在 AB 上截取 AM ＝ AD ，连结 EM ，∵ AE ， BE 分别平分∠ BAD 和∠ ABC ，∴∠ MAE ＝∠ DAE ，∠ MBE ＝∠ CBE. 在△ AME 和△ ADE 中，∵ AM ＝ AD ，∠ MAE ＝∠ DAE ， AE ＝ AE ，∴△ AME≌△ADE( S . A . S .) ，∴∠ AME ＝∠ D.∵AD∥BC ，∴∠ C ＋∠ D ＝ 180°.∵∠BME ＋∠ AME ＝ 180° ，∴∠ C ＝∠ BME. 又∵ BE ＝ BE ，∠ MBE ＝∠ CBE ，∴△ BME≌△BCE( A . A . S .) ，∴ BC ＝ BM.∵AB ＝ AM ＋ BM ，∴ AB ＝ AD ＋ BC 分析： 在 AB 上截取 AM ＝ AD ， 连结 EM ， 可得 △ AME ≌△ ADE ， 再想办法证 △ BME ≌△ BCE ， 得 BC ＝ BM ， 即得 AB ＝ AM ＋ BM ＝ AD ＋ BC. 【 对应训练 】 4 ．如图，在△ ABC 中，∠ B ＝ 60° ，∠ BAC 与∠ BCA 的平分线 AD ， CE 分别交 BC 和 AB 于点 D ， E ， AD 与 CE 相交于点 F. 求证： AC ＝ AE ＋ CD. 5 ．已知，在四边形 ABCD 中，∠ A ＝∠ C ＝ 90° ，∠ D ＝ 60° ， AB ＝ BC. (1) 如图①，若 E ， F 分别在线段 AD ， CD 上，且∠ EBF ＝ 60°. 求证： EF ＝ AE ＋ CF ； (2) 如图②，若 E ， F 分别在线段 AD ， DC 的延长线上，且∠ EBF ＝ 60° ，求证： EF ＝ AE － CF. 解：∠ ABC ＝ 360° －∠ A －∠ C －∠ D ＝ 120° ， (1) 延长 EA 至点 M ，使 AM ＝ CF ，连结 BM ，易证△ ABM≌△CBF( S . A . S .) ，∴ BM ＝ BF ，∠ ABM ＝∠ CBF ，∴∠ EBM ＝∠ ABE ＋∠ ABM ＝∠ ABE ＋∠ CBF ＝∠ ABC －∠ EBF ＝ 120° － 60° ＝ 60° ＝∠ EBF ，易证△ BEM≌△BEF( S . A . S .) ，∴ EF ＝ EM ＝ AE ＋ AM ＝ AE ＋ CF 　 (2) 在 AE 上截取 AN ＝ CF ，连结 BN ，易证△ ABN≌△CBF( S . A . S .) ，∴ BN ＝ BF ，∠ ABN ＝∠ CBF ，∴∠ EBN ＝∠ ABC － (∠EBC ＋∠ ABN) ＝∠ ABC － (∠EBC ＋∠ CBF) ＝∠ ABC －∠ EBF ＝ 120° － 60° ＝ 60° ＝∠ EBF ，易证△ BEN≌△BEF( S . A . S .) ，∴ EF ＝ EN ＝ AE － AN ＝ AE － CF