八年级下数学课件八年级下册数学课件《等腰三角形》 北师大版 (7)_北师大版

八年级下数学课件八年级下册数学课件《等腰三角形》 北师大版 (7)_北师大版

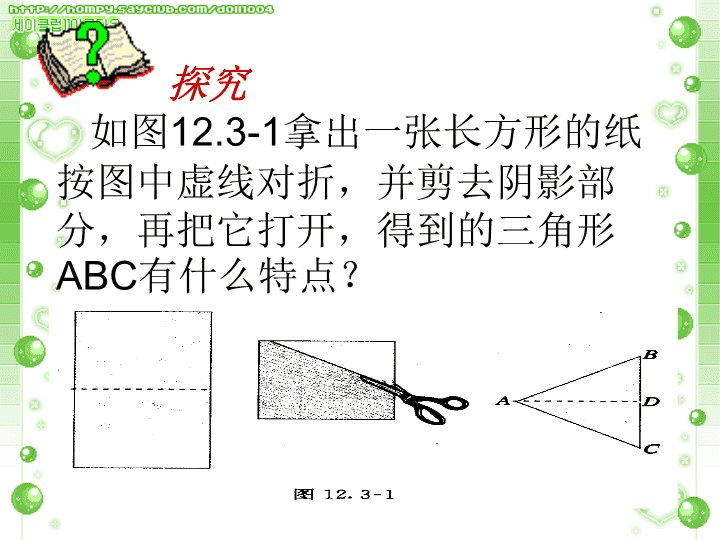
学习目标 1、了解等腰三角形的有关概念。 2、掌握识别等腰三角形的两种方 法。 3、掌握并能熟练应用等腰三角形 的性质定理和三线合一性质解决有 关问题。 4、通过习题，能总结代数法求几 何角的大小、线段长度的方法。 探究 如图12.3-1拿出一张长方形的纸 按图中虚线对折，并剪去阴影部 分，再把它打开，得到的三角形 ABC有什么特点？ 定义：我们知道两条边相等的三角形叫 做等腰三角形（isosceles triangle）.如图 所示，AB＝AC，△ABC就是等腰三角形. 等腰三角形中， 相等的两边都叫腰， 另一边叫做底边， 两腰的夹角叫做角， 腰和底边的夹角叫底角. 想一想 1、上面剪出的等腰三角形是轴对称图形吗？ 2、把剪出的等腰三角形ABC沿折痕对折，找出 其中重合的线段和角。 3、由这些重合的线段和角，你能发现等腰三角 形的哪些性质呢？说一说你的猜想。 我们可以发现等腰三角形的性质 性质1：等腰三角形的两个底角相等（简写为 “等边对等角”） 性质2：等腰三角形的顶角平分线、底边上的中 线、底边上的高线相互重合（简称为“三线合 一”） 证明性质1:等腰三角形的两个底角相 等 已知： △ ABC中， AB=AC. 求证： ∠B= ∠C. A B C 21 作顶角的平分线 证明：作顶角的平分线AD. 在△BAD和△CAD中， AB=AC ( 已知 ), ∠ 1= ∠ 2 ( 辅助线作法 )， AD=AD (公共边) , ∴ △BAD ≌ △CAD (SAS). ∴ ∠B= ∠C. 想一想，做一 做：我们如何 证明性质2呢？ 如图在△ABC中，AB=AC，点D在 AC上，且 BD=BC=AD求△ABC各 角的度数. 解：∵AB=AC， BD=BC=AD ∴∠ABC=∠C=∠BDC ∠A=∠ABD 设∠A=x,则 ∠BDC=∠A+∠ABD=2x° 从而∠ABC=∠C=∠BDC=2x° 于是在△ABC中，有 ∠A+∠ABC+∠C=x+2x+2x=180 解得x=36 在△ABC中，∠A=36°, ∠ABC=∠C=72°. 1 、在等腰△ABC中，AB =AC, ∠A = 36°,则∠B =——，∠C=—— 2、在等△ABC腰中，AB=AC,∠A = 50°, 则∠B =——，∠C=—— 3、在等△ABC腰中，AB=AC,∠A = 120°则 ∠B =——，∠C=—— 72° 72° 65°65° 30° 30° v1、△ ABC是等腰直角三角形（AB=AC,∠BAC=90°）， AD是底边BC上的高，标出∠ B， ∠ C， ∠ BAD， ∠ DAC 的度数，图中有哪些相等的线段？ B A C D v2、在△ ABC中，AB=AD=DC， ∠BAD=26°，求∠ B 和∠ C的度数 B D C A 这节课我们学习了什么? 1、求有关等腰三角形的问题，作 顶角平分线、底边中线，底边的 高是常用的辅助线； 2、熟练掌握求解等腰三角形的顶 角、底角的度数； 3、掌握等腰三角形三线合一的 应用。