- 2021-05-22 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学二轮复习专题四点直线平面之间的位置关系理更多关注高中学习资料库
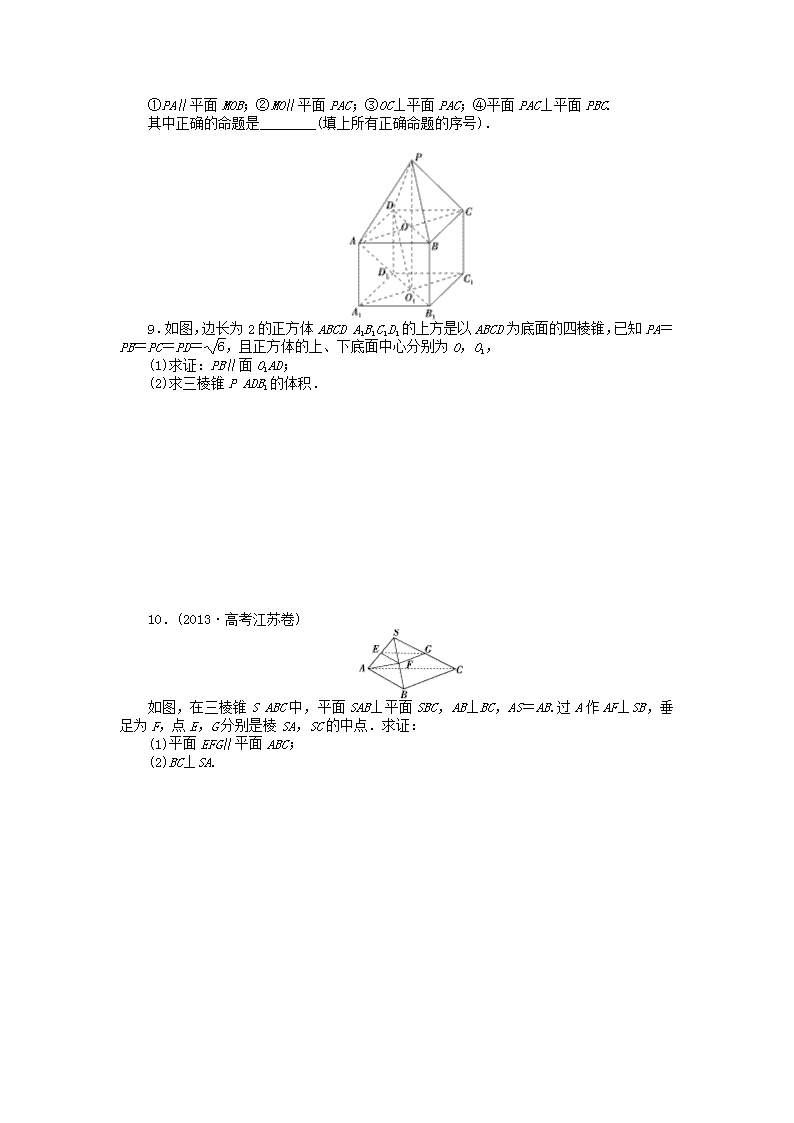
第二讲 点、直线、平面之间的位置关系 1.(2013·高考安徽卷)在下列命题中,不是公理的是( ) A.平行于同一个平面的两个平面相互平行 B.过不在同一条直线上的三点,有且只有一个平面 C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 D.如果两个不重合的平面有一个公共点, 那么它们有且只有一条过该点的公共直线 2.(2013·内蒙古乌海检测)已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( ) A.与a,b都相交 B.只能与a,b中的一条相交 C.至少与a,b中的一条相交 D.与a,b都平行 3.(2013·高考广东卷)设l为直线,α,β是两个不同的平面.下列命题中正确的是( ) A.若l∥α,l∥β,则α∥β B.若l⊥α,l⊥β,则α∥β C.若l⊥α,l∥β,则α∥β D.若α⊥β,l∥α,则l⊥β 4.(2013·河北省质量检测)已知α、β是两个不同的平面,给出下列四个条件:①存在一条直线a,a⊥α,a⊥β;②存在一个平面γ,γ⊥α,γ⊥β;③存在两条平行直线a、b,a⊂α,b⊂β,a∥β,b∥α;④存在两条异面直线a、b,a⊂α,b⊂β,a∥β,b∥α,可以推出α∥β的是( ) A.①③ B.②④ C.①④ D.②③ 5.将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2)),则在空间四面体ABCD中,AD与BC的位置关系是( ) A.相交且垂直 B.相交但不垂直 C.异面且垂直 D.异面但不垂直 6.(2013·武汉市武昌区联考)已知直线l⊥平面α,直线m⊂平面β,有下列命题: ①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β;④l⊥m⇒α∥β. 其中正确命题的序号是________. 7.(2013·广东省惠州市调研)已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的有________. ①若m∥α,n∥α,则m∥n;②若α⊥γ,β⊥γ,则α∥β; ③若m∥α,m∥β,则α∥β;④若m⊥α,n⊥α,则m∥n. 8. 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题: ①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;④平面PAC⊥平面PBC. 其中正确的命题是________(填上所有正确命题的序号). 9.如图,边长为2的正方体ABCDA1B1C1D1的上方是以ABCD为底面的四棱锥,已知PA=PB=PC=PD=,且正方体的上、下底面中心分别为O,O1, (1)求证:PB∥面O1AD; (2)求三棱锥PADB1的体积. 10.(2013·高考江苏卷) 如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证: (1)平面EFG∥平面ABC; (2)BC⊥SA. 11.如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+,过A作AE⊥CD,垂足为E,G、F分别为AD、EC的中点,现将△ADE沿AE折起,使得DE⊥EC. (1)求证:BC⊥平面CDE; (2)求证:FG∥平面BCD; (3)在线段AE上找一点R,使得平面BDR⊥平面DCB,并说明理由. 答案: 1.【解析】选A.A,不是公理,是个常用的结论,需经过推理论证; B,是平面的基本性质公理; C,是平面的基本性质公理; D,是平面的基本性质公理. 2.【解析】选C.若c与a,b都不相交,则c与a,b都平行,根据公理4,知a∥b,与a,b异面矛盾.故选C. 3.【解析】选B.选项A,若l∥α,l∥β,则α和β可能平行也可能相交,故错误; 选项B,若l⊥α,l⊥β,则α∥β,故正确; 选项C,若l⊥α,l∥β,则α⊥β,故错误; 选项D,若α⊥β,l∥α,则l与β的位置关系有三种可能:l⊥β,l∥β,l⊂β,故错误.故选B. 4.【解析】选C.对于②,平面α与β还可以相交;对于③,当a∥b时,不一定能推出α∥β,所以②③是错误的,易知①④正确,故选C. 5.【解析】选C.在题图(1)中的等腰直角三角形ABC中,斜边上的中线AD就是斜边上的高,则AD⊥BC.翻折后如题图(2),AD与BC变成异面直线,而原线段BC变成两条线段BD、CD,这两条线段与AD垂直,即AD⊥BD,AD⊥CD,BD∩CD=D,故AD⊥平面BCD,所以AD⊥BC.故选C. 6.【解析】①正确,∵l⊥α,α∥β,∴l⊥β,又m⊂β,∴l⊥m;②错误,l,m也可以垂直,还可以异面;③正确,∵l⊥α,l∥m,∴m⊥α,又m⊂β,∴α⊥β;④错误,α与β可能相交. 【答案】①③ 7.【解析】若m∥α,n∥α,m,n可以平行,可以相交,也可以异面,故①不正确;若α⊥γ,β⊥γ,α,β可以相交,故②不正确;若m∥α,m∥β,α,β可以相交,故③不正确;若m⊥α,n⊥α,则m∥n,④正确.故填④. 【答案】④ 8.【解析】①错误,PA⊂平面MOB;②正确;③错误,否则,有OC⊥AC,这与BC⊥AC矛盾;④正确,因为BC⊥平面PAC. 【答案】②④ 9. 【解】(1)如图,作OE⊥BC于E,连结PE,则PE⊥BC,易得PE==,PO=2,连接OB1得四边形PBB1O为平行四边形,于是PB∥OB1, 又OB1∥DO1, ∴PB∥DO1, 又PB⊄平面O1AD, DO1⊂平面O1AD, ∴PB∥平面O1AD. (2)由于VPADB1=VAPDB1,易得三棱锥APDB1的高即为AO=AC=, S△PDB1=SDD1B1B+S△PDB-S△DD1B1-S△PB1B =2×2+×2×2-×2×2-×2×=3, 故三棱锥PADB1的体积为VPADB1=×3×=2. 10.【证明】(1)因为AS=AB,AF⊥SB, 垂足为F,所以F是SB的中点. 又因为E是SA的中点, 所以EF∥AB. 因为EF⊄平面ABC,AB⊂平面ABC, 所以EF∥平面ABC. 同理EG∥平面ABC.又EF∩EG=E, 所以平面EFG∥平面ABC. (2)因为平面SAB⊥平面SBC,且交线为SB, 又AF⊂平面SAB,AF⊥SB,所以AF⊥平面SBC. 因为BC⊂平面SBC,所以AF⊥BC. 又因为AB⊥BC,AF∩AB=A,AF⊂平面SAB,AB⊂平面SAB,所以BC⊥平面SAB. 因为SA⊂平面SAB,所以BC⊥SA. 11.【解】(1)由已知得DE⊥AE,DE⊥EC,∵AE∩EC=E,AE、EC⊂平面ABCE,∴DE⊥平面ABCE,∴DE⊥BC.又BC⊥EC,EC∩DE=E,∴BC⊥平面CDE. (2)取AB中点H,连接GH、FH,如图所示. ∴GH∥BD,FH∥BC, ∴GH∥平面BCD,FH∥平面BCD. ∴平面FHG∥平面BCD, ∴GF∥平面BCD. (3)R点满足3AR=RE时,平面BDR⊥平面DCB.取BD中点Q,连接DR、BR、CR、CQ、RQ,如图所示: 易得CD=2,BR=,CR=,DR=,CQ=, 在△BDR中,∵BR=,DR=,BD=2,可知RQ=, ∴在△CRQ中,CQ2+RQ2=CR2,∴CQ⊥RQ. 又在△CBD中,CD=DB,Q为BD的中点, ∴CQ⊥BD,∴CQ⊥平面BDR, ∴平面BDC⊥平面BDR.查看更多