【数学】2018届一轮复习人教A版定模型求离散型随机变量的期望与方差理学案
专题71 定模型求离散型随机变量的期望与方差
考纲要求:
(1)理解取有限个值的离散型随机变量及其分布列的概念,了解分布列对于刻画随机现
象的重要性.
(2)理解超几何分布及其导出过程,并能进行简单的应用.
(3)了解条件概率和两个事件相互独立的概念,理解 n 次独立重复试验的模型及二项分
布,并能解决一些简单的实际问题.
(4)理解取有限个值的离散型随机变量均值、方差的概念,能计算简单离散型随机变量的
均值、方差,并能解决一些实际问题.
(5)利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.
基础知识回顾:
1、离散型随机变量的期望与方差.
①期望:一般地,若离散型随机变量ξ的概率分布为
…
…
P
…
…
则称为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
②方差、标准差的定义:当已知随机变量ξ的分布列为时,则称为ξ的方差. 显然,故为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.越小,稳定性越高,波动越小.
2.相互独立事件
(1)对于事件A、B,若A的发生与B的发生互不影响,则称A、B是相互独立事件.
(2)若A与B相互独立,则P(B|A)=P(B),P(AB)=P(B|A)P(A)=P(A)P(B).
(3)若A与B相互独立,则A与,与B,与也都相互独立.
(4)若P(AB)=P(A)P(B),则A与B相互独立.
3.二项分布
(1)独立重复试验是指在相同条件下可重复进行的,各次之间相互独立的一种试验,在这种试验中每一次试验只有两种结果,即要么发生,要么不发生,且任何一次试验中发生的概率都是一样的.
(2)在n次独立重复试验中,用X表示事件A发生的次数,设每次试验中事件A发生的概率为p,则P(X=k)=,此时称随机变量X服从二项分布,记为X~B(n,p),并称p为成功概率.
4、均值与方差的常用性质:
(ⅰ)E(aξ+b)=aE(ξ)+b;E(ξ+η)=E(ξ)+E(η);D(aξ+b)=a2D(ξ);若已知随机变量ξ的均值、方差,求ξ的线性函数的均值、方差和标准差,可直接用ξ的均值、方差的性质求解.
(ⅱ) 若X服从二点分布,则E(X)=p,D(X)=pq. 一般地,若X~B(n,p),则E(X)=np,D(X)=np(1-p).
如能分析所给随机变量是服从常用的分布(如二点分布、二项分布等),可直接利用它们的均值、方差公式求解.
(ⅲ) 若X服从超几何分布,则E(X)=; 若X服从几何分布:E(X)=;D(X)=。
应用举例:
类型一、相互独立事件的概率
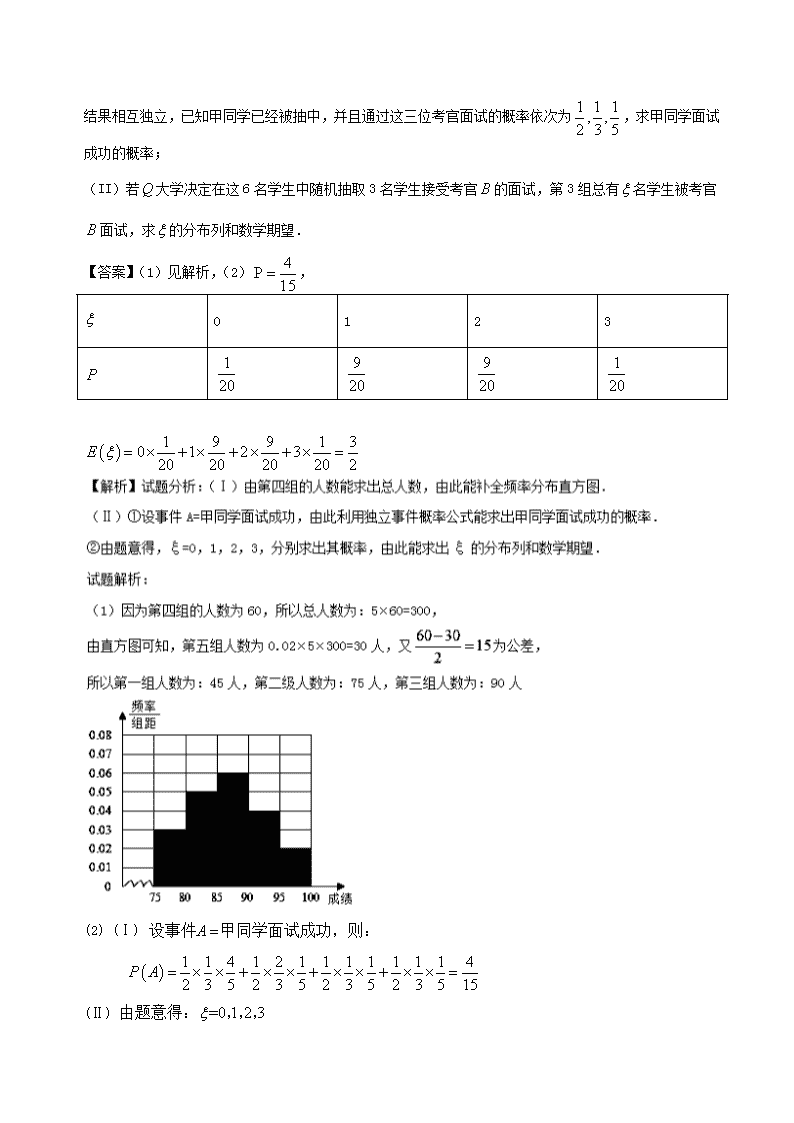
例1【2018届江西省南昌三中上第二次考试】在2017年高校自主招生期间,某校把学生的平时成绩按“百分制”折算,选出前名学生,并对这名学生按成绩分组,第一组,第二组,第三组,第四组,第五组,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为.
(1)请在图中补全频率分布直方图;
(2)若大学决定在成绩高的第组中用分层抽样的方法抽取6名学生进行面试
(I)若大学本次面试中有
三位考官,规定获得两位考官的认可即可面试成功,且各考官面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为,求甲同学面试成功的概率;
(II)若大学决定在这6名学生中随机抽取3名学生接受考官的面试,第3组总有名学生被考官面试,求的分布列和数学期望.
【答案】(1)见解析,(2),
0
1
2
3
(2) (Ⅰ)
(Ⅱ)
0
1
2
3
,
例2【2017四川模拟】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛,经过初赛,复赛,甲、乙两个代表队,(每队人)进入了决赛,规定每人回答一个问题,答对为本队赢得分,答错得分,假设甲队中每人答对的概率均为,乙队中人答对的概率分别为,且各人回答正确与否相互之间没有影响,用表示乙队的总得分.
(1)求的分布列和数学期望;
(2)求甲、乙两队总得分之和等于分且甲队获胜的概率.
【答案】(1)的分布列为
数学期望.(2).
;
.
的分布列为
.
点评:(1)相互独立事件是指两个试验中,两事件发生的概率互不影响;互斥事件是指同一次试验中,两个事件不会同时发生;
(2)求用“至少”表述的事件的概率时,先求其对立事件的概率往往比较简单.
类型二:求离散型随机变量的均值与方差
例3【2017浙江,8】已知随机变量满足P(=1)=pi,P(=0)=1—pi,i=1,2. 若0
C.>,< D.>,>
【答案】A
【解析】
,选A.
例4【2018届”超级全能生”高考全国卷26省9月联考】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取部进行测试,其结果如下:
甲种手机供电时间(小时)
乙种手机供电时间(小时)
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述部乙种手机中随机抽取部,记所抽
部手机供电时间不小于小时的个数为,求的分布列和数学期望.
【答案】(1)甲种手机电池质量更好(2)
(2)部乙种手机供电时间不小于小时的有部,小于小时的有部,所以得可能取值为,则,
故得分布列为
所以.
点评:求解该类问题,首先要理解问题的关键,其次要准确无误地找出随机变量的所有可能取值,计算出相应的概率,写出随机变量的分布列,正确运用均值、方差公式进行计算,也就是要过“三关”:①阅读理解关.②概率计算关.③公式应用关,如方差、均值公式要准确理解、记忆.
类型三、离散型随机变量均值与方差的应用
例5【2017课标3,理18】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
【答案】(1)分布列略;
(2) n=300时,Y的数学期望达到最大值,最大值为520元.
因此的分布列为
0.2
0.4
0.4
点评:(1)解决实际应用问题时,关键是正确理解随机变量取每一个值时所表示的具体事件.
(2)随机变量的均值反映了随机变量取值的平均水平,方差反映了随机变量稳定于均值的程度,它们从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据,一般先比较均值,若均值相同,再用方差来决定.
类型四、独立重复试验与二项分布
例6、设为随机变量,且,若随机变量的方差,则 ( )
A. B. C. D.
【答案】D
【解析】随机变量满足二项分布,所以n=6,所以 ,选D.
例7【2018届湖北省部分重点中络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
【答案】(1) (2)
点评:
(1)独立重复试验是在同样的条件下重复地、各次之间相互独立地进行的一种试验.在这种试验中,每一次试验只有两种结果,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的.
(2)二项分布满足的条件:
①每次试验中,事件发生的概率是相同的. ②各次试验中的事件是相互独立的.
③每次试验只有两种结果:事件要么发生,要么不发生.
④随机变量是这n次独立重复试验中事件发生的次数.
类型五、二项分布的均值与方差
例8【2018届云南省昆明市高新技术开发区高考适应性月考】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为15.
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设表示体重超过65公斤的学生人数,求的分布列及数学期望.
【答案】(1)60人;(2)详见解析.
∴的分布列为:
0
1
2
3
由于, .
例9【2018届广东省惠阳高级中学高三9月月考】某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
等级
一等品
二等品
三等品
次品
等级
一等品
二等品
三等品
次品
利润
表1 表2
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为元.
(1) 设随机抽取1件产品的利润为随机变量 ,写出的分布列并求出的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.
【答案】(1)(2)
试题解析:
设随机抽取1件产品的利润为随机变量,依题意得的分布列为:
点评:若X~B(n,p),则E(X)=np,D(X)=np(1-p).
方法、规律归纳:
1、利用均值、方差进行决策
均值能够反映随机变量取值的“平均水平”,因此,当均值不同时,两个随机变量取值的水平可见分晓,由此可对实际问题作出决策判断;若两随机变量均值相同或相差不大,则可通过分析两变量的方差来研究随机变量的离散程度或者稳定程度,进而进行决策.
2、求离散型随机变量均值的步骤
(1)理解随机变量X的意义,写出X可能取得的全部值;(2)求X的每个值的概率;
(3)写出X的分布列; (4)由均值定义求出E(X).
3、(1)D(ξ)表示随机变量ξ对E(ξ)的平均偏离程度.D(ξ)越大,表明平均偏离程度越大,说明ξ的取值越分散.反之D(ξ)越小,ξ的取值越集中在E(ξ)附近.统计中常用标准差 来描述ξ的分散程度.
(2)D(ξ)与E(ξ)一样也是一个实数,由ξ的分布列唯一确定.
(3)D(ξ)的单位与随机变量ξ的单位不同,而E(ξ)、 与ξ的单位相同.
(4)注意E(aX+b)=aE(X)+b,D(aX+b)=a2D(X).
实战演练:
1.袋中有大小相同的3只钢球,分别标有1、2、3三个号码,有放回的依次取出2个球,设两个球号码之和为随机变量,则所有可能值的个数是( )
A. 9 B. 8 C. 6 D. 5
【答案】D
【解析】根据题意,分析可得,这是有放回抽样,号码之和可能的情况为: ,共5种,故选D.
2. 已知离散型随机变量X的分布列为
则X的数学期望E(X)= ( )
A. B. 2 C. D.3
【答案】A.
【解析】,故选A.
3. 已知随机变量的分布列为
则( )
A. 1.32 B. 1.71 C. 2.94 D. 7.64
【答案】D
【解析】由题意,E(X)=-2×0.16+1×0.44+3×0.40=1.32,
∴E(2X+5)=2E(X)+5=2.64+5=7.64
4.设为随机变量, ,若随机变量的数学期望,则__________.(结果用分数表示)
【答案】
5.设随机变量,随机变量,若,则_________.
【答案】6
【解析】因,故,即,则,又随机变量,所以,
,应填答案.
6.一个袋中装有7个大小完全相同的球,其中4个白球,3个黄球,从中不放回地摸4次,一次摸一球,已知前两次摸得白球,则后两次也摸得白球的概率为________.
【答案】
【解析】前两次摸得白球,则剩下个白球, 个黄球
所以后两次也摸得白球的概率为
故答案为
7.某游戏的得分为1,2,3,4,5,随机变量表示小白玩游戏的得分.若=4.2,则小白得5分的概率至少为 .
【答案】
8.【2018届江西省赣州厚德外国语学校高三上第一次测试】一批产品的二等品率为,从这批产品中每次随机取一件,有放回地抽取次, 表示抽到的二等品件数,则____________.
【答案】1.96
【解析】由题意可得,抽到二等品的件数符合二项分布,即,由二项分布的期望公式可得.
9.【2018届浙江省源清中学高三9月月考】已知一个袋子中装有4个红球和2个白球,假设每一个球被摸到的可能性是相等的,若从袋子中摸出3个球,记摸到的白球的个数为,则的概率是_______;随机变量期望是_______.
【答案】 1
【解析】根据题意知ξ=0,1,2,
;
;
;
所以.
故答案为: .
10.【2017山东,理18】(本小题满分12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
【答案】(I)(II)X的分布列为
X
0
1
2
3
4
P
X的数学期望是.
得X的分布列为
X
0
1
2
3
4
P
进一步计算X的数学期望.
因此X的分布列为
X
0
1
2
3
4
P
X的数学期望是
=
11.【2017湖南】2016年8月21日第31届夏季奥运会在巴西里约闭幕,中国以26金18银26铜的成绩名称金牌榜第三、奖牌榜第二,某校体育爱好者协会在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下
表:
班号
一班
二班
三班
四班
五班
六班
频数
5
9
11
9
7
9
满意人数
4
7
8
5
6
6
(Ⅰ)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(Ⅱ)若从一班至二班的调查对象中随机选取2人进行追踪调查,记选中的4人中对“本届奥运会中国队
表现”不满意的人数为,求随机变量的分布列及其数学期望.
【答案】(Ⅰ);(Ⅱ)分布列见解析,.
(Ⅱ)的所有可能取值为0,1,2,3,
,
.
.
,
所以的分布列为:
0
1
2
3
所以的期望值为:.
12.【2016山东理19】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”
得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是,乙每轮猜对的概率是;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为的分布列和数学期望.
(2)由题意,随机变量的可能取值为.由事件的独立性与互斥性,
得 ,,
,
,