中考相似三角形综合题解析

中考相似三角形综合题解析

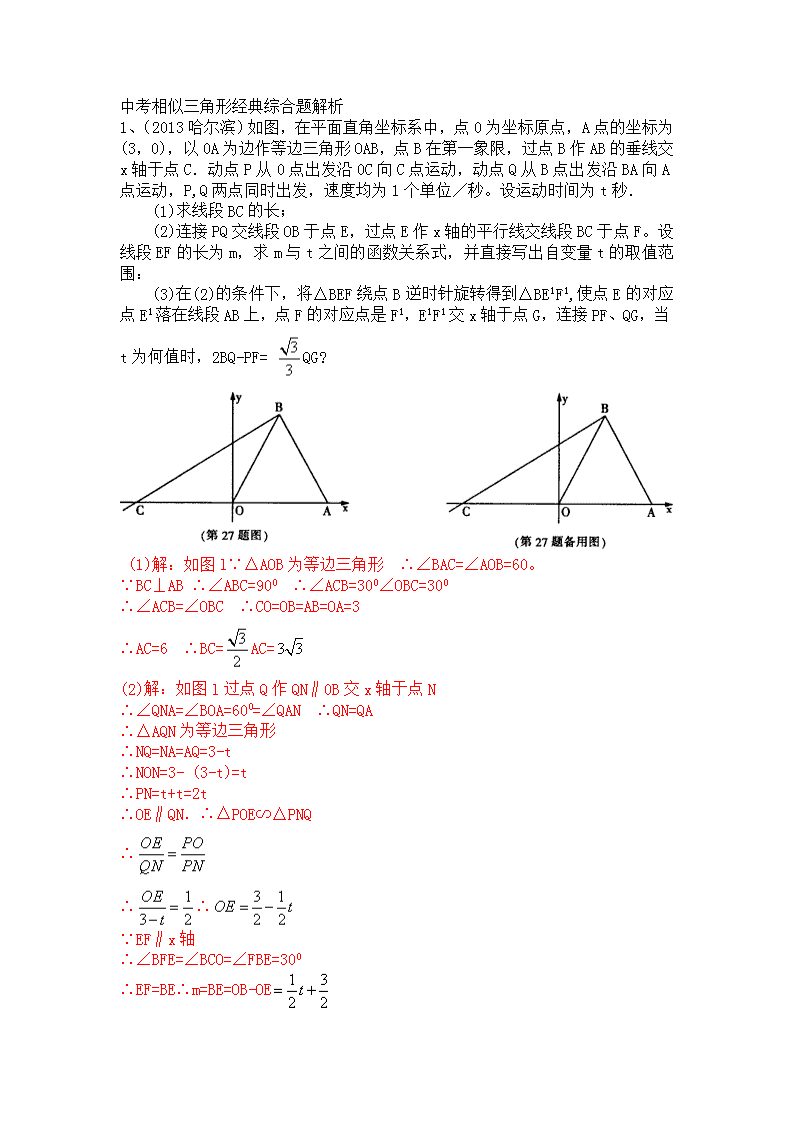
中考相似三角形经典综合题解析 1、（2013 哈尔滨）如图，在平面直角坐标系中，点 0 为坐标原点，A 点的坐标为 (3，0)，以 0A 为边作等边三角形 OAB，点 B 在第一象限，过点 B 作 AB 的垂线交 x 轴于点 C．动点 P 从 0 点出发沿 0C 向 C 点运动，动点 Q 从 B 点出发沿 BA 向 A 点运动，P,Q 两点同时出发，速度均为 1 个单位／秒。设运动时间为 t 秒． (1)求线段 BC 的长； (2)连接 PQ 交线段 OB 于点 E，过点 E 作 x 轴的平行线交线段 BC 于点 F。设 线段 EF 的长为 m，求 m 与 t 之间的函数关系式，并直接写出自变量 t 的取值范 围： (3)在(2)的条件下，将△BEF 绕点 B 逆时针旋转得到△BE1F1,使点 E 的对应 点 E1 落在线段 AB 上，点 F 的对应点是 F1，E1F1 交 x 轴于点 G，连接 PF、QG，当 t 为何值时，2BQ-PF= QG? (1)解：如图 l∵△AOB 为等边三角形 ∴∠BAC=∠AOB=60。 ∵BC⊥AB ∴∠ABC=900 ∴∠ACB=300∠OBC=300 ∴∠ACB=∠OBC ∴CO=OB=AB=OA=3 ∴AC=6 ∴BC= AC= (2)解：如图 l 过点 Q 作 QN∥0B 交 x 轴于点 N ∴∠QNA=∠BOA=600=∠QAN ∴QN=QA ∴△AQN 为等边三角形 ∴NQ=NA=AQ=3-t ∴NON=3- (3-t)=t ∴PN=t+t=2t ∴OE∥QN．∴△POE∽△PNQ ∴ ∴ ∴ ∵EF∥x 轴 ∴∠BFE=∠BCO=∠FBE=300 ∴EF=BE∴m=BE=OB-OE 3 3 3 2 3 3 OE PO QN PN = 1 3 2 OE t =− 3 1 2 2OE t= − 1 3 2 2t= + (0 ∴ 16 3x = y 8y =最大 6.已知正方形 ABCD 中，E 为对角线 BD 上一点，过 E 点作 EF⊥BD 交 BC 于 F，连 接 DF，G 为 DF 中点，连接 EG，CG． （1）求证：EG=CG； （2）将图①中△BEF 绕 B 点逆时针旋转 45º，如图②所示，取 DF 中点 G， 连接 EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立， 请说明理由． （3）将图①中△BEF 绕 B 点旋转任意角度，如图③所示，再连接相应的线 段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？ 解 ： （ 1 ） 证 明 ： 在 Rt △ FCD 中 ， ∵ G 为 DF 的 中 点 ， ∴ CG= FD．………………1 分 同理，在 Rt△DEF 中， EG= FD． ………………2 分 ∴ CG=EG．…………………3 分 （2）解：（1）证明：在 Rt△FCD 中， ∵G 为 DF 的中点， ∴ CG= FD． 同理，在 Rt△DEF 中， EG= FD． ∴ CG=EG． （2）（1）中结论仍然成立，即 EG=CG． 证法一：连接 AG，过 G 点作 MN⊥AD 于 M，与 EF 的延长线交于 N 点． 在△DAG 与△DCG 中， ∵ AD=CD，∠ADG=∠CDG，DG=DG， ∴ △DAG≌△DCG． ∴ AG=CG． 在△DMG 与△FNG 中， M N CB E F A A1 D F B A C E 图③ FB A D C E G 图① F B A D C E G 图② ∵ ∠DGM=∠FGN，FG=DG，∠MDG=∠NFG， ∴ △DMG≌△FNG． ∴ MG=NG 在矩形 AENM 中，AM=EN． 在 Rt△AMG 与 Rt△ENG 中， ∵ AM=EN， MG=NG， ∴ △AMG≌△ENG． ∴ AG=EG． ∴ EG=CG． 证法二：延长 CG 至 M,使 MG=CG， 连接 MF，ME，EC， 在△DCG 与△FMG 中， ∵FG=DG，∠MGF=∠CGD，MG=CG， ∴△DCG ≌△FMG． ∴MF=CD，∠FMG＝∠DCG． ∴MF‖CD‖AB． ∴ ． 在 Rt△MFE 与 Rt△CBE 中， ∵ MF=CB，EF=BE， ∴△MFE ≌△CBE． ∴∠MEC＝∠MEF＋∠FEC＝∠CEB＋∠CEF＝90°． ∴ △MEC 为直角三角形． ∵ MG = CG， ∴ EG= MC． （3）（1）中的结论仍然成立， 即 EG=CG．其他的结论还有:EG⊥CG． 7．如图，抛物线经过 三点． （1）求出抛物线的解析式； （2）P 是抛物线上一动点，过 P 作 轴，垂足为 M，是否存在 P 点，使 得以 A，P，M 为顶点的三角形与 相似？若存在，请求出符合条件的点 P 的坐标；若不存在，请说明理由； (4 0) (1 0) (0 2)A B C −，， ，， ， PM x⊥ OAC△ 【答案】解：（1） 该抛物线过点 ， 可设该抛物线的解析式为 ． 将 ， 代入， 得 解得 此抛物线的解析式为 ． （2）存在． 如图，设 点的横坐标为 ， 则 点的纵坐标为 ， 当 时， ， ． 又 ， ①当 时， ， 即 ． 解得 （舍去）， ．  (0 2)C −， ∴ 2 2y ax bx= + − (4 0)A ， (1 0)B ， 16 4 2 0 2 0 a b a b . + − =  + − = ， 1 2 5 2 a b .  = −  = ， ∴ 21 5 22 2y x x= − + − P m P 21 5 22 2m m− + − 1 4m< < 4AM m= − 21 5 22 2PM m m= − + − 90COA PMA∠ = ∠ = ° ∴ 2 1 AM AO PM OC = = APM ACO△ ∽△ 21 54 2 22 2m m m − = − + −   1 22 4m m= =， (21)P∴ ， ②当 时， ，即 ． 解得 ， （均不合题意，舍去） 当 时， ． 类似地可求出当 时， ． 当 时， ． 综上所述，符合条件的点 为 或 或 ． 8.如图，在 中，∠ACB= ,AC=6,BC=8,点 D 在边 AB 上运动，DE 平 分∠CDB 交边 BC 于点 E， 垂足为 M， 垂足为 N。 （1） 当 AD=CD 时，求证：DE∥AC； （2） 探究：AD 为何值时，△BME 与△CNE 相似？ （3） 探究：AD 为何值时，四边形 MEND 与△BDE 的面积相等？ （1）证明： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 又∵DE 是∠BDC 的平分线 ∴∠BDC=2∠BDE ∴∠DAC=∠BDE ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ∴DE∥AC ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）解：（Ⅰ）当 时，得 ∴BD=DC ∵DE 平分∠BDC ∴DE⊥BC，BE=EC. 又∠ACB=90° ∴DE∥AC. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 ∴ 即 ∴AD=5∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 （Ⅱ）当 时，得 1 2 AM OC PM OA = = APM CAO△ ∽△ 21 52(4 ) 22 2m m m− = − + − 1 4m = 2 5m = ∴ 1 4m< < (2 1)P ， 4m > (5 2)P −， 1m < ( 3 14)P − −， P (2 1)， (5 2)−， ( 3 14)− −， Rt ABC∆ 090 EM BD⊥ EN CD⊥ AD CD DAC DCA= ∴∠ = ∠ 2BDC DAC∴∠ = ∠ BME CNE△ ∽△ MBE NCE∠ = ∠ BE BD BC AB = 2 21 1 52 2BD AB AC BC= = + = BME ENC△ ∽△ EBM CEN∠ = ∠ 第 24 题 ∴EN∥BD 又∵EN⊥CD ∴BD⊥CD 即 CD 是△ABC 斜边上的高∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 由三角形面积公式得 AB·CD=AC·BC ∴CD= ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 综上，当 AD=5 或 时，△BME 与△CNE 相似. （3）由角平分线性质易得 即 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 ∴EM 是 BD 的垂直平分线. ∴∠EDB=∠DBE ∵∠EDB=∠CDE ∴∠DBE=∠CDE 又∵∠DCE=∠BCD ∴ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 ∙∙∙∙∙∙∙∙∙∙10 分 即 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 由 式得 9．如图，已知直线 与直线 相交于点 分别交 轴于 两点．矩形 的顶点 分别在直线 上，顶点 都在 轴上，且点 与点 重合． （1）求 的面积； （2）求矩形 的边 与 的长； （3）若矩形 从原点出发，沿 轴的反方向以每秒 1 个单位长度的速度平 1 2 8: 3 3l y x= + 2 : 2 16l y x= − + C l l1 2， 、 x A B、 DEFG D E、 1 2l l、 F G、 x G B ABC△ DEFG DE EF DEFG x 24 5 2 2 18 5AD AC CD= − = 18 5 1 2MDE DENS S DM ME= =△ △ · BDEMENDS S= △四边形 1 2 BD EM DM EM∴ =· · 1 2DM BD= CDE CBD△ ∽△ CD CE DE BC CD BD ∴ = = ① 2 CD BE BE BC BD BM ∴ = = 4BECD BM = 4 5cos 4 55 4 BMB CDBE = = ∴ = × = ① 2 25 8 CDCE BC = = 39 4 39 39cos8 5 8 10BE BM BE B∴ = ∴ = = × = 39 112 10 2 10 5AD AB BM∴ = − = − × = 第 24 题 移，设移动时间为 秒，矩形 与 重叠部分的面积为 ， 求 关于 的函数关系式，并写出相应的 的取值范围． 【答案】（1）解：由 得 点坐标为 由 得 点坐标为 ∴ 由 解得 ∴ 点的坐标为 ∴ （2）解：∵点 在 上且 ∴ 点坐标为 又∵点 在 上且 ∴ 点坐标为 ∴ （3）解法一： 当 时，如图 1，矩形 与 重叠部分为 五 边 形 （ 时 ， 为 四 边 形 ）．过 作 于 ， 则 (0 12)t t≤ ≤ DEFG ABC△ S S t t 2 8 03 3x + = ， 4x A= − ∴． ( )4 0− ， ． 2 16 0x− + = ， 8x B= ∴． ( )8 0， ． ( )8 4 12AB = − − = ． 2 8 3 3 2 16 y x y x  = +  = − + ， ． 5 6 x y =  = ， ． C ( )5 6， ． 1 1 12 6 362 2ABC CS AB y= = × × =△ · ． D 1l 2 88 8 83 3D B Dx x y= = ∴ = × + =， ． D ( )8 8， ． E 2l 8 2 16 8 4E D E Ey y x x= = ∴− + = ∴ =， ． ． E ( )4 8， ． 8 4 4 8OE EF= − = =， ． ① 0 3t <≤ DEFG ABC△ CHFGR 0t = CHFG C CM AB⊥ M Rt RtRGB CMB△ ∽ △ ． A D B E O C F x y y 1l y 2l （G） A D B E O R F x y y 1l y 2l M （图 3） G C A D B E O C F x y y 1l y 2l G （图 1） R M A D B E O C F x y y 1l y 2l G （图 2） R M ∴ 即 ∴ ∴ 即 当 时，如图 2，为梯形面积，∵G（8－t,0）∴GR= , ∴ 当 时，如图 3,为三角形面积， 10．如图，矩形 中， 厘米， 厘米（ ）．动点 同 时从 点出发，分别沿 ， 运动，速度是 厘米／秒．过 作直线垂 直于 ，分别交 ， 于 ．当点 到达终点 时，点 也随之停止 运动．设运动时间为 秒． （1）若 厘米， 秒，则 ______厘米； （2）若 厘米，求时间 ，使 ，并求出它们的相似比； （3）若在运动过程中，存在某时刻使梯形 与梯形 的面积相等，求 的取值范围； （4）是否存在这样的矩形：在运动过程中，存在某时刻使梯形 ，梯形 ，梯形 的面积都相等？若存在，求 的值；若不存在，请说明理 由． BG RG BM CM = ， 3 6 t RG= ， 2RG t= ． Rt RtAFH AMC △ ∽ △ ， ( ) ( )1 1 236 2 8 82 2 3ABC BRG AFHS S S S t t t t= − − = − × × − − × −△ △ △ ． 24 16 44 3 3 3S t t= − + + ． 83 <≤ t 3 283 8)8(3 2 tt −=+− 3 80 3 8]3 283 8)4(3 2[42 1 +−=−++−×= ttts 128 <≤ t 4883)12)(3 28(2 1 2 +−=−−= tttts ABCD 3AD = AB a= 3a > M N， B B A→ B C→ 1 M AB AN CD P Q， N C M t 4a = 1t = PM = 5a = t PNB PAD△ ∽△ PMBN PQDA a PMBN PQDA PQCN a D Q C P N BMA D Q C P N BMA E A D B C N M 【答案】解： （1） ， （2） ，使 ，相似比为 （3） ， ， 即 ， 当梯形 与梯形 的面积相等，即 化简得 ， ， ，则 ， （4） 时梯形 与梯形 的面积相等 梯形 的面积与梯形 的面积相等即可，则 ，把 代入，解之得 ，所以 ． 所以，存在 ，当 时梯形 与梯形 的面积、梯形 的面 积相等． 11.如图，四边形 ABCD 是正方形，△ABE 是等边三角形，M 为对角线 BD（不含 B 点）上任意一点，将 BM 绕点 B 逆时针旋转 60°得到 BN，连接 EN、AM、CM. ⑴ 求证：△AMB≌△ENB； ⑵ ①当 M 点在何处时，AM＋CM 的值最小； ②当 M 点在何处时，AM＋BM＋CM 的值最小，并说明理由； ⑶ 当 AM＋BM＋CM 的最小值为 时，求正方形的边长. 解： 3 4PM = 2t = PNB PAD△ ∽△ 3: 2 PM AB CB AB AMP ABC∠ = ∠ ⊥ ， ⊥ ， AMP ABC△ ∽△ PM AM BN AB ∴ = ( )PM a t t a tPMt a a − −= =， ( 1)3 t aQM a −∴ = − PMBN PQDA ( ) ( ) 2 2 QP AD DQ MP BN BM+ += ( )3 3 ( 1) ( ) 2 2 t a t ta a t t ta a −   − + − − +      = = 6 6 at a = + 3t ≤ 6 36 a a ∴ + ≤ 6 3 6a a∴ <≤ ， ≤ 3 6a< ≤ PMBN PQDA ∴ PQCN PMBN CN PM= ( ) 3t a t ta ∴ − = − 6 6 at a = + 2 3a = ± 2 3a = a 2 3a = PMBN PQDA PQCN 13 + ⑴∵△ABE 是等边三角形 ∴BA＝BE，∠ABE＝60°. ∵∠MBN＝60° ∴∠MBN－∠ABN＝∠ABE－∠ABN. 即∠BMA＝∠NBE. 又∵MB＝NB ∴△AMB≌△ENB（SAS） ⑵①当 M 点落在 BD 的中点时，AM＋CM 的值最小 ②连接 CE，当 M 点位于 BD 与 CE 的交点处时， AM＋BM＋CM 的值最小 理 由如下：连接 MN.由⑴知，△AMB≌△ENB ∴AM＝EN. ∵∠MBN＝60°，MB＝NB ∴△BMN 是等边三角形. ∴BM＝MN. ∴AM＋BM＋CM＝EN＋MN＋CM 根据“两点之间线段最短”，得 EN ＋MN＋CM ＝EC 最短 ∴当 M 点位于 BD 与 CE 的交点处时，AM＋BM＋CM 的值最小，即等于 EC 的 长 ⑶过 E 点作 EF⊥BC 交 CB 的延长线于 F ∴∠EBF＝90°－60°＝30° 设正方形的边长为 x，则 BF＝√3/2x，EF=x/2 在 Rt△EFC 中 ∵EF²＋FC²＝EC²， （x/2）²+（√3/2x+x）²=（√3+1）² 解得 x=√2 12．如图，已知△ABC 是边长为 6cm 的等边三角形，动点 P、Q 同时从 A、 B 两点出发，分别沿 AB、BC 匀速运动，其中点 P 运动的速度是 1cm/s，点 Q 运 动的速度是 2cm/s，当点 Q 到达点 C 时，P、Q 两点都停止运动，设运动时间为 t（s），解答下列问题： （1）当 t＝2 时，判断△BPQ 的形状，并说明理由； （2）设△BPQ 的面积为 S（cm2），求 S 与 t 的函数关系式； （3）作 QR//BA 交 AC 于点 R，连结 PR，当 t 为何值时，△APR∽△PRQ？ 【答案】 解：(1)△BPQ 是等边三角形,当 t=2 时,AP=2×1=2,BQ=2×2=4,所以 BP=AB-AP=6-2=4,所以 BQ=BP.又因为∠B=600,所以△BPQ 是等边三角形. (2) 过 Q 作 QE ⊥AB, 垂足为 E, 由 QB=2y, 得 QE=2t ·sin600= t, 由 AP=t, 得 PB=6-t, 所以 S△BPQ= ×BP×QE= (6-t)× t=－ t2+3 t； (3)因为 QR∥BA,所以∠QRC=∠A=600，∠RQC=∠B=600，又因为∠C=600, 所以△QRC 是等边三角形,所以 QR=RC=QC=6-2t.因为 BE=BQ·cos60 0= × 2t=t, 所以 EP=AB-AP-BE=6-t-t=6-2t,所以 EP∥QR,EP=QR,所以四边形 EPRQ 是平行 四边形, 所以 PR=EQ= t,又因为∠PEQ=90 0,所以∠APR=∠PRQ=90 0.因为△APR～△ PRQ, 所以∠QPR=∠A=600,所以 tan600= ,即 ,所以 t= , 所以当 t= 时, △APR～△PRQ 13．在直角梯形 OABC 中，CB∥OA，∠COA＝90º，CB＝3，OA＝6，BA＝ 3 5．分别以 OA、OC 边所在直线为 x 轴、y 轴建立如图 1 所示的平面直角 坐标系． （1）求点 B 的坐标； （2）已知 D、E 分别为线段 OC、OB 上的点，OD＝5，OE＝2EB，直线 DE 交 x 轴于点 F．求直线 DE 的解析式； （3）点 M 是（2）中直线 DE 上的一个动点，在 x 轴上方的平面内是否存在另 一个点 N．使以 O、D、M、N 为顶点的四边形是菱形？若存在，请求出点 N 的坐标；若不存在，请说明理由． 3 2 1 2 1 3 2 3 3 2 1 3 PR QR 3 3 26 =− t t 5 6 5 6 A B D E （第 26 题 图 1） F C O M N x y 图 7-2 A D O B C 2 1 M N 图 7-1 A D B M N 1 2 图 7-3 A D O BC 2 1 M N O 14．在图 15-1 至图 15-3 中，直线 MN 与线段 AB 相交 于点 O，∠1 = ∠2 = 45°． （1）如图 15-1，若 AO = OB，请写出 AO 与 BD 的数量关系和位置关系； （2）将图 15-1 中的 MN 绕点 O 顺时针旋转得到 图 15-2，其中 AO = OB． 求证：AC = BD，AC ⊥ BD； （3）将图 15-2 中的 OB 拉长为 AO 的 k 倍得到 图 15-3，求 的值． 【答案】 解：（1）AO = BD，AO⊥BD； （ 2 ） 证 明 ： 如 图 4 ， 过 点 B 作 BE∥CA 交 DO 于 E ， ∴∠ACO = ∠BEO． 又∵AO = OB，∠AOC = ∠BOE， ∴△AOC ≌ △BOE．∴AC = BE． 又 ∵∠1 = 45° ， ∴∠ACO = ∠BEO = 135°． ∴∠DEB = 45°． ∵∠2 = 45°，∴BE = BD，∠EBD = 90°．∴AC = BD． 延长 AC 交 DB 的延长线 于 F，如图 4．∵BE∥AC，∴∠AFD = 90°．∴AC⊥BD． （3）如图 5，过点 B 作 BE∥CA 交 DO 于 E，∴∠BEO = ∠ACO． 又∵∠BOE = ∠AOC ， ∴△BOE ∽ △AOC． ∴ ． 又∵OB = kAO， 由 （ 2 ） 的 方 法 易 得 BE = BD．∴ ． 15．如图，已知过 A（2，4）分别作 x 轴、y 轴的垂线，垂足分别为 M、N，若点 P 从 O 点出发，沿 OM 作匀速运动，1 分钟可到达 M 点，点 Q 从 M 点出发，沿 MA 作匀 速运动，1 分钟可到达 A 点。 AC BD AO BO AC BE = kA C B D = 图 4 A D O B C 2 1 M N E F A O B C1 D 2 图 5 M N E （1）经过多少时间，线段 PQ 的长度为 2？ （2）写出线段 PQ 长度的平方 y 与时间 t 之间的函数关系式和 t 的取值范围； （3）在 P、Q 运动过程中，是否可能出现 PQ⊥MN？若有可能，求出此时间 t；若不 可能，请说明理由； （4）是否存在时间 t，使 P、Q、M 构成的三角形与△MON 相似？若存在，求出此时 间 t；若不可能，请说明理由； Y N A Q O P M X 解：∵A（2，4）， ∴OM=2，AM=4， ∵点 P 从 O 点出发，沿 OM 作匀速运动，1 分钟可到达 M 点，点 Q 从 M 点出发，沿 MA 作匀速运动，1 分钟可到达 A 点， ∴点 P 的速度度 2，点 Q 速度的 4， （1）设经过 t 分钟线段 PQ 的长度是 2，则 PM=2-2t，QM=4t， 在 Rt△PQM 中， ∵PQ 2=PM2+QM2，即 22=（2-2t） 2+（4t） 2，解得 t=0（分）或 t=0.4 （分）． 答：当 t=0 或 t=0.4 时，线段 PQ 的长度为 2； （2）由（1）可知，PM=2-2t，QM=4t， 在 Rt△PQM 中，PQ 2=PM2+QM2，即 y=（2-2t） 2+（4t） 2， 整理得，y=20t 2-8t+4（0≤t≤1）； （3）存在． ∵A（2，4）， ∴N（0，4），M（2，0）， ∴ON=4，OM=2， 当△MON∽△PMQ 时， OM MP = ON MQ ，即 2 2−2t = 4 4t ，解得 t=0.5； 当△MON∽△QMP 时， OM MQ = ON MP ，即 2 4t = 4 2−2t ，解得 t=0.2． 故当 t=0.5 分或 t=0.2 分时 P、Q、M 构成的三角形与△MON 相似． 16、（2013•娄底压轴题）如图，在△ABC 中，∠B=45°，BC=5，高 AD=4，矩形 EFPQ 的一边 QP 在 BC 边上，E、F 分别在 AB、AC 上，AD 交 EF 于点 H． （1）求证： ； （2）设 EF=x，当 x 为何值时，矩形 EFPQ 的面积最大？并求出最大面积； （3）当矩形 EFPQ 的面积最大时，该矩形 EFPQ 以每秒 1 个单位的速度沿射线 DA 匀速向上运动（当矩形的边 PQ 到达 A 点时停止运动），设运动时间为 t 秒， 矩形 EFPQ 与△ABC 重叠部分的面积为 S，求 S 与 t 的函数关系式，并写出 t 的 取值范围． （1）证明：∵矩形 EFPQ， ∴EF∥BC，∴△AHF∽△ADC，∴ ， ∵EF∥BC，∴△AEF∽△ABC，∴ ， ∴ ． （2）解：∵∠B=45°，∴BD=AD=4，∴CD=BC﹣BD=5﹣4=1． ∵EF∥BC，∴△AEH∽△ABD，∴ ， ∵EF∥BC，∴△AFH∽△ACD，∴ ， ∴ ，即 ，∴EH=4HF， 已知 EF=x，则 EH=x． ∵∠B=45°，∴EQ=BQ=BD﹣QD=BD﹣EH=4﹣x． S 矩形 EFPQ=EF•EQ=x•（4﹣x）=﹣x2+4x=﹣（x﹣）2+5， ∴当 x=时，矩形 EFPQ 的面积最大，最大面积为 5． （3）解：由（2）可知，当矩形 EFPQ 的面积最大时，矩形的长为，宽为 4﹣×=2． 在矩形 EFPQ 沿射线 AD 的运动过程中： （I）当 0≤t≤2 时，如答图①所示． 设矩形与 AB、AC 分别交于点 K、N，与 AD 分别交于点 H1，D1． 此时 DD1=t，H1D1=2， ∴HD1=HD﹣DD1=2﹣t，HH1=H1D1﹣HD1=t，AH1=AH﹣HH1=2﹣t，． ∵KN∥EF，∴ ，即 ，得 KN=（2﹣t）． S=S 梯形 KNFE+S 矩形 EFP1Q1=（KN+EF）•HH1+EF•EQ1 = [（2﹣t）+]×t+（2﹣t） = t2+5； （II）当 2＜t≤4 时，如答图②所示． 设矩形与 AB、AC 分别交于点 K、N，与 AD 交于点 D2． 此时 DD2=t，AD2=AD﹣DD2=4﹣t， ∵KN∥EF，∴ ，即 ，得 KN=5﹣t． S=S△AKN=KN•AD2 =（5﹣t）（4﹣t） =t2﹣5t+10． 综上所述，S 与 t 的函数关系式为： S= ．