- 2021-05-22 发布 |
- 37.5 KB |
- 19页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
5年级数学教案《长方体和正方体的体积 》
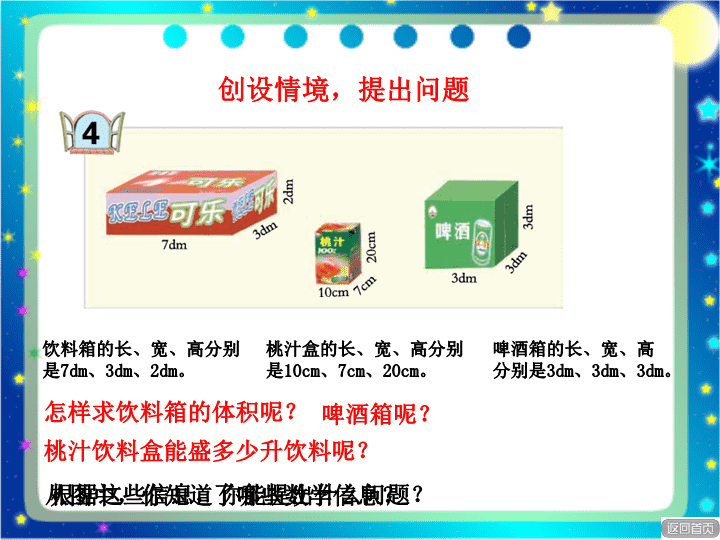
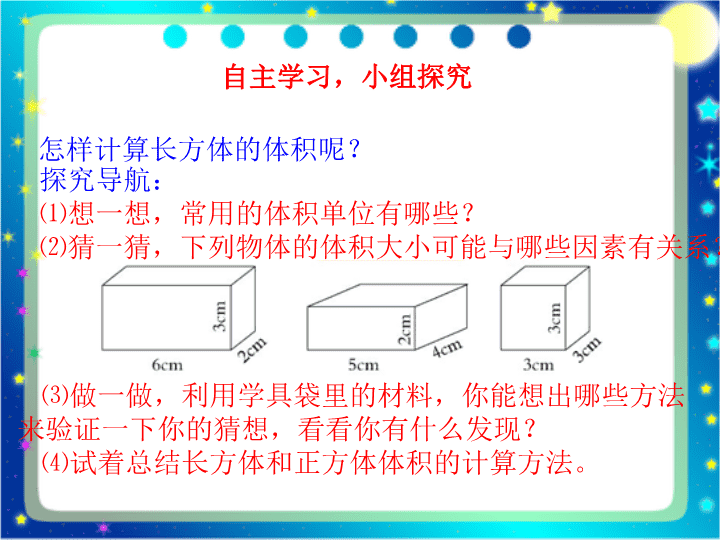
长方体和正方体体积 小学五年级数学 根据这些信息,你能提出什么问题? 从图中,你知道了哪些数学信息? 饮料箱的长、宽、高分别是 7dm 、 3dm 、 2dm 。 桃汁盒的长、宽、高分别是 10cm 、 7cm 、 20cm 。 啤酒箱的长、宽、高分别是 3dm 、 3dm 、 3dm 。 怎样求饮料箱的体积呢? 桃汁饮料盒能盛多少升饮料呢? 啤酒箱呢? 创设情境,提出问题 怎样计算长方体的体积呢? 探究导航: ⑴想一想,常用的体积单位有哪些? ⑵猜一猜,下列物体的体积大小可能与哪些因素有关系? ⑶做一做,利用学具袋里的材料,你能想出哪些方法来验证一下你的猜想,看看你有什么发现? ⑷试着总结长方体和正方体体积的计算方法。 自主学习,小组探究 怎样求可乐箱的体积呢?啤酒箱的体积呢? ( 1 )理解问题。 谈话:求一个长方体的体积大小就是求什么? 就是求这个长方体含有多少个体积单位 ( 2 )借助学具探究问题。 谈话:怎样才能知道它有多少个体积单位呢? 将你的想法和小组的同学交流一下。 汇报交流,评价质疑 小组合作: 用 1 立方厘米的小正方体,摆成这 3 种长方体,并把有关数据填入下表: 长方体 总个数 每排个数 每层排数 层数 ( 1 ) 6×2×3=36 (个) 6 2 3 ( 2 ) ( 3 ) ( 4 ) ( 5 ) … … 5X2X4=40( 个) 5 4 2 3X3X3=27( 个) 3 3 汇报交流,评价质疑 3 宽 2 厘米,一层可以摆 2 排。 高 3 厘米,可以摆 3 层。 ② 木块总数: 5×4×2=40 (个) 体积: 3×3×3=27 (立方厘米) ①长 6 厘米,一排可以摆 6 个。 体积: 6×2×3=36 (立方厘米) 体积: 5×4×2=40 (立方厘米) ③木块总数: 3×3×3=27 (个) 木块总数: 6×2×3=36 (个) 汇报交流,评价质疑 思考: 摆每个长方体的“总个数、每排个数、每层排数、层数”分别与这个长方体的“体积、长、宽、高”有什么关系? (同学们回答后,将表中“总个数、每排个数、每层排数、层数”下面写上“体积、长、宽、高”及相对应的单位。如下表) 总个数 每排个数 每层排数 层数 体积(立方厘米) 长(厘米) 宽(厘米) 高(厘米) ( 1 ) 6×2×3=36 (立方厘米) 6 厘米 2 厘米 3 厘米 ( 2 ) 5×4×2=40 (立方厘米) 5 厘米 4 厘米 2 厘米 ( 3 ) 3×3×3=27 (立方厘米) 3 厘米 3 厘米 3 厘米 汇报交流,评价质疑 归纳结论 ( 1 )猜想: 谈话:仔细观察表中的数据,你发现了什么规律?(可以动笔算一算)小组内交流。 长方体的体积 = 长 × 宽 × 高 ( 2 )验证结论: 谈话:同学们用小组合作的形式,通过拼摆、填表、思考、 观察、讨论并归纳出结论,大家非常聪明,但是,我们得出的 结论是否正确,还要接受实践的检验,我们用什么方法来验证 呢? 用测量 —— 计算;拼摆 —— 数一数的方法来验证 根据上面的结论,要计算长方体的体积必须知道什么条件? 长、宽、高 汇报交流,评价质疑 ( 3 )总结:长方体体积的计算方法,并概括出公式。 长方体的体积 = 长 × 宽 × 高 ( 4 )迁移:由于正方体是长、宽、高都相等的特殊的长方体, 所以正方体的体积计算公式应怎样表示? 正方体的体积 = 棱长 × 棱长 × 棱长 ( 5 )小结 汇报交流,评价质疑 运动会报名 男生志愿者 王东 李明 刘刚 李亮 丁一 张帅 于军 刘平 赵海 可乐箱的体积: 7×3×2 = 42 ( dm 3 ) 啤酒箱的体积: 3×3×3 = 27 ( dm 3 ) 你会求可乐箱的体积了吗? 啤酒箱的体积呢? 答:可乐箱的体积是 42 dm 3 答:啤酒箱的体积是 27 dm 3 抽象概括,总结提升 1. 推想体积公式 说一说长方体体积的计算方法,并概括出公式: 长方体的体积 = 长 × 宽 × 高 迁移:由于正方体是长、宽、高都相等的特殊的长方体,所以正方体的体积计算公式应怎样表示? 正方体的体积 = 棱长 × 棱长 × 棱长 2. 用字母表示体积公式: 在数学中,常用 a 表示长,用 b 表示宽,用 h 表示高,用 V 表示体积, 长方体体积计算公式用字母表示 V=abh 正方体的体积计算公式用字母表示 V=a·a·a ·a 可以写作 a3, 读作 a 的立方,表示 3 个 a 相乘。所以正方体的公式一般可以写成 V= a3 3. 探索体积公式“底面积 × 高”。 ( 1 )认识“底面”,引出“底面”概念。 “底面”一般指长方体、正方体的下面的面 ( 2 )巩固对底面的认识 请学生指出长方体可乐箱和正方体啤酒箱的底面 抽象概括,总结提升 ( 3 )认识底面积。 ① 认识了底面,那什么是底面积呢? 长方体和正方体底面的面积叫做它们的底面积。 ② 长方体的底面积如何计算?正方体的底面积如何计算? 长 × 宽实际就是长方体的底面积,棱长 × 棱长就是正方体的底面积,长方体的底面积 = 长 × 宽,正方体的底面积 = 棱长 × 棱长。 ( 4 )演变原来的体积公式。 已知底面积,怎样求长方体和正方体的体积呢? 长方体和正方体的体积计算公式可统一成: 长方体(正方体)的体积 = 底面积 × 高 如果用 S 表示底面积,上面的公式可以写成: V=Sh 抽象概括,总结提升 巩固应用,拓展提高 1 、课本自主练习第 1 题。 36 27 2 、自主练习 2 。 5 X 8 X 5 =40 X 5 =200( cm³ ) 4 X 4X 4 =16 X 4 =64( dm³ ) 20 X 4 X 5 =80 X 5 =400( m³ ) 巩固应用,拓展提高 3. 新课堂 98 页第 3 题。 一个长方体纸板箱的占地面积是 100 平方厘米,高 50 厘米。它的体积是多少立方厘米? 100 X 50 = 5000(m³ ) 答:它的体积是 5000m³ 巩固应用,拓展提高 4. 新课堂 98 页第 4 题。 把一个长 8 厘米、宽 5 厘米、高 4 厘米的长方体截成一个体积最大的正方体,这个正方体的体积是多少? 8 X 5 X 4 = 160(cm³ ) 答:这个正方体的体积是 160 cm³. 巩固应用,拓展提高 5. 自主练习第 3 题: 36.8 X 18.9 X 9.3 =695.52 X 9.3 =6468.336(cm³) 答:明代长城砖的体积是 6468.336 cm³. 巩固应用,拓展提高 回顾反思 通过本节课的学习,你有哪些收获?查看更多