2019届二轮复习选择填空题专练排列组合、二项式定理课件（46张）（全国通用）

2019届二轮复习选择填空题专练排列组合、二项式定理课件（46张）（全国通用）

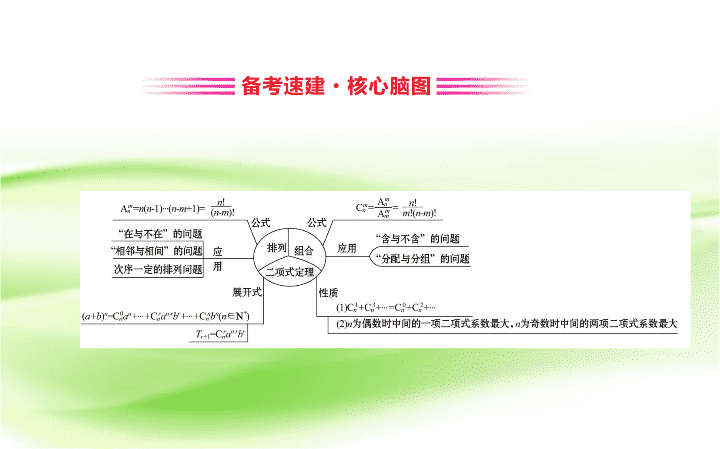
热点考向一 排列组合 考向剖析 : 本考向考题的形式是选择题与填空题 , 主要考查两个计数原理、排列、组合的简单应用 , 有时会与概率相结合 . 2019 年高考仍将以小题的形式呈现 , 特别关注与古典概型的结合 . 1. 若从 6 名志愿者中选 4 人去“鸟巢”和“水立方”实地培训 , 每处 2 人 , 其中乙不能去“水立方” , 则选派方法有 ( 　　 ) A.60 种　　　 B.70 种　　　 C.80 种　　　 D.90 种 【 解析 】 选 A. 若乙被选上 , 则乙不能去水立方 , 只能去 鸟巢 , 共有 种选派方法 , 若乙不被选上 , 共 有 种选派方法 , 所以共有 30+30=60 种选派方 法 . 2. 大数据时代出现了滴滴打车服务 , 二孩政策的放开使 得家庭中有两个小孩的现象普遍存在 , 某城市 , 关系要 好的 A,B,C,D 四个家庭各有两个小孩共 8 人 , 准备使用滴 滴打车软件 , 分别乘甲、乙两辆汽车出去游玩 , 每车限 坐 4 名 ( 乘同一辆车的 4 名小孩不考虑位置 ), 其中 A 户家 庭的孪生姐妹需乘同一辆车 , 则乘坐甲车的 4 名小孩恰 有 2 名来自于同一个家庭的乘坐方式共有 ( 　　 ) A.18 种 B.24 种 C.36 种 D.48 种 【 解题导引 】 分 2 种情况讨论 , 由分类计数原理计算可得答案 . 【 解析 】 选 B. 根据题意 , 分 2 种情况讨论 : ①A 户家庭的孪生姐妹在甲车上 , 甲车上剩下两个要来 自不同的家庭 , 可以在剩下的三个家庭中任选 2 个 , 再从 每个家庭的 2 个小孩中任选一个 , 来乘坐甲车 , 有 种乘坐方式 ; ②A 户家庭的孪生姐妹不在甲车上 , 需要在剩下的三个 家庭中任选 1 个 , 让其 2 个小孩都在甲车上 , 对于剩余的 2 个家庭 , 从每个家庭的 2 个小孩中任选一个 , 来乘坐甲车 , 有 种乘坐方式 ; 则共有 12+12=24 种乘坐方 式 . 3. 重阳节期间 , 学校准备举行慰问退休老教师晚会 , 学生们准备用歌曲、小品、相声三种艺术形式表演五个节目 , 其中歌曲有 2 个节目 , 小品有 2 个节目 , 相声有 1 个节目 , 要求相邻的节目艺术形式不能相同 , 则不同的编排种数为 ( 　　 ) A.96 B.72 C.48 D.24 【 解析 】 选 C. 第一类 , 先选择一个小品插入到 2 个歌曲 之间 , 另一个小品放在歌曲的两边 , 这时形成了 5 个空 , 将相声插入其中一个 , 故有 种 , 第二类 , 相 声插入歌曲之间 , 再把小品插入歌曲两边 , 有 种 , 第三类 , 相声插入小品之间 , 再把歌曲插入小品两边 , 有 种 , 根据分类计数原理可得 , 共有 40+4+4=48. 4. 从 1,3,5,7,9 中任取 2 个数字 , 从 0,2,4,6 中任取 2 个数字 , 一共可以组成 ________ 个没有重复数字的四位数 .( 用数字作答 )  【 解析 】 分类讨论 : 第一类 : 不含 0 的 , 按照分步乘法计 数原理 : 第二类 : 包含 0 的 , 按照分 步乘法计数原理 : 所以一共 有 1 260 个没有重复数字的四位数 . 答案 : 1 260 5. 若从 5 名学生中选出 4 名分别参加数学 , 物理 , 化学 , 生物四科竞赛 , 其中甲不能参加生物竞赛 , 则不同的参赛方案种数为 ( 　　 ) A.48 B.72 C.90 D.96 【 解析 】 选 D. 根据题意 , 从 5 名学生中选出 4 名分别参加 竞赛 , 分 2 种情况讨论 : ①, 选出的 4 人没有甲 , 即选出其他 4 人即可 , 有 种 情况 , ②, 选出的 4 人有甲 , 由于甲不能参加生物竞赛 , 则甲有 3 种选法 , 在剩余 4 人中任选 3 人 , 参加剩下的三科竞赛 , 有 种选法 , 则此时共有 3×24=72 种选法 , 则有 24+72=96 种不同的参赛方案 . 6. 某学校需要把 6 名实习老师安排到 A,B,C 三个班级去听课 , 每个班级安排 2 名老师 , 已知甲不能安排到 A 班 , 乙和丙不能安排到同一班级 , 则安排方案的种数有 ( 　　 ) A.24 B.36 C.48 D.72 【 解析 】 选 C. 根据题意 , 分 2 种情况讨论 : ①, 甲、乙、丙三人分在三个不同的班级 , 甲可以分在 B,C 班 , 有 2 种安排方法 , 将乙、丙全排列 , 分 在其他 2 个班级 , 有 种安排方法 , 剩余的 3 人 , 全排列 , 安排在三个班级 , 有 种安排方 法 , 则此时有 2×2×6=24 种安排方法 ; ②, 甲和乙、丙中的 1 人 , 分在同一个班级 , 在乙、丙中选出 1 人 , 和甲一起分在 B 班或 C 班 , 有 2×2=4 种情况 , 剩余 4 人 , 平均分成 2 组 , 有 种分组方法 , 再将 2 组全排列 , 对应剩下的 2 个班级 , 有 种安排方 法 , 则此时有 4×3×2=24 种安排方法 ; 则一共有 24+24=48 种安排方法 . 7.《 红海行动 》 是一部现代化海军题材影片 , 该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事 . 撤侨过程中 , 海军舰长要求队员们依次完成六项任务 , 并对任务的顺序提出了如下要求 : 重点任务 A 必须排在前三位 , 且任务 E,F 必须排在一起 , 则这六项任务的不同安排方案共有 ( 　　 ) A.240 种 B.188 种 C.156 种 D.120 种 【 解析 】 选 D. 根据题意 , 由于任务 A 必须排在前三位 , 分 3 种情况讨论 : ①,A 排在第一位 , 任务 E,F 必须排在一起 , 则任务 E,F 相邻的位置有 4 个 , 考虑两者的顺序 , 有 2 种情况 , 将剩下的 3 个任务全排列 , 安排在其他三个位置 , 有 种安排方法 , 则此时有 4×2×6=48 种安排方案 ; ②,A 排在第二位 , 任务 E,F 必须排在一起 , 则任务 E,F 相邻的位置有 3 个 , 考 虑两者的顺序 , 有 2 种情况 , 将剩下的 3 个任务全排列 , 安排在其他三个位置 , 有 种安排方法 , 则此时有 3×2×6=36 种安排方案 ; ③,A 排在第三位 , 任务 E,F 必须排在一起 , 则任务 E,F 相邻的位置有 3 个 , 考 虑两者的顺序 , 有 2 种情况 , 将剩下的 3 个任务全排列 , 安排在其他三个位置 , 有 种安排方法 , 则此时有 3×2×6=36 种安排方案 ; 则符合题意要求的安排方案有 36+36+48=120 种 . 【 名师点睛 】 1. 求解排列、组合问题的关注点 排组分清 , 加乘明确 ; 有序排列 , 无序组合 ; 分类相加 , 分步相乘 . 2. 排列、组合应用问题的常见解法 (1) 特殊元素 ( 特殊位置 ) 优先安排法 . (2) 相邻问题捆绑法 . 热点考向二 二项式定理 考向剖析 : 主要考查二项式定理中的通项、二项式系数、二项式特定项 ( 指定项 ), 以选择题、填空题为主 . 1.(2018· 西安一模 )(x 2 +2x+3y) 5 的展开式中 x 5 y 2 的系数为 ( 　　 ) A.60 B.180 C.520 D.540 【 解析 】 选 D.(x 2 +2x+3y) 5 可看作 5 个 (x 2 +2x+3y) 相乘 , 从中选 2 个 y, 有 种选法 ; 再从剩余的三个括号里边选 出 2 个 x 2 , 最后一个括号选出 x, 有 种选法 ; 所以 x 5 y 2 的系数为 2. 若 则 的展开式中常数项是 ( 　　 ) A.160 B.-160 C.-20 D.20 【 解析 】 选 的通项公式为 令 3-r=0, 即 r=3, 则常数项为 3. 若 的展开式中 x 3 项的系数为 20, 则实数 a=________.  【 解析 】 展开式的通项为 令 得 r=4, 所以 解得 a=4. 答案 : 4 4. 设 i 为虚数单位 , 则 (2i-x) 6 的展开式中含 x 4 项的系数 为 __________.  【 解析 】 (2i-x) 6 的展开式中含 x 4 项的系数为 答案 : -60 5.(2018· 天津高考 ) 在 的展开式中 ,x 2 的系 数为 ________.  【 解析 】 因为 的第 r+1 项 令 解得 r=2, 即 所以在 的展开式中 ,x 2 的系数为 答案 : 6.(2018· 南宁一模 )(x-2y)(2x+y) 5 的展开式中 ,x 2 y 4 的系数为 ________.  【 解析 】 根据 可得 (x-2y)(2x+y) 5 的展开式中 x 2 y 4 的系数为 答案 : -70 7.(2018· 唐山一模 )(2x-1) 6 的展开式中 , 二项式系数最大的项的系数是 ________( 用数字作答 ).  【 解析 】 (2x-1) 6 的展开式中 , 二项式系数最大的项是 其系数为 -160. 答案 : -160 【 名师点睛 】 与二项式定理有关的题型及解法 类型 解法 求特定项或其系数 常采用通项公式分析求解 系数的和或差 常用赋值法 近似值问题 利用展开式截取部分项求解 整除 ( 或余数 ) 问题 利用展开式求解