2021年成都市中考数学专题复习 二次函数中的线段最值+存在性问题 （北师大版）

2021年成都市中考数学专题复习 二次函数中的线段最值+存在性问题 （北师大版）

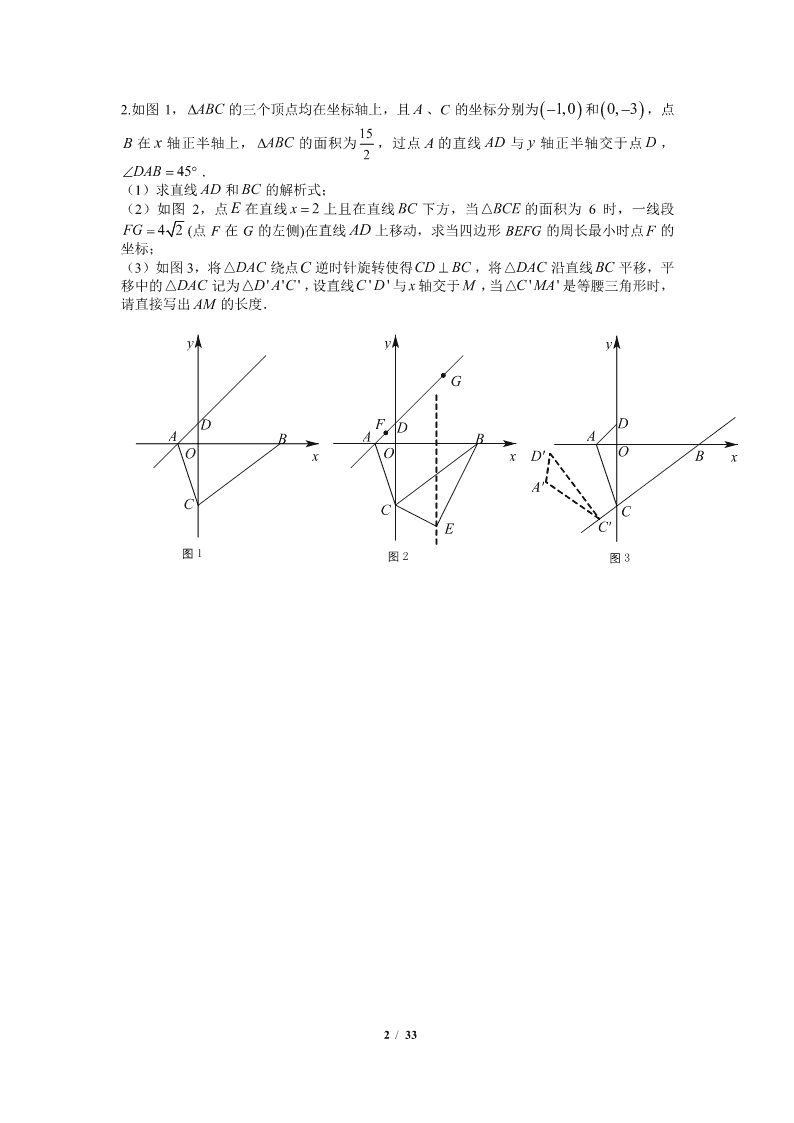
1 / 33 线段最值+存在性 1. 如图 1，抛物线 与 轴交于 A，B 两点（点 A 在点 B 的左 侧），与 轴交于点 C，直线 AE： 与抛物线相交于另一点 E，点 D 为抛物 线的顶点． （1）求直线 BC 的解析式及点 E 的坐标； （2）如图 2，直线 AE 上方的抛物线上有一点 P，过点 P 作 PF⊥BC 于点 F，过点 P 作平行 于 轴的直线交直线 BC 于点 G，当△PFG 周长最大时，在 轴上找一点 M，在 AE 上找一 点 N，使得 值最小，请求出此时 N 点的坐标及 的最 小值； （3）在第（2）问的条件下，点 R 为抛物线对称轴上的一点，在平面直角坐标系中是否存在 点 S，使以点 N，E，R，S 为顶点的四边形为矩形，若存在，请直接写出点 S 的坐标，若不 存在，请说明理由． 32 2 35 2 3 2 −+−= xxy x y 3 3 3 3 −= xy y y NEMNPM 2 1 ++ NEMNPM 2 1 ++ 图 1 图 2 2 / 33 2.如图 1， ABC 的三个顶点均在坐标轴上，且 A、C 的坐标分别为 ( )1,0− 和 ( )0, 3− ，点 B 在 x 轴正半轴上， ABC 的面积为 15 2 ，过点 A 的直线 AD 与 y 轴正半轴交于点 D ， 45DAB = ． （1）求直线 AD 和 BC 的解析式； （2）如图 2，点 E 在直线 2x = 上且在直线 BC 下方，当 BCE△ 的面积为 6 时，一线段 4 2FG = (点 F 在 G 的左侧)在直线 AD 上移动，求当四边形 BEFG 的周长最小时点F 的 坐标； （3）如图 3，将 DAC△ 绕点C 逆时针旋转使得CD BC⊥ ，将 DAC△ 沿直线 BC 平移，平 移中的 DAC△ 记为 ' ' 'D A C△ ，设直线 ' 'C D 与 x轴交于M ，当 ' 'C MA△ 是等腰三角形时， 请直接写出 AM 的长度． x y O D C B A 图 1 x y E O G F D C B A 图 2 图 3 A B C D O y x A' D' C' 3 / 33 3. 如图 1，在平面直角坐标系中，抛物线 与 x 轴交于 A、B 两点（点 A 在点 B 左侧），与 y 轴交于点 C. （1）如图 2，点 是是抛物线第二象限上一点，且满足 ，过点 作 的 平行线，分别与 x 轴、射线 交于点 、 ，,点 P 为直线 下方抛物线上的一动点， 连接 交线段 于点 ，当四边形 面积最大时，在 轴上找一点 ， 轴上找 一点 ，使得 取得最小值，并求出最小值； （2）如图 3，将 沿直线 平移得到 ''' COB ，再将 ''' COB 沿 ''CB 翻折得到 '''' COB ，连接 BC ' 、 BO '' ，则 ''' BOC 能否构成等腰三角形？若能，请直接写出所有 符合条件的点 ''O 的坐标；若不能，请说明理由. 22 2 3 4 2 2 −+= xxy D 22=− AD xx D AC CB F E AC PD AC Q PQEF y M x N NBMNPM 5 3 −+ BOC AC 4 / 33 4．如图 1，在平面直角坐标系中，抛物线 3 3 32 3 1 2 −+= xxy 与 x 轴交于 A， B 两点，交 y 轴于点 C，连接 BC．过点 A作 BC 的平行线交抛物线于点 D ． （1）求 ABC 的面积； （2）已知点M 是抛物线的顶点，在直线 AD 上有一动点 E ，x 轴上有一动点 F ，当 BEME + 最小时，求 CF EF− 的最大值及此时点 F 的坐标； （3）如图 2，在 y 轴正半轴上取点Q，使得 CQCB = ,点 P 是 轴x 上一动点，连接 PC ，将 CPQ 沿 PC 折叠至 CPQ ．连接 BQ， QB ， QQ ，当 QBQ  为等腰三角形时，直接写出 点 P 的坐标． x y M F E D C B AO 图 1 x y Q' Q P O D C B A 图 2 5 / 33 5．如图，抛物线 与 轴交于点 A，点 B，与 y 轴交于点 C，经过点 C 的直线 l 与抛物线交于另一点 E（4， ），抛物线顶点为 Q，抛物线对称轴与 x 轴交于 点 D． （1）求直线 CE 的解析式； （2）点 P 为直线 CE 下方抛物线上一动点，连接 PC，PE．当 的面积最大时，若 在 x 轴上存在动点 M，在 y 轴上存在动点 N，连接点 PM，PN，求 的 最小值； （3）连接 CD，将（1）中抛物线沿射线 CD 平移得到新抛物线 ， 经过点 D， 的 顶点为 H．在直线 QH 上是否存在点 G，使得 为等腰三角形？若存在，求出点 G 坐标． 图 1 图 2 图 3 23 2 3 3 3 3 y x x= − − x a PCE MNPNPM ++ 'y 'y 'y DQG y x y x y x Q D C BA O Q D C BA E O Q D C BA E O P 6 / 33 6．如图，在平面直角坐标系中，抛物线 21 2 y x bx c= − + + 与 x轴交于点 A B， ，与 y 轴交 于点C ，直线 BC 的解析式为 6y x= − + . （1）求抛物线的解析式； （2）点M 为线段 BC 上方抛物线上的任意一点，连接MB ，MC ，点 N 为抛物线对称轴上 任意一点，当M 到直线 BC 的距离最大时，求点M 的坐标及MN NB+ 的最小值； （3）在（2）中，点M 到直线 BC 的距离最大时，连接 OM 交 BC 于点 E，将原抛物线沿射 线 OM 平移，平移后的抛物线记为 y，当 y经过点 M 时，它的对称轴与 x 轴的交点记为 H．将 BOE 绕点 B 逆时针旋转 60°至 1 1BO E ，再将 1 1BO E 沿着直线 1O H 平移，得到 1 2 2B O E ．在平面内是否存在点 F，使以点C ，H ， 1B ，F 为顶点的四边形是以 1B H 为边 的菱形．若存在，直接写出点 1B 的横坐标；若不存在，请说明理由． x y O C BA M 备用图 x y E O C BA M 7 / 33 7．如图，抛物线 23 9 6 8 4 y x x= − + + 交 x 轴于 A、B 两点，点 A在点B 的右侧，交 y 轴于点C ， 点 D 为顶点． （1）求点 A、D 的坐标； （2）若点 P 是抛物线上位于第一象限内对称轴右侧的一个动点，当 45=ABPS 时，在线段 AC 上有一动点Q，当 QAPQ 5 3 + 的值最小时，求Q的坐标和 QAPQ 5 3 + 的最小值； （3）如图 2，点 F 是 y 轴上一点，且 2OF OB= ,连接BF 将 BOF 沿 x 轴向右平移，得 ' ' 'B O F ,当点 'F 恰好落在 AC 上时，连接 'OF ，将 'AOF 绕点 'F 顺时针旋转 (0 180 )     ，记旋转中的 'AOF 为 ' '' 'A O F ，在旋转过程中，设直线 ' ''A O 分 别与 x 轴、直线 AC 交于点M 、N ，当 AMN 是等腰三角形时，直接写出 AN 的值. 图 2 x F C B A O D y 8 / 33 8. 在平面直角坐标系中，二次函数 的图象与 轴交于 、 两点，与 轴 交于点 ，直线 经过点 ，与抛物线交于另一点 .已知 ， . （1）求抛物线与直线的解析式； （2）如图 1，若点 是 轴下方抛物线上一点，过点 作 于点 ，过点 作 轴交抛物线于点 ，过点 作 轴于点 ， 为直线 上一点，且 .点 为第四象限内一点，且在直线 上方，连接 、 、 .记 ， .当 取得最大值时，求出点 的坐标，并求出此时 的最小值. （3）如图 2，将点 沿直线 方向平移 13 个长度单位到点 ，过点 作 轴，交抛物线于点 .动点 为 轴上一点，连接 、 ，再将 沿直线 翻 折为 （点 、 、 、 在同一平面内），连接 、 、 ，当 为等腰三角形时，请直接写出点 的坐标. 图 1 图 2 82 −+= bxaxy x A B y C ( ) 5 0 3 y kx k= +  A R OAOC 2= OAOB 3= P x P ARPH ⊥ H P xPQ // Q P xHP ⊥ H  K HP  PQPK 32= I PQ IP IQ IK PQPHl 4 1 2 13 −= IKIQIPm ++= l P m A AR M M xMN ⊥ N D x MD DN MDN MD NMD  M N D N  AN NA  NN  NAN  D 9 / 33 9．如图 1，在平面直角坐标系中，抛物线 23 2 3 3 3 3 y x x= − + + 与 x 轴交于 A，B 两点（点 A在点 B 左侧），与 y 轴交于点C . （1）求直线 BC 的解析式； （2）点 P 是 BC 上方抛物线上的一个动点，过 P 作 PQ平行于 x 轴交 BC 于点Q，求线段PQ 的最大值； （3）如图 2，在（2）的条件下，当线段 PQ的长度最大时，连接 AC ，将 AOC 绕点O 逆时 针旋转60 得到 'O 'A C ，将 'O 'A C 沿 x 轴平移，记平移中的 'O 'A C 为 ''O' ''A C ，连接 ''A P 和 ''C P ，在平移过程中， '' ''A PC 是否能为等腰三角形，若能，请直接写出所有符合条件的 O'的坐标，若不能，请说明理由. 图 1 图 2 备用图 10 / 33 10．如图，抛物线 与 轴交于点 ， （点 在点 的左侧），与 轴 交于点 ，连接 ， ，过点 作 ∥ 交抛物线于点 ．点 为线 段 下方抛物线上的任意一点，过点 作 ∥ 轴交线段 于点 ． （1）如图 ，当 最大时，分别取线段 ， 上动点 ， ，使 ，若 点 为 的中点，点 为线段 上一动点，连接 ， ，求 的 最小值； （2）如图 ，点 在线段 上，且 ，连接 ，点 ， 分别是 与 线段 ， 的交点，以 为边，在 的右侧作矩形 ，其中 ．作 的角平分线 交 于点 ，将 绕点 顺时针旋转 得到 ， 当矩形 与 重叠部分（面积不为 ）为轴对称图形时，请直接写出点 横坐标的取值范围． 21 2 3 6 6 3 y x x= − − x A B A B y C AC BC A AD BC ( )8 3,10D P BC P PE y AD E 1 AEPE + AE AC G H 5GH = M GH N CB EN MN MNEN + 2 F AD : 7 :3AF DF = CF Q R PE CF BC RQ RQ RQTS 2RS = ACB CK AD K ACK C 75 ' 'A CK RQTS ' 'A CK 0 P 第 26 题图 1 A NH C G E P D y x O M B A F C E P 'K D xBQ R T y 'A K S O 第 26 题图 2 A F C 'K D xB y 'AO 第 26 题备用图 11 / 33 11．如图，抛物线 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴 交于点 C，连接 AC、BC．点 D 是线段 AB 上一点，且 AD＝CA，连接 CD． （1）点 P 是直线 BC 上方抛物线上的一动点，在线段 BC 上有一动点 Q，连接 ， 当△PCD 的面积最大时，求 的最小值； （2）将过点 的直线 绕点 旋转，设旋转中的直线 分别与直线 AC、直线 CO 交于点 M、 N，当 CMN 为等腰三角形时，求此时 CM 的长． 26 题图 备用图 21 1 4 3 3 y x x= − + + , ,PC PD PQ 10PQ CQ+ D l D l  x y D B C A O P Q x y D B C A O 12 / 33 12．抛物线 21 3 6 12 6 = − − +y x x 与 x轴交于点 A， B （点 A在点 B 的左侧），与 y 轴交于 点C ，点D与点C 关于抛物线的对称轴对称，连接BD交 y 轴于点G ，作直线OD ，点 P 为线段 BD 上方的抛物线上任意一点，过点 P 作 PE ∥ y 轴交 BD 于点 E ，过点 P 作 ⊥PF 直线OD 于点 F ． （1）如图1，当 +2PE PF 最大时，点M 为平面上一点，且MCG 是以M 为直角顶点的直 角三角形，动点Q 从点 E 出发，沿射线 ED方向以每秒 2 3 3 个单位长度的速度运动到点 N 处，然后以每秒 个单位长度的速度沿着适当路径运动到直线OD 上的点 R 处，最后以 每秒 个单位长度的速度沿着适当路径到点 M 处停止运动，求动点Q 在整个运动过程中 的最短用时； （2）如图 2，连接CD ，将 OCD 沿射线DB方向平移至 ''' DCO 的位置，当线段 ' 'O D 的中点 H 落在 x 轴上时，此时再将 ''' DCO 绕平面内某点 K 旋转 90 ，旋转后的三角形 记为 '''''' DCO ，若 '''''' DCO 恰好有两个顶点同时落在抛物线上，请直接写出满足条件 的点 K 的坐标. 1 1 图 1 图 2 13 / 33 13．已知抛物线 与 x 轴交于 A，B 两点（点 在点 的左侧），与 y 轴交 于点 C． （1）如图 1，点 为线段 上方抛物线上的任意一点，当四边形 面积最大时，连接 并延长至点 ，使 ，在对称轴上有一动点 ，将△ 沿边 翻折得到△ ，取 的中点 ，求 的最大值； （2）如图 2，将△ 绕点 顺时针旋转至△ 的位置，点 ， 的对应点分别为 ， ，且点 落在线段 上，再将△ 沿 轴平移得△ ，其中直线 与 轴 交于点 ，点 是抛物线对称轴上的动点，连接 ， ，△ 能否成为以 为直 角边的等腰直角三角形？若能，请直接写出所有符合条件的点 的坐标；若不能，请说明理 由． 21 2 3 9 9 3 y x x= − + + A B P BC PCAB OP Q PQ OP= E ACE CE 'A CE 'BA N BQ QN+ AOC O 1 1A OC A C 1A 1C 1A AC 1 1A OC y 2 1 2A O C 1 2O C x K T KT 1O T 1O KT 1O K T 图 1 N O Q A' P E C BA y x 图 2 O1 C2 C1 A2 A1 T K O C BA y x 14 / 33 14．抛物线 21 3 4 4 2 y x x= − + + 与 x 轴交于点 A，B（ A在 B 左边），与 y 轴交于点C ，点 D 与点C 关于抛物线对称轴对称． （1）如图1，连接 AD ，P 是 AD 上方抛物线上一动点，连接 AP ，DP，当 APD△ 面积最 大时，过点 B 作 BE ∥ AD 交 y 轴于点 E ，在直线 AD 上有一动点M ，过点M 作 MN BE⊥ 于点 N ，连接 PM ， 求 5 5 PM MN BN+ + 的最小值； （2）如图 2，将 AOC△ 绕点O 顺时针旋转60得到 A OC △ ，将 A OC △ 沿直线OC平移， 记平移中的 A OC △ 为 A O C  △ ，直线 A O 与 x轴交于点 F ，将 FO C △ 沿直线OC 翻折得到 F O C  △ ，当 CC F △ 为等腰三角形时，求点 F 的坐标． 图 1 图 2 15 / 33 15. 17 / 33 17. 18 / 33 18. 19 / 33 19．如图，已知直线 lAC：y=﹣ 交 x 轴、y 轴分别为 A、C 两点，直线 BC⊥AC 交 x 轴于点 B． （1）求点 B 的坐标及直线 BC 的解析式； （2）将△OBC 关于 BC 边翻折，得到△O′BC，过点 O′作直线 O′E 垂直 x 轴于点 E，F 是 y 轴上一点，P 是直线 O′E 上任意一点，P、Q 两点关于 x 轴对称，当|PA﹣PC|最大时，请 求出 QF+ FC 的最小值； （3）若 M 是直线 O′E 上一点，且 QM=3 ，在（2）的条件下，在平面直角坐标系中，是 否存在点 N，使得以 Q、F、M、N 四点为顶点的四边形是平行四边形？若存在，请直接 写出点 N 的坐标；若不存在，请说明理由． 20 / 33 20. 平面直角坐标系中，直线 xy = ，点 )610( ，Q ，点 )0, 10 7 (A ，动点M 在直线 )0( = xxy 上，动点 P 、 N 在 x 轴正半轴上，连接MQ 、MN 、 NQ . （1）若点 )77( ，M ，求直线MQ 的解析式； （2）如图 1，当 QMN 周长最小时，连接MP ，求 MQPMAP ++ 5 3 的最小值，并求出 此时点 P 的坐标； （3）如图 2，在第（2）问条件下，将 PMN 绕点 A旋转 度（ 3600  ），得 NMP  ， 记旋转过程中直线 PM  与直线 xy = 交于点 K ，直线 PM  与 x 轴交于点 R ，是否存在 OKR 为等腰直角三角形，若存在，直接写出线段 KR 的长度；若不存在，请说明理由. 图 1 图 2 21 / 33 21. 22 / 33 22. 23 / 33 23. 24 / 33 24.如图 1，抛物线与 21 1 4 3 3 y x x= − + + 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C，连接 AC、BC，点 D 是线段 AB 上一点，且 AD = CA，连接 CD． (1) 求直线 CD 的解析式； (2) 如图 2，点 P 是直线 BC 上方抛物线上的一动点，在线段 BC 上有一动点 Q，连接 PC、PD、PQ，当△PCD 面积最大时，求 10 10 PQ CQ+ 的最小值； (3) 将过点 D 的直线 l 绕点 D 旋转，设旋转中的直线 l 分别与直线 AC、直线 CO 交于 点 M、N，当△CMN 为等腰三角形时，直接写出 CM 的长． 图 1 图 2 备用图 25 / 33 25. 27 / 33 27. 28 / 33 28. 29 / 33 29. 30 / 33 30. 31 / 33 31. 32 / 33 32. 33 / 33 33．如图 1，抛物线 32 −= xy 与 x 轴交于 A、B 两点（点 A 在点 B 的右侧），与 y 轴交于点 C，连接 AC．点 Q 是线段 AC 上的动点，过 Q 作直线 xl // 轴，直线 l 与 BAC 的平分 线交于点 M ，与 CAx 的平分线交于点 N． （1）P 是直线 AC 下方抛物线上一动点，连接 PA，PC．当 PAC 的面积最大时，求 AMPQ 2 1 + 的最小值； （2）如图 2，连接 MC，NC，当四边形 AMCN 为矩形时，将 AMN 沿着直线 AC 平移得到 ''' NMA ，边 A’M’所在的直线与 y 轴交于 D 点，若 ''NDM 为等腰三角形时，求 OD 的 长。 图 1 y x l O NM Q P C B A y xO NM Q C B A 图 2