- 2021-05-22 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
探索直线平行的条件教案(1)
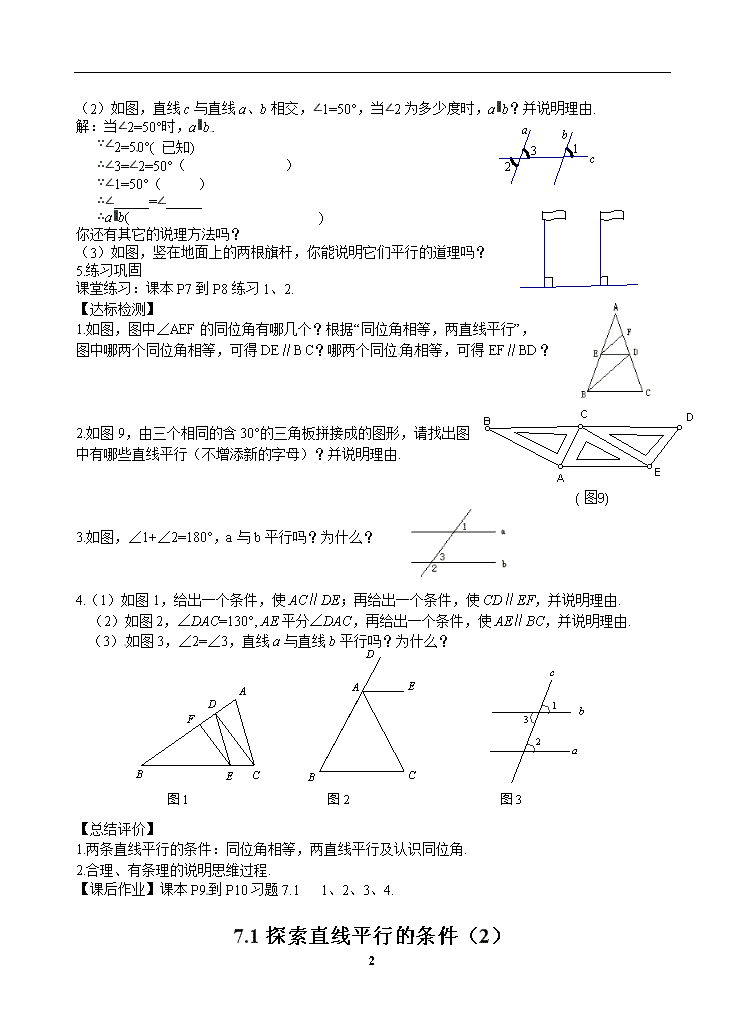
7.1探索直线平行的条件(1) 学习目标: 1.经历探索直线平行的条件“同位角相等,两直线平行”,认识同位角. 2.经历观察、操作、想象、说理、交流等数学活动,发展空间观念和有条理地表达能力. 学习重点: 1.会正确识别图形中的同位角. 2.掌握直线平行的条件“同位角相等,两直线平行”. 3.发展空间观念和有条理地表达能力. 学习难点:有条理地表达出问题分析和解决的过程. 导学过程: 【预习交流】 1.预习课本P6页到P8页,有哪些疑惑? 2.下面的图形中,直线a、b被c所截,所标出的角中有哪些角是同位角?同位角一定相等吗? a b c 5 6 4 8 1 2 3 7 【点评释疑】 1.课本P6操作. 2.课本P6说一说. 两条直线被第三条直线所截,在二条直线的同侧,且在第三条直线的同旁的二个角叫同位角. 同位角的特征:①∠1、∠2分别在直线a、b的同侧(上方),并且都在直线c的同旁. ②基本形状是“F”型. 想一想:在上面的图形中,还有没有其他的同位角? 归纳:同位角相等,两直线平行. B A C D 1 2 3.例1.如图:∠1=∠C,∠2=∠C,请找出图中互相平行的直线,并说明理由. 解:(1)AB∥CD ∵∠1=∠C( ) ∴AB∥CD( ) (2)AC∥BD ∵∠2=∠C( ) ∴AC∥BD ( ) 4.应用探究 (1)如图,①∠2与∠4是直线 、 被直线 所截成的同位角; ②∠3与 是同位角. 4 (2)如图,直线c与直线a、b相交,∠1=50°,当∠2为多少度时,a∥b?并说明理由. 解:当∠2=50°时,a∥b. ∵∠2=50°( 已知) ∴∠3=∠2=50°( ) ∵∠1=50°( ) ∴∠ =∠ ∴a∥b( ) 你还有其它的说理方法吗? (3)如图,竖在地面上的两根旗杆,你能说明它们平行的道理吗? 5.练习巩固 课堂练习:课本P7到P8练习1、2. 【达标检测】 1.如图,图中∠AEF的同位角有哪几个?根据“同位角相等,两直线平行”, 图中哪两个同位角相等,可得DE∥BC?哪两个同位角相等,可得EF∥BD? 2.如图9,由三个相同的含30°的三角板拼接成的图形,请找出图 中有哪些直线平行(不增添新的字母)?并说明理由. 3.如图,∠1+∠2=180°,a与b平行吗?为什么? 4.(1)如图1,给出一个条件,使AC∥DE;再给出一个条件,使CD∥EF,并说明理由. (2)如图2,∠DAC=130°, AE平分∠DAC,再给出一个条件,使AE∥BC,并说明理由. 图1 图2 图3 (3)如图3,∠2=∠3,直线a与直线b平行吗?为什么? 【总结评价】 1.两条直线平行的条件:同位角相等,两直线平行及认识同位角. 2.合理、有条理的说明思维过程. 【课后作业】课本P9到P10习题7.1 1、2、3、4. 7.1探索直线平行的条件(2) 4 学习目标: 1.能抓住内错角、同旁内角的特征识别内错角和同旁内角. 2.会用内错角相等、同旁内角互补判定二条直线平行. 学习重点:会用内错角相等、同旁内角互补判定二条直线平行. 图1 c 学习难点:有条理地思考和表达过程. 导学过程: 【预习交流】 1.预习课本P7页到P9页,有哪些疑惑? 2.如图1,∠C=31°,当∠ABE= 度时,就能使BE//CD. . 3.上图中∠1和∠2是同位角的是( ) A.⑴、⑵、⑶ B.⑵、⑶、⑷ C.⑶、⑷、⑸ D.⑴、⑵、⑸ 4.如图,已知直线AB、CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP,为什么? . 【点评释疑】 1.课本P7议一议. 两条直线被第三条直线所截,在二条直线的内侧,且在第三条直线的两旁的二个角叫内错角. 2 B A C D F E 1 两条直线被第三条直线所截,在两条直线的内侧,且在第三条直线的同旁的两个角叫同旁内角. 内错角相等,两直线平行. 同旁内角互补,两直线平行. 2.如图,∠1=∠2,∠B+∠BDE=180,图中那些线互相平行,为什么? 解:(1)AB∥EF ∵∠1=∠2( ) ∴AB∥EF ( ) (2)DE∥BC ∵ ( ) ∴DE∥BC ( ) 3.如图、点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断 BE与AC的位置关系吗?请说明理由. 4 4.应用探究 (1)如图1,与∠1是同位角的角是 ,与∠1是内错角的角是 ,与∠1是同旁内角的角是 . 图1 图2 图3 图4 (2)如图2,∠ _ 与∠C是直线 _ 与 _ 被直线 _ 所截得的同位角,∠ __ 与∠3是直线 _ 与 被直线 _ 所截得的内错角,∠ _ 与∠A是直线AB与BC被直线 _ 所截得的同旁内角. (3)如图3,①如果∠B =∠1,那么根据___________________________,可得AD∥BC; ②如果∠D =∠1,那么根据___________________________,可得AB∥CD. (4)如图4,下列条件中能判定DE∥AC的是( ) A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2 (5)已知:如图,∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC. 求证AE∥BC 5.练习巩固 课堂练习:课本P9练习1、2、3. 【达标检测】 1.如图,下列说法正确的是( ) A.∠2和∠4是同位角 B.∠2和∠4是内错角C.∠1和∠A是内错角 D.∠3和∠4是同旁内角 A C E B D 2.如图,能判断EB∥AC的条件是( )A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠A=∠ABE 3.如图、直线EF过点A,D是BA延长线上的点,当具备什么 条件时,可以判定EF∥BC?为什么? 【总结评价】 1.内错角相等、同旁内角互补 同位角相等 平行 2.合理、有条理的说明思维过程. 【课后作业】课本P10习题7.1 5、6、7、8. 4查看更多