【物理】2020届一轮复习人教版功能关系　能量守恒定律课时作业

【物理】2020届一轮复习人教版功能关系　能量守恒定律课时作业

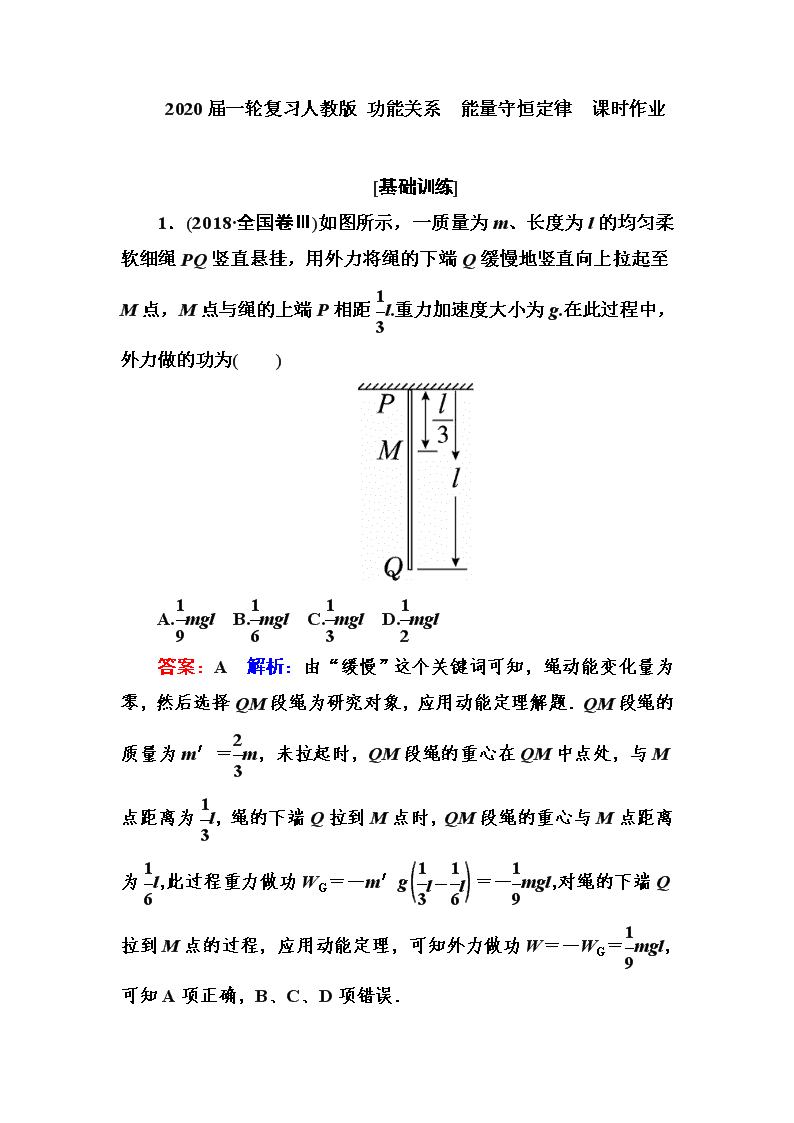
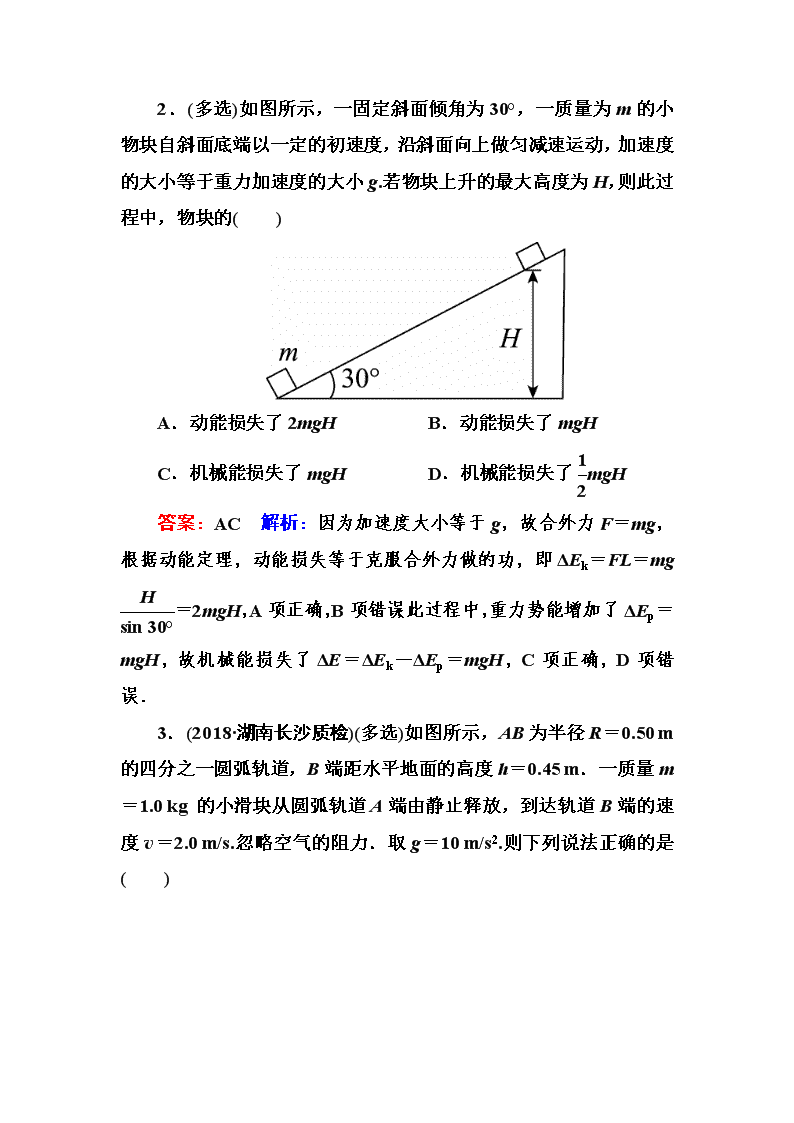
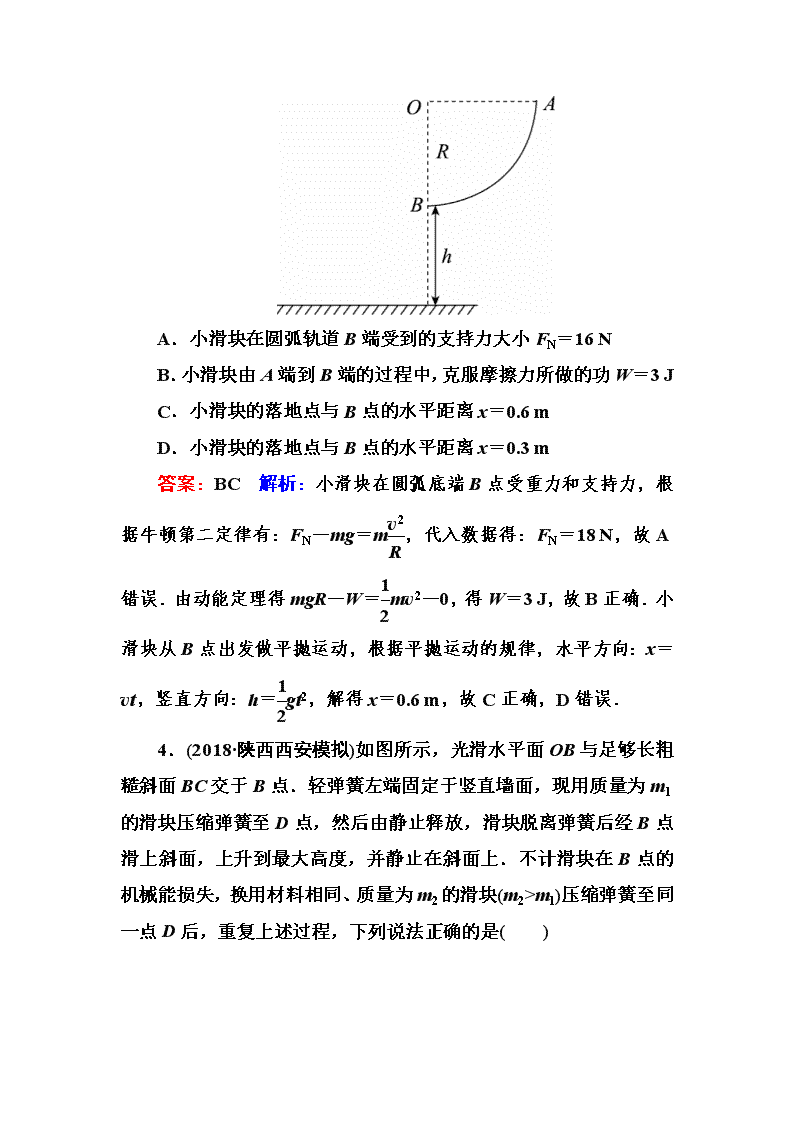
‎2020届一轮复习人教版 功能关系　能量守恒定律 课时作业 ‎　　　　　　　　　　　　　　　　‎ ‎[基础训练]‎ ‎1．(2018·全国卷Ⅲ)如图所示，一质量为m、长度为l的均匀柔软细绳PQ竖直悬挂，用外力将绳的下端Q缓慢地竖直向上拉起至M点，M点与绳的上端P相距l.重力加速度大小为g.在此过程中，外力做的功为(　　)‎ A.mgl B.mgl C.mgl D.mgl 答案：A　解析：由“缓慢”这个关键词可知，绳动能变化量为零，然后选择QM段绳为研究对象，应用动能定理解题．QM段绳的质量为m′＝m，未拉起时，QM段绳的重心在QM中点处，与M点距离为l，绳的下端Q拉到M点时，QM段绳的重心与M点距离为l，此过程重力做功WG＝－m′g＝－mgl，对绳的下端Q拉到M点的过程，应用动能定理，可知外力做功W＝－WG＝mgl，可知A项正确，B、C、D项错误．‎ ‎2．(多选)如图所示，一固定斜面倾角为30°，一质量为m 的小物块自斜面底端以一定的初速度，沿斜面向上做匀减速运动，加速度的大小等于重力加速度的大小g.若物块上升的最大高度为H，则此过程中，物块的(　　)‎ A．动能损失了2mgH B．动能损失了mgH C．机械能损失了mgH D．机械能损失了mgH 答案：AC　解析：因为加速度大小等于g，故合外力F＝mg，根据动能定理，动能损失等于克服合外力做的功，即ΔEk＝FL＝mg＝2mgH，A项正确，B项错误；此过程中，重力势能增加了ΔEp＝mgH，故机械能损失了ΔE＝ΔEk－ΔEp＝mgH，C项正确，D项错误．‎ ‎3．(2018·湖南长沙质检)(多选)如图所示，AB为半径R＝‎0.50 m 的四分之一圆弧轨道，B端距水平地面的高度h＝‎0.45 m．一质量m＝‎1.0 kg 的小滑块从圆弧轨道A端由静止释放，到达轨道B端的速度v＝‎2.0 m/s.忽略空气的阻力．取g＝‎10 m/s2.则下列说法正确的是(　　)‎ A．小滑块在圆弧轨道B端受到的支持力大小FN＝16 N B．小滑块由A端到B端的过程中，克服摩擦力所做的功W＝3 J C．小滑块的落地点与B点的水平距离x＝‎‎0.6 m D．小滑块的落地点与B点的水平距离x＝‎‎0.3 m 答案：BC　解析：小滑块在圆弧底端B点受重力和支持力，根据牛顿第二定律有：FN－mg＝m，代入数据得：FN＝18 N，故A错误．由动能定理得mgR－W＝mv2－0，得W＝3 J，故B正确．小滑块从B点出发做平抛运动，根据平抛运动的规律，水平方向：x＝vt，竖直方向：h＝gt2，解得x＝‎0.6 m，故C正确，D错误．‎ ‎4．(2018·陕西西安模拟)如图所示，光滑水平面OB与足够长粗糙斜面BC交于B点．轻弹簧左端固定于竖直墙面，现用质量为m1的滑块压缩弹簧至D点，然后由静止释放，滑块脱离弹簧后经B点滑上斜面，上升到最大高度，并静止在斜面上．不计滑块在B点的机械能损失，换用材料相同、质量为m2的滑块(m2>m1)压缩弹簧至同一点D后，重复上述过程，下列说法正确的是(　　)‎ A．两滑块到达B点时速度相同 B．两滑块沿斜面上升的最大高度相同 C．两滑块上升到最高点的过程中克服重力做的功不相同 D．两滑块上升到最高点的过程中机械能损失相同 答案：D　解析：两滑块到达B点的动能相同，但速度不同，故A错误；两滑块在斜面上运动时加速度相同，由于初速度不同，故上升的最大高度不同，故B错误；两滑块上升到最高点过程克服重力做功为mgh，由能量守恒定律得Ep＝mgh＋μmgcos θ×，所以mgh＝，故两滑块上升到最高点过程克服重力做的功相同，故C错误；由能量守恒定律得ΔE损＝Wf＝μmgcos θ×＝μmghcot θ＝Ep，故D正确．‎ ‎5．(2018·浙江温州模拟)某工地上，一架起重机将放在地面的一个箱子吊起．箱子在起重机钢绳的作用下由静止开始竖直向上运动，运动过程中箱子的机械能E与其位移x的关系图象如图所示，其中0～x1过程的图线为曲线，x1～x2过程的图线为直线．根据图象可知(　　)‎ A．0～x1过程中钢绳的拉力逐渐增大 B．0～x1过程中箱子的动能一直增加 C．x1～x2过程中钢绳的拉力一直不变 D．x1～x2过程中起重机的输出功率一直增大 答案：C　解析：在Ex图象中，切线的斜率表示拉力，由图可知0～x1过程中拉力逐渐减小，当拉力与重力相等时，重物匀速上升；若拉力小于重力，则减速上升，选项A、B错误；由于x1～x2为直线，所以拉力不变，若匀速上升，则输出功率不变，C正确，D错误．‎ ‎6．如图所示，质量为M的木块静止在光滑的水平面上，质量为m的子弹以速度v0沿水平方向射中木块并最终留在木块中与木块一起以速度v运动．已知当子弹相对木块静止时，木块前进距离L，子弹进入木块的深度为L′，若木块对子弹的阻力F视为恒力，则下列关系式中正确的是(　　)‎ A．FL＝Mv2‎ B．FL′＝mv2‎ C．FL′＝mv－(M＋m)v2‎ D．F(L＋L′)＝mv－mv2‎ 答案：ACD　解析：根据动能定理：对子弹：－F(L＋L′)＝mv2－mv，选项D正确；对木块：FL＝Mv2，A项正确；由以上两式整理可得FL′＝mv－(M＋m)v2，C项正确．‎ ‎7．如图所示，静止放在水平桌面上的纸带，其上有一质量为m＝‎1.0 kg的铁块，它与纸带右端的距离为L＝‎0.5 m，所有接触面之间的动摩擦因数相同．现用水平向左的恒力，经1 s时间将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘且速度为v＝‎2 m/s.已知桌面高度为H＝‎0.8 m，不计纸带重力，铁块可视为质点．重力加速度取g＝‎10 m/s，求：‎ ‎(1)铁块抛出后落地点离抛出点的水平距离；‎ ‎(2)纸带抽出过程中系统产生的内能．‎ 答案：(1)‎0.8 m　(2)4 J 解析：(1)铁块离开桌面后做平抛运动，水平方向：x＝vt1‎ 竖直方向：H＝gt 解得：x＝‎0.8 m.‎ ‎(2)设铁块的加速度为a1，由牛顿第二定律得μmg＝ma1‎ 纸带抽出时，铁块的速度v＝a1t1‎ 联立解得：μ＝0.2‎ 设纸带的位移为x2，铁块的位移：x1＝a1t 由题意知：x2－x1＝L 由功能关系可得系统产生的内能E＝μmgx2＋μmg(x2－x1)‎ 联立解得E＝4 J.‎ ‎[能力提升]‎ ‎8．(2018·河北衡水中学四调)(多选)如图所示，光滑水平面上放着足够长的木板B，木板B上放着木块A，A、B间的接触面粗糙，现在用一水平拉力F作用在A上，使其由静止开始运动，则下列说法正确的是(　　)‎ A．拉力F做的功等于A、B系统动能的增加量 B．拉力F做的功大于A、B系统动能的增加量 C．拉力F和B对A做的功之和小于A的动能的增加量 D．A对B做的功等于B的动能的增加量 答案：BD　解析：对整体分析可知，F做功转化为两个物体的动能及系统的内能，故F做的功一定大于A、B系统动能的增加量，故A错误，B正确；由动能定理可知，拉力F和B对A做的功之和等于A的动能的增加量，选项C错误；根据动能定理可知，A对B做的功等于B的动能的增加量，选项D正确．‎ ‎9. (2018·四川泸州一诊)(多选)如图所示，一个质量为m 的刚性圆环套在粗糙的竖直固定细杆上，圆环的直径略大于细杆的直径，圆环的两边与两个相同的轻质弹簧的一端相连，轻质弹簧的另一端连在和圆环同一高度的墙壁上的P、Q两点处，弹簧的劲度系数为k，起初圆环处于O点，弹簧处于原长状态且弹簧的原长为L.细杆上面的A、B两点到O点的距离都为L.将圆环拉至A点由静止释放，重力加速度为g，对于圆环从A点运动到B点的过程中，下列说法正确的是(　　)‎ A．圆环通过O点的加速度小于g B．圆环在O点的速度最大 C．圆环在A点时的加速度大小为g＋ D．圆环在B点的速度为2 答案：CD　解析：圆环通过O点时只受重力，加速度等于g，由于有加速度，速度继续增加，A、B项错误；圆环在A点时，根据牛顿第二定律mg＋k(L－L)·＝ma，得a＝g＋，C正确；从A到B过程中，由于弹性势能始末状态相等，所以减少的重力势能全部转化为动能，即2mgL＝mv2，所以v＝2，D正确．‎ ‎10．(2018·河南实验中学模拟)(多选)在一水平向右匀速运动的传送带的左端A点，每隔相同的时间T ‎，轻放上一个相同的工件．已知工件与传送带间动摩擦因数为μ，工件质量为m.经测量，发现后面那些已经和传送带达到相同速度的工件之间的距离均为L.已知重力加速度为g，下列判断正确的有(　　)‎ A．传送带的速度大小为 B．工件在传送带上加速时间为 C．每个工件与传送带间因摩擦而产生的热量为 D．传送带因传送每一个工件而多消耗的能量为 答案：AD　解析：工件在传送带上先做匀加速直线运动，然后做匀速直线运动，每个工件滑上传送带后运动的规律相同，可知L＝vT，解得传送带的速度v＝，故A正确．设每个工件匀加速运动的时间为t，根据牛顿第二定律得，工件的加速度为μg，根据v＝v0＋at，解得：t＝＝，故B错误．工件与传送带相对滑动的路程为：Δx＝v－＝＝，则摩擦产生的热量为：Q＝μmgΔx＝，故C错误．根据能量守恒得，传送带因传送一个工件多消耗的能量E＝mv2＋μmgΔx＝，故D正确．‎ ‎11．(多选)如图甲所示，竖直光滑杆固定不动，弹簧下端固定，将滑块向下压缩弹簧至离地高度h＝‎‎0.1 m 处，滑块与弹簧不拴接．现由静止释放滑块，通过传感器测量到滑块的速度和离地高度h，并作出其Ekh图象，如图乙所示，其中高度从‎0.2 m上升到‎0.35 m范围内图象为直线，其余部分为曲线．以地面为零势能面，取g＝‎10 m/s2，由图象可知(　　)‎ 甲 ‎　‎ 乙 A．轻弹簧原长为‎0.2 m B．滑块的质量为‎0.1 kg C．弹簧最大弹性势能为0.5 J D．滑块的重力势能与弹簧的弹性势能之和最小时，动能为0.3 J 答案：AC　解析：因为从‎0.2 m开始为直线，说明只有重力做负功，弹簧恢复原长，A项正确；由动能定理：－mgh′＝0－Ek(h′为直线对应高度)，m＝＝ kg＝‎0.2 kg，B项错误；弹簧的弹性势能最终全部转化为重力势能，Ep＝mgh″‎ ‎＝0.2×10×(0.35－0.1) J＝0.5 J，C项正确；重力势能与弹性势能之和最小时，应是动能最大时，从题图可得最大动能为Ek＝0.32 J，D项错误．‎ ‎12．(2018·江苏泰州中学期中)如图所示，传送带AB总长为l＝‎10 m，与一个半径为R＝‎0.4 m的光滑四分之一圆轨道BC相切于B点，传送带速度恒为v＝‎6 m/s，方向向右，现有一个滑块以一定初速度从A点水平滑上传送带，滑块质量为m＝‎10 kg，滑块与传送带间的动摩擦因数为μ＝0.1，已知滑块运动到B端时，刚好与传送带同速，求：‎ ‎(1)滑块的初速度；‎ ‎(2)滑块能上升的最大高度；‎ ‎(3)求滑块第二次在传送带上滑行时，滑块和传送带系统产生的内能．‎ 答案：(1)‎2 m/s或‎4 m/s　(2)‎1.8 m　(3)220 J 解析：(1)以滑块为研究对象，滑块在传送带上运动过程中，当滑块初速度大于传送带速度时，有－μmgl＝mv2－mv，解得v0＝‎2 m/s；‎ 当滑块初速度小于传送带速度时，有μmgl＝mv2－mv，解得v0＝‎4 m/s.‎ ‎(2)由动能定理可得－mgh＝0－mv2，解得h＝‎1.8 m.‎ ‎(3)以滑块为研究对象，由牛顿第二定律得μmg＝ma ‎，滑块的加速度a＝‎1 m/s2，滑块减速到零的位移s＝＝‎18 m>‎10 m，则滑块第二次在传送带上滑行时，速度没有减小到零就离开传送带，由匀变速运动的位移公式可得l＝vt－at2，解得t＝2 s(t＝10 s舍去)，在此时间内传送带的位移x＝vt＝6×‎2 m＝‎12 m，滑块第二次在传送带上滑行时，滑块和传送带系统产生的内能 Q＝μmg(l＋x)＝0.1×10×10×(10＋12) J＝220 J.‎