- 2021-05-22 发布 |
- 37.5 KB |
- 6页

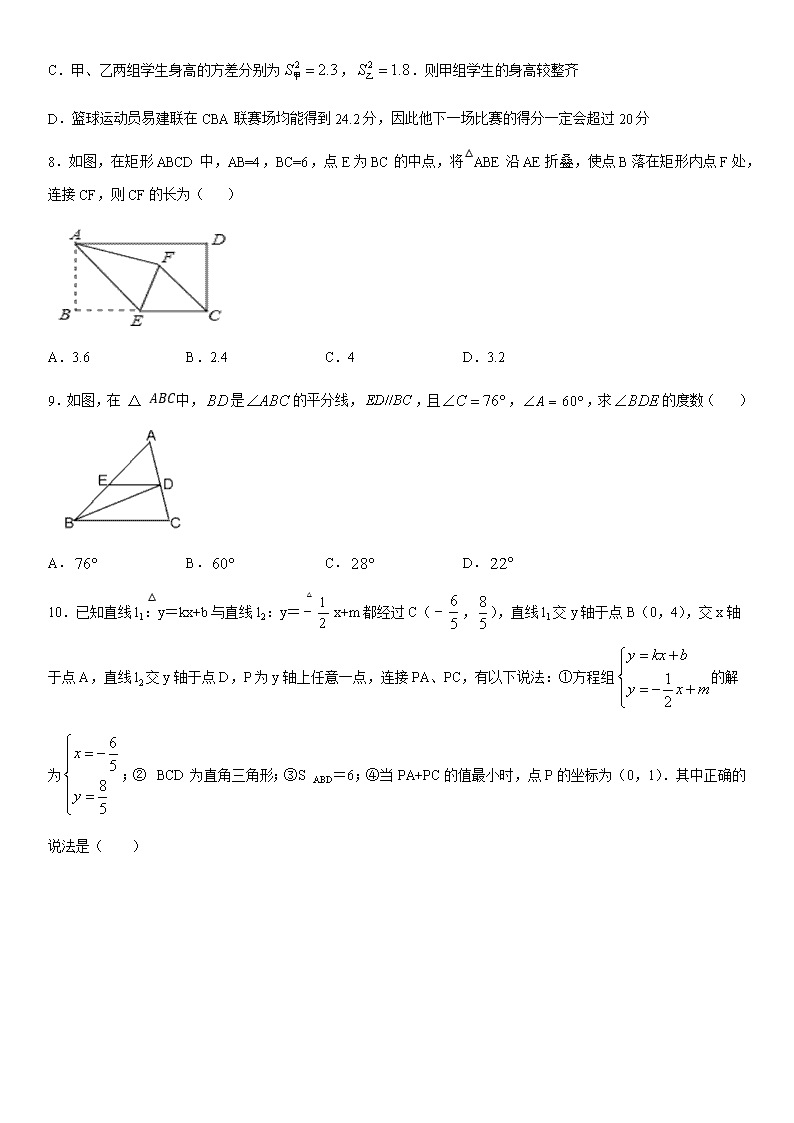
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版八年级数学上册数学期末综合测试(一)
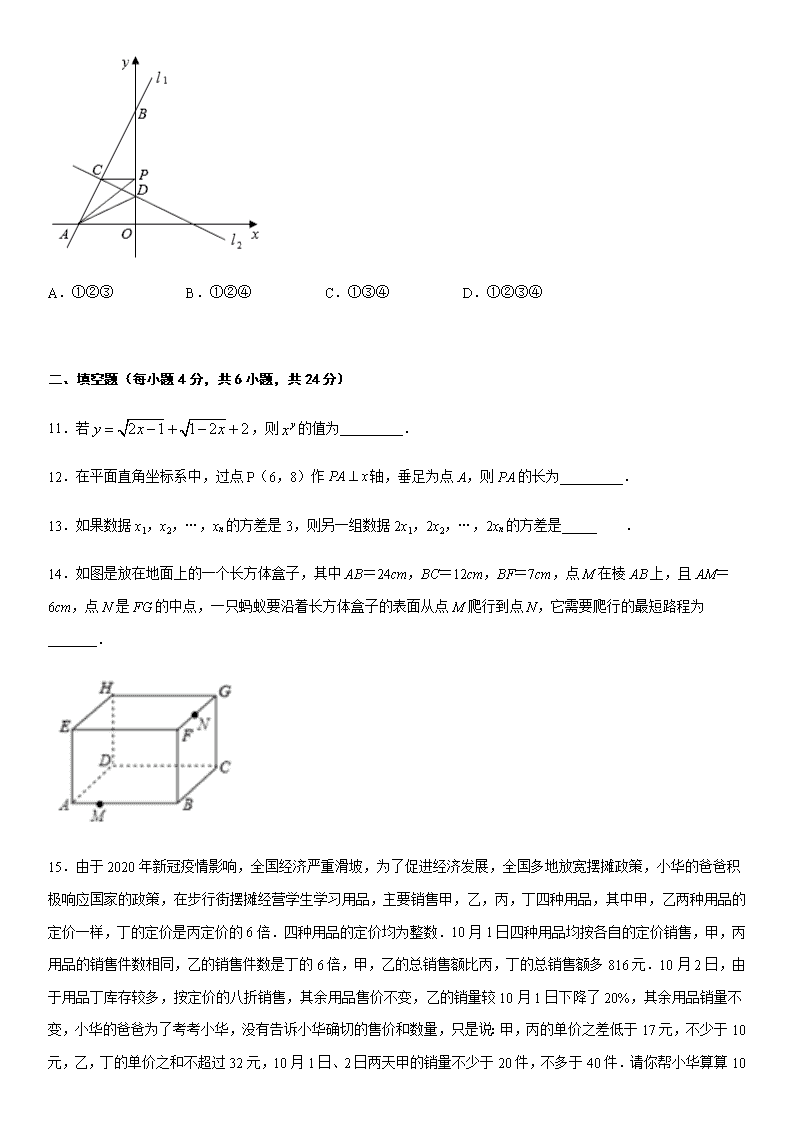
北师大版八年级数学上学期数学期末综合测试(一) 一、选择题(每小题 3 分,有 10 小题,共 30 分) 1.点 P(3, 4 )关于 x 轴对称的点的坐标是( ) A.(3, 4 ) B.( 3 , 4 ) C.(3,4) D.( 3 ,4) 2.在 1 7 ,0, 7 ,-7 这四个数中,为无理数的是( ) A.0 B. 1 7 C. 7 D.-7 3.下列说法中:①每个正数都有两个立方根;②平方根是它本身的数有 1,0;③立方根是它本身的数有±1,0;④ 如果一个数的平方根等于它的立方根,那么这个数是 1 或 0;⑤没有平方根的数也没有立方根;⑥算术平方根是它 本身的数有 1,0.其中正确的有( ) A.2 个 B.3 个 C.4 个 D.5 个 4.下列根式是最简二次根式的是( ) A. 0.6 B. 6 C. 16 D. 1 6 5.下列各曲线中,不表示 y 是 x 的函数的是( ) A. B. C. D. 6.对每个 x 的值,y 是 1 2y x , 2 2y x , 3y x 中的最大值,则当 x 变化时,函数 y 的最小值为( ) A.1 B.4 C.8 D. 48 7 7.下列说法正确的是( ) A.北斗系统第五十五颗导航卫星发射前的零件检查,应选择抽样调查 B.一组数据 6,5,8,8,9 的众数是 8 C.甲、乙两组学生身高的方差分别为 2 2.3S 甲 , 2 1.8S 乙 .则甲组学生的身高较整齐 D.篮球运动员易建联在 CBA 联赛场均能得到 24.2 分,因此他下一场比赛的得分一定会超过 20 分 8.如图,在矩形 ABCD 中,AB=4,BC=6,点 E 为 BC 的中点,将 △ ABE 沿 AE 折叠,使点 B 落在矩形内点 F 处, 连接 CF,则 CF 的长为( ) A.3.6 B.2.4 C.4 D.3.2 9.如图,在△ �an 中, BD 是 ABC 的平分线, //ED BC ,且 76C , 60A ,求 BDE 的度数( ) A. 76 B. 60 C. 28 D. 22 10.已知直线 l1:y=kx+b 与直线 l2:y=﹣ 1 2 x+m 都经过 C(﹣ 6 5 , 8 5 ),直线 l1 交 y 轴于点 B(0,4),交 x 轴 于点 A,直线 l2 交 y 轴于点 D,P 为 y 轴上任意一点,连接 PA、PC,有以下说法:①方程组 1 2 y kx b y x m 的解为 6 5 8 5 x y ;② △ BCD 为直角三角形;③S △ ABD=6;④当 PA+PC 的值最小时,点 P 的坐标为(0,1).其中正确的说 法是( ) A.①②③ B.①②④ C.①③④ D.①②③④ 二、填空题(每小题 4 分,共 6 小题,共 24 分) 11.若 2 1 1 2 2y x x ,则 yx 的值为_________. 12.在平面直角坐标系中,过点 P(6,8)作 PA x 轴,垂足为点 A,则 PA 的长为_________. 13.如果数据 x1,x2,…,xn 的方差是 3,则另一组数据 2x1,2x2,…,2xn 的方差是_____ . 14.如图是放在地面上的一个长方体盒子,其中 AB=24cm,BC=12cm,BF=7cm,点 M 在棱 AB 上,且 AM=6cm, 点 N 是 FG 的中点,一只蚂蚁要沿着长方体盒子的表面从点 M 爬行到点 N,它需要爬行的最短路程为_______. 15.由于 2020 年新冠疫情影响,全国经济严重滑坡,为了促进经济发展,全国多地放宽摆摊政策,小华的爸爸积 极响应国家的政策,在步行街摆摊经营学生学习用品,主要销售甲,乙,丙,丁四种用品,其中甲,乙两种用品的 定价一样,丁的定价是丙定价的 6 倍.四种用品的定价均为整数.10 月 1 日四种用品均按各自的定价销售,甲,丙 用品的销售件数相同,乙的销售件数是丁的 6 倍,甲,乙的总销售额比丙,丁的总销售额多 816 元.10 月 2 日,由 于用品丁库存较多,按定价的八折销售,其余用品售价不变,乙的销量较 10 月 1 日下降了 20%,其余用品销量不 变,小华的爸爸为了考考小华,没有告诉小华确切的售价和数量,只是说:甲,丙的单价之差低于 17 元,不少于 10 元,乙,丁的单价之和不超过 32 元,10 月 1 日、2 日两天甲的销量不少于 20 件,不多于 40 件.请你帮小华算 算 10 月 2 日甲,乙,丙,丁,四种用品的销售额最多_____元. 16.△ �an 中, �a��n 边上的高 nܧ�a� 相交于点 F,∠ �an� ∠ �na 的角平分线交于点 G,若 =125CGB ,则 CFB ______. 三、解答题(共 7 小题,共 66 分) 17.(本题 6)计算: 12 1 33 1 8 6 3 2 . 18.(本题 8 分)按要求作图并填空: (1)作出△ �an 关于 x 轴对称的△ � � a � n � ; (2)作出过点 1,0 且平行于 y 轴的直线l ,则点 ,P a b 关于直线l 的对称点 P 的坐标为______. (3)在 x 轴上画出点Q ,使QA QC 最小. 19.(本题 8 分)某酒厂生产 A 、 B 两种品牌的酒,每天两种酒共生产 600 瓶,每种酒每瓶的成本和利润如下表所 示. 设每天共获利 y 元,每天生产 A 种品牌的酒 x 瓶. A B 成本(元) 50 35 利润(元) 20 15 (1)请写出 y 关于 x 的函数关系式; (2)如果该厂每天至少投入成本 25000 元,且生产 B 种品牌的酒不少于全天产量的 55%,那么共有几种生产方案? 并求出每天至少获利多少元? 20.(本题 10 分)某校举行了主题为“新冠肺炎防护”的知识竞赛活动,对八年级的两班学生进行了预选,其中各 班前 5 名学生的成绩(百分制,单位:分)分别为:八(1)班 86,85,77,92,85;八(2)班 79,85,92,85, 89.通过数据分析,列表如下: 班级 平均分 中位数 众数 方差 八(1) 85 a b 22.8 八(2) 86 85 85 19.2 (1)直接写出表中 ,a b 的值: a ______,b ______. (2)根据以上数据分析,你认为哪个班前 5 名同学的成绩较好?说明理由. 21.(本题 10 分)如图,已知 1 2 , C D ,求证: A F . 22.(本题 12 分)已知,在等腰直角△ �an 中, AB AC , 90BAC ,点 D 是 AC 边上一点,以 BD 为边作 等腰直角△ a�ܧ ,其中 BD BE , 90DBE ,边 AB 与 D 交于点 F,点 G 是 BC 上一点. (1)如图 1,若 DG DE ,连接 FG . ①若 30ABD , 6 2DE ,求 BF 的长. ②求证: DG EF FG . (2)如图 2,若 DG BD , EP BE 交 BA 的延长线于点 P ,连接 PG ,请猜想线段 PG , DG , PE 的之间 数量关系,并证明. (3)在(2)的条件下, 37BG , 1DG , 7GP ,点 H 为线段 AC 上一点,一动点 M 从点 G 出发,以每 秒 1 个单位的速度沿线段GH 运动,再以每秒 2 个单位的速度延折线 H-A-P 运动到 P 点后停止,求点 M 在整 个运动过程中用时最少为多少秒? 23.(本题 12 分)如图,直线 y kx b 与 x 轴、y 轴分别交于点 4,0A 、 0,4B ,点 P 在 x 轴上运动,连接 PB , 将△ �ah 沿直线 BP 折叠,点O 的对应点记为 O . (1)求 k 、b 的值. (2)在 x 轴上是否存在点C ,使得△ �an 为等腰三角形?若存在,求出点C 的坐标,若不存在,说明理由. (3)若点 O 恰好落在直线 AB 上,求△ �ah 的面积.查看更多