- 2021-05-22 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学同步练习4-3 第1课时 利用“边边边”判定三角形全等 北师大版
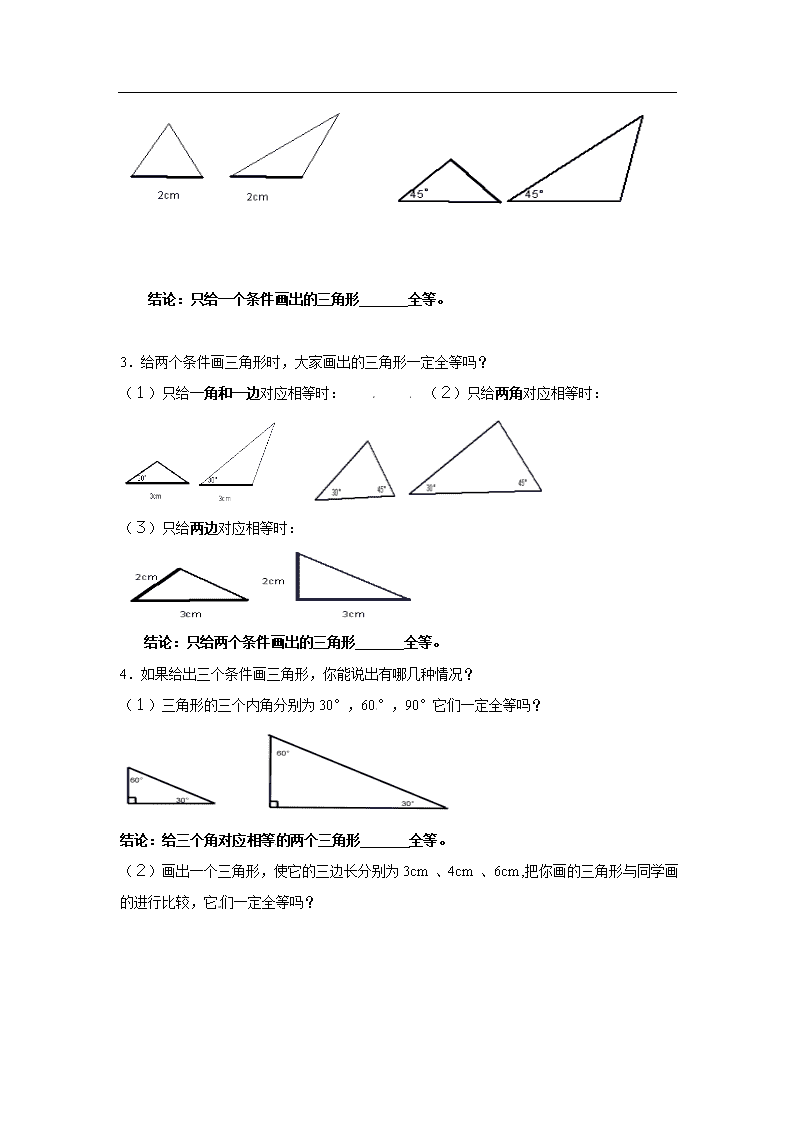
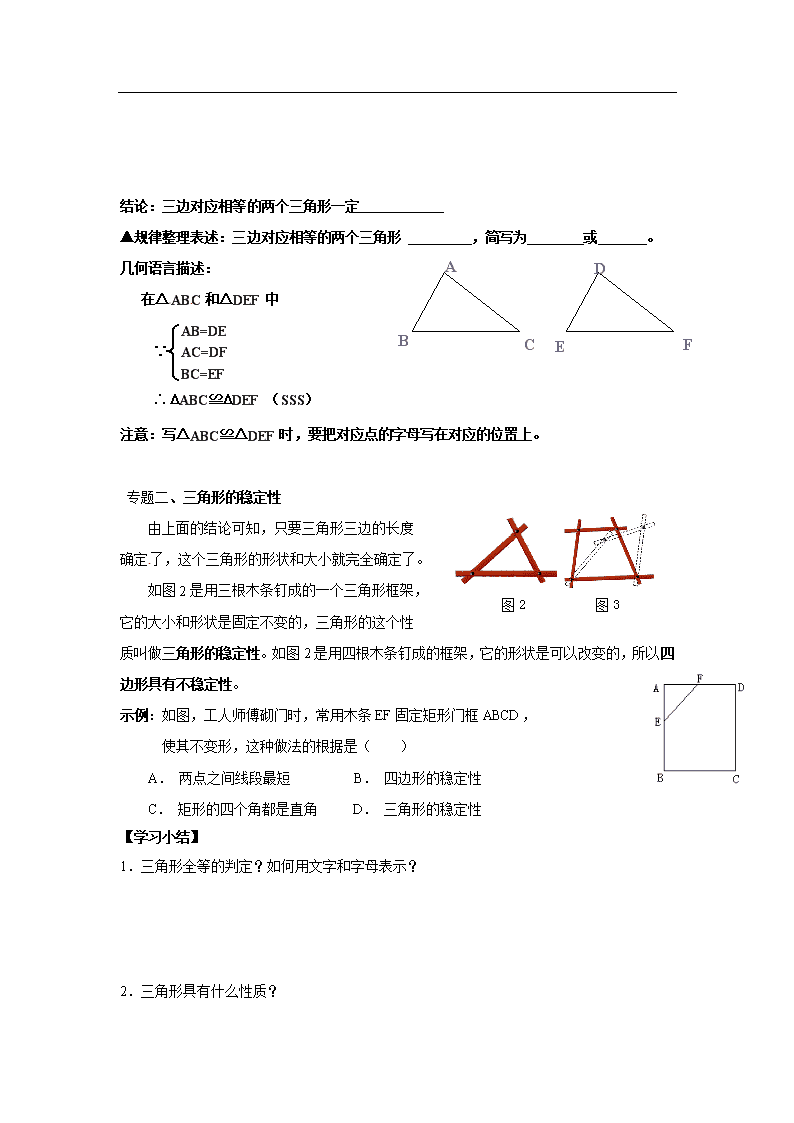
4.3 第1课时 利用“边边边”判定三角形全等 【学习目标】 1.掌握三角形全等“边边边”条件,了解三角形的稳定性; 2.在探索三角形全等条件及其运用的过程中,能够进行简单的推理。 【使用说明与学法指导】 1.先精读一遍教材P97-P99页,在探索三角形全等条件及其运用的过程中,能够进行简单的推理。 针对课前预习二次阅读教材,并回答问题. 2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑. 【课前预习】 一、知识引入 1. 两个三角形,称为全等三角形。全等三角形的 相等, 相等。 2.如图1,已知△AOC≌△BOD,则∠A=∠B,∠C= , =∠2,对应边有AC= , =OB, =OD。 1. 自主预习书本P97-P99页.[来源:Z+xx+k.Com] 【课堂探究】 专题一、探索三角形全等的条件 1.思考:三角形中一共六个元素,三条边和三个角。如果对应边和对应角都相等的话,那么三角形肯定全等。要画一个三角形与已知的三角形全等,条件能否尽可能少吗?一个条件行吗?两个条件、三个条件呢? 2.只给一个条件画三角形时,大家画出的三角形一定全等吗? (1)只给一条边对应相等时 : (2) 只给一个角对应相等时: 结论:只给一个条件画出的三角形 全等。 3.给两个条件画三角形时,大家画出的三角形一定全等吗? (1)只给一角和一边对应相等时: (2)只给两角对应相等时: (3)只给两边对应相等时: 结论:只给两个条件画出的三角形 全等。[来源:学*科*网Z*X*X*K] 4.如果给出三个条件画三角形,你能说出有哪几种情况? (1)三角形的三个内角分别为30°,60°,90°它们一定全等吗? 结论:给三个角对应相等的两个三角形 全等。 (2)画出一个三角形,使它的三边长分别为3cm 、4cm 、6cm ,把你画的三角形与同学画的进行比较,它们一定全等吗? 结论:三边对应相等的两个三角形一定 ▲规律整理表述:三边对应相等的两个三角形 ,简写为 或 。 B C E F D A 几何语言描述: 在△ABC和△DEF中 ∴ DABC≌DDEF (SSS) AB=DE ∵ AC=DF BC=EF 注意:写△ABC≌△DEF时,要把对应点的字母写在对应的位置上。 专题二、三角形的稳定性 由上面的结论可知,只要三角形三边的长度 确定了,这个三角形的形状和大小就完全确定了。 图2 图3 如图2是用三根木条钉成的一个三角形框架, 它的大小和形状是固定不变的,三角形的这个性 质叫做三角形的稳定性。如图2是用四根木条钉成的框架,它的形状是可以改变的,所以四边形具有不稳定性。 示例:如图,工人师傅砌门时,常用木条EF固定矩形门框ABCD, 使其不变形,这种做法的根据是( ) A. 两点之间线段最短 B. 四边形的稳定性 C. 矩形的四个角都是直角 D. 三角形的稳定性 【学习小结】 1.三角形全等的判定?如何用文字和字母表示? 2.三角形具有什么性质? [来源:Zxxk.Com] 【课堂检测】 1.1976年7月28日,我国河北唐山市发生了里氏7.8级地震,房屋大部分倒塌,事后 发现,房屋破坏最轻的是那些有三角形房顶的木结构房子,如图1所示,请问这是 的作用。 ★2. 如图2,已知AC=AD,BC=BD,CE=DE,则全等三角形共有 对。 图1 图3 图2 ★★3.如图,在△ABC中,AB=AC,D是BC的中点,∠B=∠C 吗?你能说明理由吗? [来源:学|科|网Z|X|X|K] 【巩固作业】 1.看图填空:已知:如图,AC=DF,BC=EF,AD=BE,试说明: BC∥ EF, AC∥DF。 解:∵AD=BE ( ) C F A D B E ∴________=BE+DB(等量加等量和相等)即:________=________ 在△ABC和△DEF中 ________________( ) ________________( ) ________________( ) ∴△ABC ≌ △DEF( ) ∴______=______, ______=______( ) ∴______∥______ , ______∥______( ) 2.如图,A、C、F、P在同一直线上,AF=PC,AB=PE,BC=EF。 你能找到哪两个三角形全等?并说明理由。 ★3.如图,已知,,试说明:。 ★★4.如图,已知DB =CA,请增加一个条件,使△ABC≌△BAD,则需要增加的条件是________________,并说明全等的理由。 [来源:学#科#网]查看更多