全国(甲卷、乙卷、丙卷)高考数学试题，高分必备

全国(甲卷、乙卷、丙卷)高考数学试题，高分必备

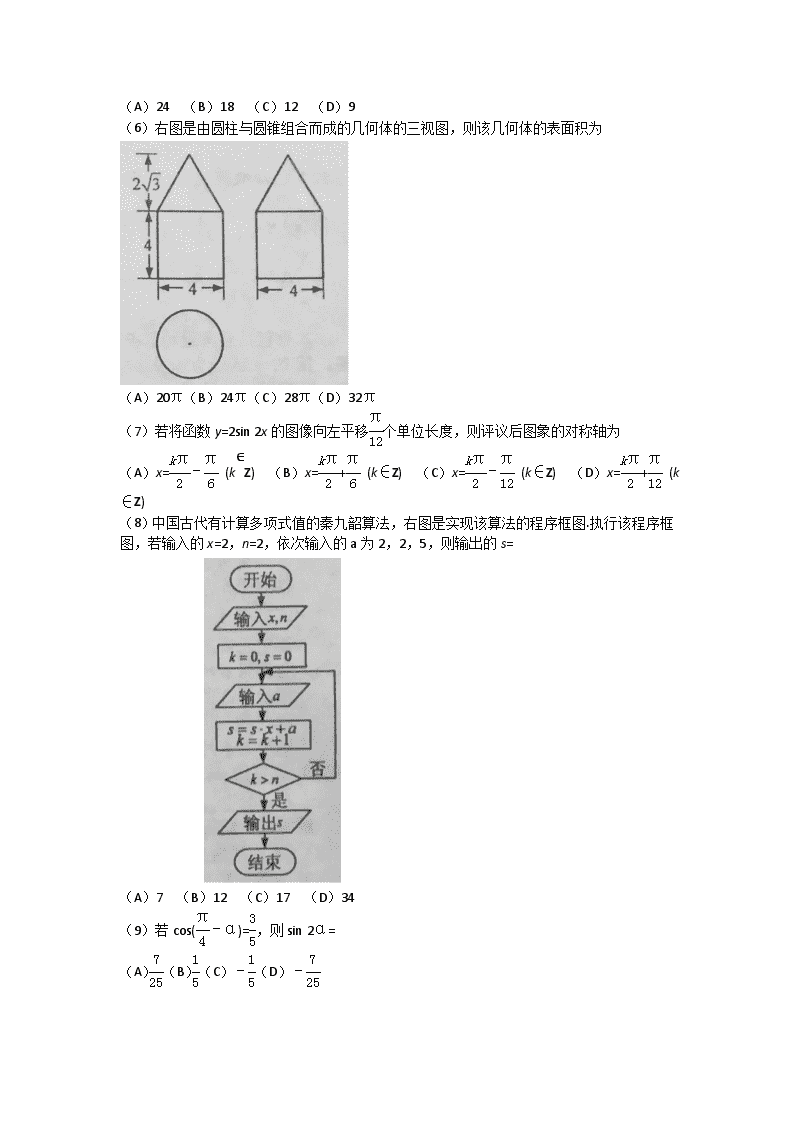
全国(甲卷、乙卷、丙卷)高考数学试题，高分必备 2016 年普通高等学校招生全国统一考试附参考答案和解析 理科数学 注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷 1 至 3 页，第Ⅱ卷 3 至 5 页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回. 第Ⅰ卷 一. 选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只 有一项是符合题目要求的. （1）已知 ( 3) ( 1)iz m m    在复平面内对应的点在第四象限，则实数 m 的取值范 围是 （A） ( 31) ， （B） ( 1 3) ， （C） (1, )+ （D） ( 3) - ， （2）已知集合 {1, }A  2,3 ， { | ( 1)( 2) 0, }B x x x x    Z ，则 A B  （A）{1}（B）{1 2}， （C）{01 2 3}，，， （D）{ 1 01 2 3} ，，，， （3）已知向量 (1, ) (3, 2)m ， =a b ，且 ( ) a + b b ，则 m= （A）－8（B）－6 （C）6 （D）8 （4）圆 2 2 2 8 13 0x y x y     的圆心到直线 1 0ax y   的距离为 1，则 a= （A） 4 3  （B） 3 4  （C） 3 （D）2 （5）如图，小明从街道的 E 处出发，先到 F 处与小红会合，再一起到位于 G 处的老年 公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为 （A）24 （B）18 （C）12 （D）9 （6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为 （A）20π（B）24π（C）28π（D）32π （7）若将函数 y=2sin 2x 的图像向左平移π 12 个单位长度，则评议后图象的对称轴为 （A）x=kπ 2 –π 6 (k∈Z) （B）x=kπ 2 +π 6 (k∈Z) （C）x=kπ 2 –π 12 (k∈Z) （D）x=kπ 2 +π 12 (k ∈Z) （8）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框 图，若输入的 x=2，n=2，依次输入的 a 为 2，2，5，则输出的 s= （A）7 （B）12 （C）17 （D）34 （9）若 cos(π 4 –α)=3 5 ，则 sin 2α= （A）7 25 （B）1 5 （C）–1 5 （D）– 7 25 （10）从区间 0,1 随机抽取 2n 个数 1x , 2x ，…， nx ， 1y ， 2y ，…， ny ，构成 n 个数对 1 1,x y ，  2 2,x y ，…， ,n nx y ，其中两数的平方和小于 1 的数对共有 m 个，则用随机模拟的方法 得到的圆周率 的近似值为 （A） 4n m （B） 2n m （C） 4m n （D） 2m n （11）已知 F1，F2 是双曲线 E 2 2 2 2 1x y a b   的左，右焦点，点 M 在 E 上，M F1 与 x 轴垂 直，sin 2 1 1 3MF F  ,则 E 的离心率为 （A） 2 （B） 3 2 （C） 3 （D）2 （12）已知函数 ( )( )f x xR 满足 ( ) 2 ( )f x f x   ，若函数 1xy x  与 ( )y f x 图 像的交点为 1 1 2 2( , ),( , ), ,( , ),m mx y x y x y 则 1 ( ) m i i i x y    （A）0 （B）m（C）2m（D）4m 第 II 卷 本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都 必须作答.第(22)题~第(24)题为选考题，考生根据要求作答. 二、填空题：本大题共 3 小题，每小题 5 分 (13)△ABC 的内角 A、B、C 的对边分别为 a、b、c，若 cos A= 4 5 ，cos C= 5 13 ，a=1，则 b=. (14)α、β是两个平面，m、n 是两条直线，有下列四个命题： （1）如果 m⊥n，m⊥α，n∥β，那么α⊥β. （2）如果 m⊥α，n∥α，那么 m⊥n. （3）如果α∥β，m α，那么 m∥β. （4）如果 m∥n，α∥β，那么 m 与α所成的角和 n 与β所成的角相等. 其中正确的命题有.(填写所有正确命题的编号） （15）有三张卡片，分别写有 1 和 2，1 和 3，2 和 3。甲，乙，丙三人各取走一张卡片，甲 看了乙的卡片后说：“我与乙的卡片上相同的数字不是 2”，乙看了丙的卡片后说：“我与丙 的卡片上相同的数字不是 1”，丙说：“我的卡片上的数字之和不是 5”，则甲的卡片上的数字 是。 （16）若直线 y=kx+b 是曲线 y=lnx+2 的切线，也是曲线 y=ln（x+2）的切线，则 b=。 三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本题满分 12 分） nS 为等差数列 na 的前 n 项和，且 7=1 28.na S ， 记  = lgn nb a ，其中 x 表示不超过 x 的最大整数，如   0.9 =0 lg99 =1， . （I）求 1 11 101b b b， ， ； （II）求数列 nb 的前 1 000 项和. 18.（本题满分 12 分） 某险种的基本保费为 a（单位：元），继续购买该险种的投保人称为续保人，续保人的本年 度的保费与其上年度的出险次数的关联如下： 上 年 度 出 险次数 0 1 2 3 4  5 保费 0.85a a 1.25a 1.5a 1.75a 2a 设该险种一续保人一年内出险次数与相应概率如下： 一 年 内 出 险次数 0 1 2 3 4  5 概率 0.30 0.15 0.20 0.20 0.10 0. 05 （I）求一续保人本年度的保费高于基本保费的概率； （II）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出 60%的概率； （III）求续保人本年度的平均保费与基本保费的比值. 19.（本小题满分 12 分） 如图，菱形 ABCD 的对角线 AC 与 BD 交于点 O，AB=5，AC=6，点 E,F 分别在 AD,CD 上，AE=CF= 5 4 ， EF 交 BD 于点 H.将△DEF 沿 EF 折到△ D EF 的位置， 10OD  . （I）证明： D H 平面 ABCD； （II）求二面角 B D A C  的正弦值. 20.（本小题满分 12 分） 已知椭圆 E: 2 2 13 x y t   的焦点在 x 轴上，A 是 E 的左顶点，斜率为 k(k>0)的直线交 E 于 A,M 两点，点 N 在 E 上，MA⊥NA. （I）当 t=4， AM AN 时，求△AMN 的面积； （II）当 2 AM AN 时，求 k 的取值范围. （21）（本小题满分 12 分） (I)讨论函数 xx 2f (x) x 2   e 的单调性，并证明当 x >0 时， ( 2) 2 0;xx e x    (II)证明：当 [0,1)a 时，函数 2x = ( 0) xe ax ag xx   （ ） 有最小值.设 g（x）的最小值为 ( )h a ， 求函数 ( )h a 的值域. 请考生在 22、23、24 题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题 号 （22）（本小题满分 10 分）选修 4-1：集合证明选讲 如图，在正方形 ABCD，E,G 分别在边 DA,DC 上（不与端点重合），且 DE=DG，过 D 点作 DF ⊥CE，垂足为 F. (I) 证明：B,C,E,F 四点共圆； (II)若 AB=1，E 为 DA 的中点，求四边形 BCGF 的面积. （23）（本小题满分 10 分）选修 4—4：坐标系与参数方程 在直线坐标系 xoy 中，圆 C 的方程为（x+6）2+y2=25. （I）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求 C 的极坐标方程； （II）直线 l 的参数方程是 （t 为参数）,l 与 C 交于 A、B 两点，∣AB∣= ， 求 l 的斜率。 （24）（本小题满分 10 分），选修 4—5：不等式选讲 已知函数 f(x)= ∣x- ∣+∣x+ ∣，M 为不等式 f(x)＜2 的解集. （I）求 M； （II）证明：当 a,b∈M 时，∣a+b∣＜∣1+ab∣。 2016 年普通高等学校招生全国统一考试附参考答案和解析 理科数学 1-12：ACDAB,CBCDC,AB 13：21/13 14：2，3，4 15：1 和 3 16:1-ln2 2016 年普通高等学校招生全国统一考试附参考答案和解析 文科数学 注意事项： 1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的 姓名、准考证号填写在本试卷和答题卡相应位置上。 2．回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号框涂黑，如 需改动，用橡皮擦干净后，再选涂其他答案标号框。写在本试卷上无效。 3．答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。 4．考试结束，将试题卷和答题卡一并交回。 第Ⅰ卷 一、 选择题：本大题共 12 小题。每小题 5 分，在每个小题给出的四个选项中，只有一项是 符合要求的。 （1）已知集合 {12 3}A  ，，， 2{ | 9}B x x  ，则 A B  （A）{ 2 1 0 1 2 3} ， ，，，， （B）{ 2 1 0 1 2} ， ，，， （C）{1 2 3}，， （D）{1 2}， （2）设复数 z 满足 i 3 iz    ，则 z = （A） 1 2i  （B）1 2i （C）3 2i （D）3-2i (3) 函数 = sin( )y A x  的部分图像如图所示，则 （A） 2sin(2 )6y x   （B） 2sin(2 )3y x   （C） （D） (4) 体积为 8 的正方体的顶点都在同一球面上，则该球面的表面积为 （A）12 （B） 32 3  （C）（D）  (5) 设 F 为抛物线 C：y2=4x 的焦点，曲线 y= k x （k>0）与 C 交于点 P，PF⊥x 轴，则 k= （A） 1 2 （B）1 （C） 3 2 （D）2 (6) 圆 x2+y2−2x−8y+13=0 的圆心到直线 ax+y−1=0 的距离为 1，则 a= （A）− 4 3 （B）− 3 4 （C） 3 （D）2 (7) 如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为 （A）20π（B）24π（C）28π（D）32π (8) 某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为 40 秒.若一名行 人来到该路口遇到红灯，则至少需要等待 15 秒才出现绿灯的概率为 （A） 7 10 （B） 5 8 （C） 3 8 （D） 3 10 (9)中国古代有计算多项式值得的秦九韶算法，右图是实现该算法的程序框图．执行该 程序框图，若输入的 x=2，n=2，依闪输入的 a 为 2，2，5，则输出的 s= （A）7 （B）12 （C）17 （D）34 (10) 下列函数中，其定义域和值域分别与函数 y=10lgx 的定义域和值域相同的是 （A）y=x（B）y=lgx（C）y=2x（D） 1y x  (11) 函数 π( ) cos2 6cos( )2f x x x   的最大值为 （A）4（B）5 （C）6 （D）7 (12) 已知函数 f(x)（x∈R）满足 f(x)=f(2-x)，若函数 y=|x2-2x-3| 与 y=f(x) 图像的交点为（x1,y1）， (x2,y2)，…，（xm,ym），则 1 = m i i x   (A)0 (B)m (C) 2m (D) 4m 第Ⅱ卷 本卷包括必考题和选考题两部分。第 13~21 题为必考题，每个试题考生都必须作答。第 22～ 24 题为选考题，考生根据要求作答。 二、填空题：共 4 小题，每小题 5 分. (13) 已知向量 a=(m,4)，b=(3,-2)，且 a∥b，则 m=___________. (14) 若 x，y 满足约束条件 1 0 3 0 3 0 x y x y x           ，则 z=x-2y 的最小值为__________ （15）△ABC 的内角 A，B，C 的对边分别为 a，b，c，若 4cos 5A  ， 5cos 13C  ，a=1，则 b=____________. （16）有三张卡片，分别写有 1 和 2，1 和 3，2 和 3. 甲，乙，丙三 人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的 数字不是 2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不 是 1”，丙说：“我的卡片上的数字之和不是 5”，则甲的卡片上的数字 是________________. 三、解答题：解答应写出文字说明，证明过程或演算步骤． （17）(本小题满分 12 分) 等差数列{ na }中， 3 4 5 74, 6a a a a    （I）求{ na }的通项公式； (II)设 nb =[ na ]，求数列{ nb }的前 10 项和，其中[x]表示不超过 x 的最大整数，如 [0.9]=0,[2.6]=2. （18）(本小题满分 12 分) 某险种的基本保费为 a（单位：元），继续购买该险种的投保人称为续保人，续保人本 年度的保费与其上年度出险次数的关联如下： 随机调查了该险种的 200 名续保人在一年内的出险情况，得到如下统计表： （I）记 A 为事件：“一续保人本年度的保费不高于基本保费”。求 P(A)的估计值； (II)记 B 为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的 160％”. 求 P(B)的估计值； （III）求续保人本年度平均保费估计值. （19）（本小题满分 12 分） 如图，菱形 ABCD 的对角线 AC 与 BD 交于点 O，点 E,F 分别在 AD，CD 上，AE=CF，EF 交 BD 于点 H，将△DEF 沿 EF 折到△D′EF 的位置. （I）证明： 'AC HD ； (II)若 55, 6, , ' 2 24AB AC AE OD    ,求五棱锥的 D′-ABCFE 体积. （20）（本小题满分 12 分） 已知函数 ( ) ( 1)ln ( 1)f x x x a x    . （I）当 4a  时，求曲线 ( )y f x 在 1, (1)f 处的切线方程； (II)若当  1,x  时， ( ) 0f x ＞ ，求 a 的取值范围. （21）（本小题满分 12 分） 已知 A 是椭圆 E： 2 2 14 3 x y  的左顶点，斜率为  0k k＞ 的直线交 E 与 A，M 两点，点 N 在 E 上， MA NA . （I）当 AM AN 时，求 AMN 的面积 (II)当 2 AM AN 时，证明： 3 2k  . 请考生在第 22~24 题中任选一题作答，如果多做，则按所做的第一题计分. （22）（本小题满分 10 分）选修 4-1：几何证明选讲 如图，在正方形 ABCD 中，E，G 分别在边 DA，DC 上（不与端点重合）， 且 DE=DG，过 D 点作 DF⊥CE，垂足为 F. （Ⅰ）证明：B，C，G，F 四点共圆； （Ⅱ）若 AB=1，E 为 DA 的中点，求四边形 BCGF 的面积. （23）（本小题满分 10 分）选修 4-4：坐标系与参数方程 在直角坐标系 xOy 中，圆 C 的方程为 2 2( + 6) + = 25x y . （Ⅰ）以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，求 C 的极坐标方程； （Ⅱ）直线 l 的参数方程是 （t 为参数），l 与 C 交于 A，B 两点， 10AB = , 求 l 的斜率. （24）（本小题满分 10 分）选修 4-5：不等式选讲 已知函数 1 1( ) 2 2f x x x= - + + ，M 为不等式 ( ) 2f x < 的解集. （Ⅰ）求 M； （Ⅱ）证明：当 a，b M 时， 1a b ab+ < + . 2016 年普通高等学校招生全国统一考试附参考答案和解析 文科数学 1-12：DCAAD,ACBCD,BB 13:-6 14:-5 15:21/13 16:1 和 3 绝密★启封并使用完毕前 试题类型：A 2016 年普通高等学校招生全国统一考试附参考答案和解析 理科数学 注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷 1 至 3 页，第Ⅱ卷 3 至 5 页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回. 第Ⅰ卷 二. 选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符 合题目要求的. （1）设集合 2{ | 4 3 0}A x x x    ， { | 2 3 0}B x x   ，则 A B  （A） 3( 3, )2   （B） 3( 3, )2  （C） 3(1, )2 （D） 3( ,3)2 （2）设 (1 i) 1 ix y   ，其中 x，y 是实数，则 i =x y （A）1（B） 2 （C） 3 （D）2 （3）已知等差数列{ }na 前 9 项的和为 27， 10 =8a ，则 100 =a （A）100（B）99（C）98（D）97 （4）某公司的班车在 7:00，8:00，8:30 发车，小明在 7:50 至 8:30 之间到达发车站乘坐班 车，且到达发车站的时刻是随机的，则他等车时间不超过 10 分钟的概率是 （A）（B）（C）（D） （5）已知方程–=1 表示双曲线，且该双曲线两焦点间的距离为 4，则 n 的取值范围是 （A）(–1,3) （B）(–1, 3) （C）(0,3) （D）(0, 3) （6）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几 何体的体积是，则它的表面积是 （A）17π（B）18π（C）20π（D）28π （7）函数 y=2x2–e|x|在[–2,2]的图像大致为 （A） （B） （C） （D） （8）若 10 1a b c   ， ，则 （A） c ca b （B） c cab ba （C） log logb aa c b c （D） log loga bc c （9）执行右面的程序图，如果输入的 0 1 1x y n  ， ， ，则输出 x，y 的值满足 （A） 2y x （B） 3y x （C） 4y x （D） 5y x (10)以抛物线 C 的顶点为圆心的圆交 C 于 A、B 两点，交 C 的标准线于 D、E 两点.已知 |AB|= 4 2 ，|DE|= 2 5 ，则 C 的焦点到准线的距离为 (A)2 (B)4 (C)6 (D)8 (11)平面 a 过正方体 ABCD-A1B1C1D1 的顶点 A，a//平面 CB1D1，a  平面 ABCD=m，a  平面 ABA1B1=n，则 m、n 所成角的正弦值为 (A) 3 2 (B) 2 2 (C) 3 3 (D) 1 3 12. 已 知 函 数 ( ) sin( )( 0 ),2 4f x x+ x        ， 为 ( )f x 的 零 点 ， 4x  为 ( )y f x 图像的对称轴，且 ( )f x 在 5 18 36       ， 单调，则 的最大值为 （A）11 （B）9 （C）7 （D）5 第 II 卷 本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答. 第(22)题~第(24)题为选考题，考生根据要求作答. 二、填空题：本大题共 3 小题，每小题 5 分 (13)设向量 a=(m，1)，b=(1，2)，且|a+b|2=|a|2+|b|2，则 m=. (14) 5(2 )x x 的展开式中，x3 的系数是.（用数字填写答案） （15）设等比数列 满足 a1+a3=10，a2+a4=5，则 a1a2…an 的最大值为。 （16）某高科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料。生产一件产品 A 需要 甲材料 1.5kg，乙材料 1kg，用 5 个工时；生产一件产品 B 需要甲材料 0.5kg，乙材料 0.3kg， 用 3 个工时，生产一件产品 A 的利润为 2100 元，生产一件产品 B 的利润为 900 元。该企业 现有甲材料 150kg，乙材料 90kg，则在不超过 600 个工时的条件下，生产产品 A、产品 B 的 利润之和的最大值为元。 三.解答题：解答应写出文字说明，证明过程或演算步骤. （17）（本题满分为 12 分） ABC 的内角 A，B，C 的对边分别别为 a，b，c，已知 2cos ( cos cos ) .C a B+b A c （I）求 C； （II）若 7,c ABC  的面积为 3 3 2 ，求 ABC 的周长． （18）（本题满分为 12 分） 如图，在已 A，B，C，D，E，F 为顶点的五面体中，面 ABEF 为正方形，AF=2FD， 90AFD   ， 且二面角 D-AF-E 与二面角 C-BE-F 都是 60 ． （I）证明平面 ABEF  EFDC； （II）求二面角 E-BC-A 的余弦值． （19）（本小题满分 12 分） 某公司计划购买 2 台机器，该种机器使用三年后 即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个 200 元.在机器使用期间，如果备件不足再购买，则每个 500 元.现需决策在购买机器时应同时购 买几个易损零件，为此搜集并整理了 100 台这种机器在三年使用期内更换的易损零件数，得 下面柱状图： 以这 100 台机器更换的易损零件数的频率代替 1 台机器更换的易损零件数发生的概率，记 X 表示 2 台机器三年内共需更换的易损零件数，n 表示购买 2 台机器的同时购买的易损零件数. （I）求 X 的分布列； （II）若要求 ( ) 0.5P X n  ，确定 n 的最小值； （III）以购买易损零件所需费用的期望值为决策依据，在 19n  与 20n  之中选其一，应 选用哪个？ 20. （本小题满分 12 分） 设圆 2 2 2 15 0x y x    的圆心为 A，直线 l 过点 B（1,0）且与 x 轴不重合，l 交圆 A 于 C， D 两点，过 B 作 AC 的平行线交 AD 于点 E. （I）证明 EA EB 为定值，并写出点 E 的轨迹方程； （II）设点 E 的轨迹为曲线 C1，直线 l 交 C1 于 M,N 两点，过 B 且与 l 垂直的直线与圆 A 交于 P,Q 两点，求四边形 MPNQ 面积的取值范围. （21）（本小题满分 12 分） 已知函数 有两个零点. (I)求 a 的取值范围； (II)设 x1，x2 是 的两个零点，证明： +x2<2. 请考生在 22、23、24 题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题 号 （22）（本小题满分 10 分）选修 4-1：几何证明选讲 如图，△OAB 是等腰三角形，∠AOB=120°.以⊙O 为圆心， OA 为半径作圆. (I)证明：直线 AB 与 O 相切； (II)点 C,D 在⊙O 上，且 A,B,C,D 四点共圆，证明：AB∥CD. （23）（本小题满分 10 分）选修 4—4：坐标系与参数方程 在直线坐标系 xoy 中，曲线 C1 的参数方程为 （t 为参数，a＞0） 。在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线 C2：ρ=cosθ. （I）说明 C1 是哪种曲线，并将 C1 的方程化为极坐标方程； （II）直线 C3 的极坐标方程为，其中满足 tan=2，若曲线 C1 与 C2 的公共点都在 C3 上，求 a。 （24）（本小题满分 10 分），选修 4—5：不等式选讲 已知函数 f(x)= ∣x+1∣-∣2x-3∣. （I）在答题卡第（24）题图中画出 y= f(x)的图像； （II）求不等式∣f(x)∣﹥1 的解集。 2016 年普通高等学校招生全国统一考试附参考答案和解析 1-12：DBCBA,ADCCB,AB 13：-2 14：10 15：64 16：216000 绝密★启封并使用完毕前 试题类型： 2016 年普通高等学校招生全国统一考试 文科数学 注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、 准考证号填写在答题卡上。 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回. 第Ⅰ卷 三. 选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只 有一项是符合题目要求的。 （1）设集合 {0,2,4,6,8,10}, {4,8}A B  ，则 CAB= （A）{4 8}， （B）{0 2 6}，， （C）{0 2 610}，，， （D）{0 2 4 6 810}，，，，， （2）若 4 3iz   ，则 | | z z = （A）1 （B） 1 （C） 4 3+ i5 5 （D） 4 3 i5 5  （3）已知向量 BA  =（ 1 2 ， 3 2 ）， BC  =（ 3 2 ， 1 2 ），则∠ABC= （A）30°（B）45° （C）60°（D）120° （4）某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平 均最低气温的雷达图。图中 A 点表示十月的平均最高气温约为 15℃，B 点表示四月 的平均最低气温约为 5℃。下面叙述不正确的是 （A）各月的平均最低气温都在 0℃以上 （B）七月的平均温差比一月的平均温差大 （C）三月和十一月的平均最高气温基本相同 （D）平均最高气温高于 20℃的月份有 5 个 （5）小敏打开计算机时，忘记了开机密码的前两位，只记得第一位是 M，I,N 中的一个字 母，第二位是 1,2,3,4,5 中的一个数字，则小敏输入一次密码能够成功开机的概率是 （A） 8 15 （B） 1 8 （C） 1 15 （D） 1 30 （6）若 tanθ= 1 3 ，则 cos2θ= （A） 4 5  （B） 1 5  （C） 1 5 （D） 4 5 （7）已知 4 2 1 3 3 32 , 3 , 25a b c   ，则 (A)b

查看更多