2019届二轮复习第四类　概率问题重在“辨”——辨析、辨型学案（全国通用）

2019届二轮复习第四类　概率问题重在“辨”——辨析、辨型学案（全国通用）

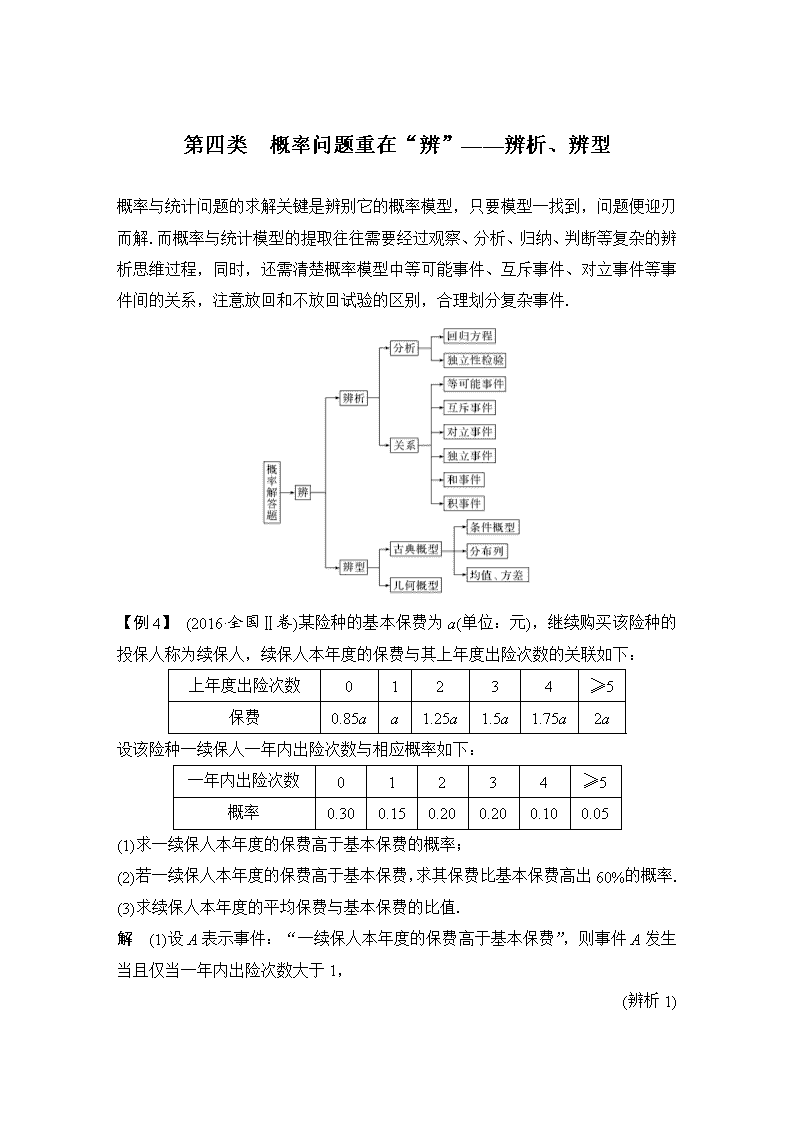
第四类　概率问题重在“辨”——辨析、辨型 概率与统计问题的求解关键是辨别它的概率模型，只要模型一找到，问题便迎刃而解.而概率与统计模型的提取往往需要经过观察、分析、归纳、判断等复杂的辨析思维过程，同时，还需清楚概率模型中等可能事件、互斥事件、对立事件等事件间的关系，注意放回和不放回试验的区别，合理划分复杂事件.‎ ‎【例4】 (2016·全国Ⅱ卷)某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 保费 ‎0.85a a ‎1.25a ‎1.5a ‎1.75a ‎2a 设该险种一续保人一年内出险次数与相应概率如下：‎ 一年内出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎≥5‎ 概率 ‎0.30‎ ‎0.15‎ ‎0.20‎ ‎0.20‎ ‎0.10‎ ‎0.05‎ ‎(1)求一续保人本年度的保费高于基本保费的概率；‎ ‎(2)若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率.‎ ‎(3)求续保人本年度的平均保费与基本保费的比值.‎ 解　(1)设A表示事件：“一续保人本年度的保费高于基本保费”，则事件A发生当且仅当一年内出险次数大于1，‎ ‎(辨析1)‎ 故P(A)＝0.20＋0.20＋0.10＋0.05＝0.55.‎ ‎(辨型1)‎ ‎(2)设B表示事件：“一续保人本年度的保费比基本保费高出60%”，则事件B发生当且仅当一年内出险次数大于3，‎ ‎(辨析2)‎ 故P(B)＝0.10＋0.05＝0.15.‎ 又P(AB)＝P(B)，‎ 故P(B|A)＝＝＝＝.‎ ‎(辨型2)‎ 因此所求概率为.‎ ‎(3)记续保人本年度的保费为X，则X的分布列为 X ‎0.85a a ‎1.25a ‎1.5a ‎1.75a ‎2a P ‎ 0.30‎ ‎0.15‎ ‎0.20‎ ‎0.20‎ ‎0.10‎ ‎0.05‎ ‎(辨型3)‎ E(X)＝0.85a×0.30＋a×0.15＋1.25a×0.20＋1.5a×0.20＋1.75a×0.10＋2a×0.05＝1.23a.‎ 因此续保人本年度的平均保费与基本保费的比值为1.23.‎ 探究提高　1.辨析(1)：判断事件A发生，在一年内出险次数为2，3，4或≥5.‎ 辨型(1)：该问题为求随机事件的概率，利用互斥事件的概率加法公式求解.‎ 辨析(2)：判断事件B发生，在一年内出险次数为4或≥5.‎ 辨型(2)：该问题为条件概率，可利用公式求解.‎ ‎2.求解此类问题的关键：‎ ‎(1)会判断，先判断事件的类型，再利用对立事件的概率公式、条件概率的公式等求解概率；‎ ‎(2)会计算，要求随机变量X的期望，需先求出X的所有可能取值，然后求出随机变量X取每个值时的概率，再利用随机变量的数学期望的定义进行计算.‎ ‎【训练4】 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务，由于其依托“互联网＋”，符合“低碳出行”的理念，已越来越多地引起了人们的关注.‎ 某部门为了对该城市共享单车加强监管，随机选取了50人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这50人根据其满意度评分值(百分制)按照[50，60)，[60，70)，…，[90，100]分成5组，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)的解决下列问题：‎ 频率分布表 组别 分组 频数 频率 第1组 ‎[50，60)‎ ‎8‎ ‎0.16‎ 第2组 ‎[60，70)‎ a ‎■‎ 第3组 ‎[70，80)‎ ‎20‎ ‎0.40‎ 第4组 ‎[80，90)‎ ‎■‎ ‎0.08‎ 第5组 ‎[90，100]‎ ‎2‎ b 合计 ‎■‎ ‎■‎ 频率分布直方图 ‎(1)求出a，b，x的值；‎ ‎(2)若在满意度评分值为[80，100]的人中随机抽取2人进行座谈，设所抽取的2人中来自第5组的人数记为ξ，求ξ的分布列和数学期望.‎ 解　(1)由题意可知，＝，解得b＝0.04；‎ ‎∴样本容量n＝＝50，‎ ‎∴[80，90)内的频数为50×0.08＝4，‎ a＝50－8－20－4－2＝16；‎ 又[60，70)内的频率为＝0.32，∴x＝＝0.032；‎ ‎(2)由题意可知，第4组共有4人，第5组共有2人，‎ ‎∴随机变量ξ的可能取值为0，1，2，‎ P(ξ＝0)＝＝，P(ξ＝1)＝＝，‎ P(ξ＝2)＝＝.‎ ‎∴ξ的分布列为：‎ ξ ‎0‎ ‎1‎ ‎2‎ P ‎∴E(ξ)＝0×＋1×＋2×＝.‎