2018届二轮复习 三角函数的图象与性质 课件 （全国通用）

2018届二轮复习 三角函数的图象与性质 课件 （全国通用）

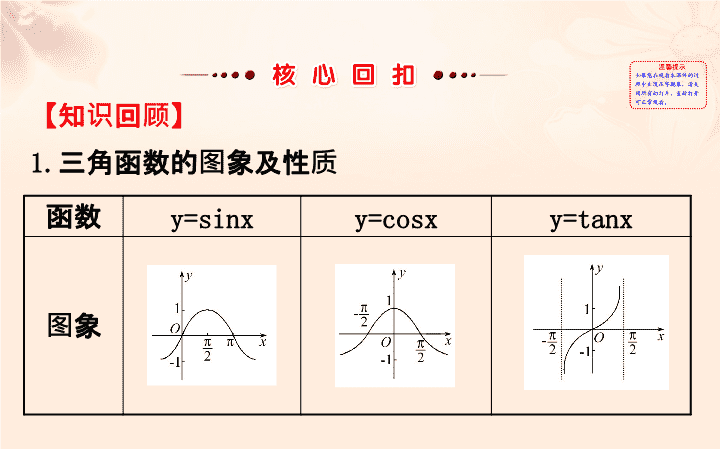
第一讲 　 三角函数的图象与性质 【 知识回顾 】 1. 三角函数的图象及性质 函数 y= sinx y= cosx y= tanx 图象 函数 y= sinx y= cosx y= tanx 单调性 在 _____________ _______ 上递增 , 在 ___________ _______ 上递减 在 __________ ____________ 上递增 , 在 _______ _________ _______ 上递减 在 __________ __________ _______ 上都是 增函数 ( k∈Z ) ( k∈Z ) [2kπ-π, 2kπ](k∈Z) [2kπ, 2kπ+π] ( k∈Z ) ( k∈Z ) 函数 y= sinx y= cosx y= tanx 对称中 心坐标 _____________ __________ __________ 对称轴 方程 ___________ ___________ (kπ,0),k∈Z x= kπ,k∈Z 2. 三角函数图象的两种变换方法 横坐标 | φ | 横坐标 纵坐标 纵坐标 【 易错提醒 】 1. 忽视定义域 : 求解三角函数的单调区间、最值 ( 值域 ) 以及作图象等问题时 , 要注意函数的定义域 . 2. 忽视图象变换顺序 : 在图象变换过程中 , 注意分清是先相位变换 , 还是先周期变换 . 变换只是对于其中的自变量 x 而言的 , 如果 x 的系数不是 1, 就要把这个系数提取后再确定变换的单位长度和方向 . 3. 忽视 A,ω 的符号 : 在求 y= Asin(ωx+ φ ) 的单调区间时 , 要特别注意 A 和 ω 的符号 , 若 ω<0, 需先通过诱导公式将 x 的系数化为正的 . 【 考题回访 】 1.(2016 · 全国卷 Ⅱ) 若将函数 y=2sin2x 的图象向左平 移 个单位长度 , 则平移后图象的对称轴为　 ( 　　 ) 【 解析 】 选 B. 平移后图象的解析式为 y=2sin2 , 令 得对称轴方程 :x= ( k∈Z ). 2.(2014 · 全国卷 Ⅰ) 在函数① y=cos|2x|,②y=| cosx |, ③y= cos ,④y=tan 中 , 最小正周期为 π 的所有函数为　 ( 　　 ) A.①②③ B.①③④ C.②④ D.①③ 【 解析 】 选 A. 由 y= cosx 是偶函数可知 y=cos|2x|=cos2x, 最小正周期为 π , 即①正确 ;y=| cosx | 的最小正周期也 是 π , 即②也正确 ;y= cos 最小正周期为 π , 即③ 正确 ;y=tan 的最小正周期为 , 即④不正确 . 即 正确答案为①②③ . 3.(2016 · 全国卷 Ⅲ) 函数 y= sinx - cosx 的图象可由 函数 y= sinx + cosx 的图象至少向右平移 ________ 个 单位长度得到 . 【 解析 】 函数 y= sinx - cosx =2sin , 根据左加 右减原则可得只需将 y= sinx + cosx 的图象向右平移 个单位即可 . 答案 : 4.(2014 · 全国卷 Ⅱ) 函数 f(x )=sin(x+ φ )-2sin φ cosx 的最大值为 ________. 【 解析 】 f(x )=sin(x+ φ )-2sin φ cosx =sinxcos φ +cosxsin φ -2sin φ cosx = sinxcos φ -cosxsin φ =sin(x- φ )≤1, 故最大值为 1. 答案 : 1 热点考向一 　三角函数的定义域、值域、最值 命题解读 : 主要考查三角函数的定义域、值域、最值的求法 , 以及根据函数的值域和最值求参数的值 . 以选择题、填空题为主 . 【 典例 1】 (1)(2016 · 茂名一模 ) 函数 y= lg(sinx )+ 的定义域为 ________. (2)(2016 · 葫芦岛一模 ) 已知函数 f(x )= cosx · sin - cos 2 x+ , x∈R , 则 f(x ) 在闭区间 上的值域为 ______. 【 解题导引 】 (1) 构建不等式组 , 利用三角函数的图象求解 . (2) 利用三角函数的恒等变换及三角函数的单调性求解 . 【 规范解答 】 (1) 要使函数有意义必须有 即 解得 ( k∈Z ), 所以 2kπ0 时 , 由 - ≤ x ≤ 得 - ω≤ωx ≤ ω, 由题意知 ,- ω≤- , 所以 ω≥ , 当 ω<0 时 , 由 - ≤x≤ 得 ω≤ωx ≤- ω, 由题意知 , ω≤- , 所以 ω≤-2, 综上知 ω∈(-∞,-2]∪ 2.(2016 · 长沙一模 ) 已知函数 f(x )=sin , 其中 x∈ , 若 f(x ) 的值域是 , 则 a 的取值范围是 ________. 【 解析 】 若 - ≤ x ≤ a , 则 - ≤2x≤2a,- ≤2x+ ≤2a+ . 因为当 2x+ =- 或 2x+ = 时 , 所以要使 f(x ) 的值域是 , 则有 ≤ 2a+ ≤ , 即 ≤ 2a≤π, 所以 ≤ a≤ , 即 a 的取值范围是 . 答案 : 3. 当 x∈ 时 , 函数 y=3-sinx-2cos 2 x 的最大值是 ________. 【 解析 】 因为 0) 满足 : 且在区间 内有最大值但没有最小值 . 给出下列 四个命题 : p 1 :f(x) 在区间 [0,2π] 上单调递减 ; p 2 :f(x) 的最小正周期是 4π; p 3 :f(x) 的图象关于直线 x= 对称 ; p 4 :f(x) 的图象关于点 对称 . 其中的真命题是　 ( 　　 ) A.p 1 ,p 2 　 B.p 1 ,p 3 　 C.p 2 ,p 4 　 D.p 3 ,p 4 (3)(2016 · 全国卷 Ⅰ) 已知函数 f(x )= sin(ωx+ φ ) x=- 为 f(x ) 的零点 ,x= 为 y= f(x ) 图象 的对称轴 , 且 f(x ) 在 上单调 , 则 ω 的最大值 为 ( 　　 ) A.11 B.9 C.7 D.5 【 解题导引 】 (1) 由周期求得 ω, 利用特殊点求得 φ , 进而求出函数的单调区间 . (2) 利用 确定函数的对称轴 , 然后根据给出的命题 , 利用三角函数的性质逐一判断 . (3) 根据 x=- 为 f(x ) 的零点 ,x= 为 y= f(x ) 图象的对称轴能得到 w 的取值范围 , 再根据 f(x ) 的单调性结合选项从大到小验证得答案 . 【 规范解答 】 (1) 选 D. 由五点作图知 , 解得 ω= π, φ = , 所以 f(x )= cos(πx + ), 令 2kπ< πx + <2kπ+π,k∈Z, 解得 2k- 0) 的单调区间时 , 令 ωx+ φ =z, 则 y= Asinz ( 或 y= Acosz ), 然后由复合函数的单调性 求得 . ② 图象法 : 画出三角函数的图象 , 结合图象求其单调区间 . (2) 判断对称中心与对称轴 : 利用函数 y= Asin(ωx+ φ ) 的对称轴一定经过图象的最高点或最低点 , 对称中心一定是函数的零点这一性质 , 通过检验 f(x 0 ) 的值进行判断 . (3) 三角函数的周期的求法 :① 定义法 ;② 公式法 :y= Asin(ωx+ φ ) 和 y= Acos(ωx+ φ ) 的最小正周期为 ,y= tan(ωx+ φ ) 的最小正周期为 .③ 利用图象 . 【 题组过关 】 1. 下列函数中 , 最小正周期为 π 且图象关于原点对称的函数是　 ( 　　 ) A.y=cos B.y=sin C.y=sin2x+cos2x D.y=sinx+cosx 【 解析 】 选 A. 采用验证法 . 由 y= cos =-sin2x, 可知该函数的最小正周期为 π 且为奇函数 . 2.(2016 · 洛阳一模 ) 若函数 y= cos ( ω∈N * ) 图象的一个对称中心是 , 则 ω 的最小值为 ( 　　 ) A.1 B.2 C.4 D.8 【 解析 】 选 B. ( k ∈ Z ) 得 ω =6k+2(k ∈ Z), 又 ω∈N * , 所以 ω min =2, 故选 B. 3.(2016 · 日照一模 ) 已知函数 f(x )= sin(ωx+ φ ) 的最小正周期是 π, 若将其图象向右 平移 个单位后得到的图象关于原点对称 , 则函数 f(x ) 的图象　 ( 　　 ) A. 关于直线 x= 对称　　 B. 关于直线 x= 对称 C. 关于点 对称　　 D. 关于点 对称 【 解析 】 选 B. 因为 f(x ) 的最小正周期为 π , 所以 = π,ω =2, 所以 f(x ) 的图象向右平移 个单位后得到 的图象 , 又 g(x ) 的图象关于原点对称 , 所以 - + φ = kπ,k∈Z, φ = + kπ,k∈Z , 又 所以 k=-1, φ =- , 所以 f(x )=sin , 当 x= 时 ,2x- =- , 所以 A,C 错误 , 当 x= 时 ,2x- = , 所以 B 正确 ,D 错误 . 【 加固训练 】 1. 已知函数 f(x )= Acos(ωx+ φ )(A >0,ω>0, φ ∈R), 则 “ f(x ) 是奇函数 ” 是 “ φ = ” 的　 ( 　　 ) A. 充分不必要条件　 B. 必要不充分条件 C. 充分必要条件　 D. 既不充分也不必要条件 【 解析 】 选 B. 若 f(x ) 是奇函数 , 则 f(0)=0, 所以 cos φ =0, 所以 φ = + kπ(k∈Z ), 故 φ = 不成立 ; 若 φ = , 则 f(x )= Acos =- Asinωx,f(x ) 是奇函数 . 所以 f(x ) 是奇函数是 φ = 的必要不充分条件 . 2.(2016 · 大庆一模 ) 已知函数① y= sinx+cosx , ②y=2 sinxcosx , 则下列结论正确的是　 ( 　　 ) A. 两个函数的图象均关于点 成中心对称图形 B. 两个函数的图象均关于直线 x=- 成轴对称图形 C. 两个函数在区间 上都是单调递增函数 D. 两个函数的最小正周期相同 【 解析 】 选 C. 令 f(x )= sinx+cosx = sin , g(x )=2 sinxcosx = sin2x. 对于 A,B,f =0, g =- ≠ 0, 所以 A,B 都不正确 . 对于 C, 由 - +2kπ≤x+ ≤ +2kπ(k∈Z), 得 f(x ) 的单调递增区间为 ( k∈Z ), 又由 - +2kπ≤2x≤ +2kπ(k∈Z), 得 g(x ) 的单调递 增区间为 ( k∈Z ), 易知 C 正确 . 对于 D,f(x ) 的最小正周期为 2π,g(x) 的最小正周期为 π,D 不正确 . 3.(2016 · 石家庄二模 ) 已知函数 f(x )= sinωx+cosωx (ω>0),x∈R. 若函数 f(x ) 在区间 (- ω,ω ) 内单调递增 , 且函数 y= f(x ) 的图象关于直线 x=ω 对称 , 则 ω 的值为 __________. 【 解析 】 f(x )= sin ω x+cos ω x = sin , 因为 f(x ) 在区间 (- ω,ω ) 内单调递增 , 且函数图象关于直线 x=ω 对称 , 所以 f(ω ) 必为一个周期上的最大值 , 所以有 ω · ω + =2kπ+ , k∈Z , 所以 ω 2 = +2kπ,k∈Z. 又 ω-(-ω )≤ , 即 ω 2 ≤ , 所以 ω 2 = , 所以 ω= . 答案 : 热点考向三 　三角函数的图象及应用 命题解读 : 主要考查三角函数的图象变换 , 或根据图象求解析式或参数 , 三种题型都有可能出现 , 如果是解答题 , 一般考查综合应用 . 命题角度一　三角函数的图象及其变换 【 典例 3】 (1)(2016 · 临沂一模 ) 函数 f(x )= sin(ωx+ φ ) 的图象如图所示 , 为了得到 g(x )= sinωx 的图象 , 只需把 y= f(x ) 的图象上所有点 ( 　　 ) A. 向右平移 个单位长度 B. 向右平移 个单位长度 C. 向左平移 个单位长度 D. 向左平移 个单位长度 (2)(2016 · 安康二模 ) 已知函数 f(x )= Asin(ωx + φ )(A,ω, φ 是常数 ,A>0,ω>0,0≤ φ ≤π) 的部分图象如图所示 , 其中 M,N 两点之间的距离为 5, 则 f(6)=__________. 【 解题导引 】 (1) 先求出 f(x),g(x ) 的解析式 , 再判断平移情况 . (2) 设 M(x 1 ,2),N(x 2 ,-2), 利用两点间的距离求出 | x 1 -x 2 | , 确定函数的周期 , 利用周期性求解 . 【 规范解答 】 (1) 选 A. 由图象知 : 所以 T=π. 又 π= , 所以 ω=2. 由 f =0 得 :2× + φ = kπ(k∈Z ), 即 φ = kπ - ( k∈Z ). 因为 | φ |< , 所以 φ = , 即 f(x )= (2) 由题图可知 A=2, 因为 M,N 两点分别为函数图象上相邻的最高点和最低点 , 设 M(x 1 ,2),N(x 2 ,-2), 因为 |MN|=5, 所以 =5, 解得 |x 1 -x 2 |=3, 因为 M,N 两点横坐标之差的绝对值为最小正周期的一半 , 即 =3, 解得 T=6, 所以 f(6)=f(0)=1. 答案 : 1 【 母题变式 】 1. 若典例 (2) 中条件不变 , 求 f(2 017) 的值 . 【 解析 】 由例题解析可知 ,T=6, 所以 =6, 解得 ω= , 又因为 f(0)=1, 所以 2sin φ =1, 解得 sin φ = , 因为 0≤ φ ≤π, 所以 φ = 或 φ = , 结合图象 φ = 不符合题意 , 舍去 , 故 φ = , 所以 f(x)=2sin . 又 f(2 017)=f(336×6+1)=f(1), 而 f(1)=2sin =-1. 2. 若将典例 (2) 中图象变为如图所示的图象 , 求 f(x ) 的解析式 . 【 解析 】 由题图知 A= , 以 M 为第一个零点 , N 为第二个零点 . 列方程组 解得 所以所求解析式为 y= sin 命题角度二　三角函数的图象与性质的综合应用 【 典例 4】 (2016 · 湖州一模 ) 已知函数 f(x )= 2sinωxcosωx+2 sin 2 ωx- (ω>0) 的最小正 周期为 π. (1) 求函数 f(x ) 的单调增区间 . (2) 将函数 f(x ) 的图象向左平移 个单位 , 再向上平移 1 个单位 , 得到函数 y= g(x ) 的图象 , 若 y= g(x ) 在 [0,b](b>0) 上至少含有 10 个零点 , 求 b 的最小值 . 【 题目拆解 】 解答本题第 (2) 问 , 可拆解成三个小题 : ① 求 g(x ) 的解析式 ; ② 求方程 g(x )=0 的解 ; ③ 求 b 的最小值 . 【 规范解答 】 (1) 由题意得 f(x )=2sinωxcosωx+ 2 sin 2 ωx- =sin2ωx- cos2ωx=2sin , 由最小正周期为 π, 得 ω=1, 所以 f(x )=2sin , 由 2kπ- ≤2x- ≤2kπ+ , k∈Z , 整理得 kπ - ≤ x≤kπ + , k∈Z , 所以函数 f(x ) 的单调增区间是 , k∈Z . (2) 将函数 f(x ) 的图象向左平移 个单位 , 再向上平移 1 个单位 , 得到 y=2sin2x+1 的图象 , 所以 g(x )=2sin2x+1. 令 g(x )=0, 得 x= kπ + 或 x= kπ + ( k∈Z ), 所以在 [0,π] 上恰好有两个零点 , 若 y= g(x ) 在 [0,b] 上 有 10 个零点 , 则 b 不小于第 10 个零点的横坐标即可 , 即 b 的最小值为 【 规律方法 】 1. 函数表达式 y= Asin(ωx+ φ )+B 的确定方法 字母 确定途径 说　　明 A 由最值确定 A= B 由最值确定 B= 字母 确定途径 说　　明 ω 由函数的 周期确定 相邻的最高点与最低点的横坐标 之差的绝对值为半个周期 , 最高点 ( 或最低点 ) 的横坐标与相邻零点 差的绝对值为 个周期 φ 由图象上的 特殊点确定 一般把第一个零点作为突破口 , 可以从图象的升降找准第一个 零点的位置 . 利用待定系数法并 结合图象列方程或方程组求解 2. 三角函数图象平移问题处理策略 (1) 看平移要求 : 首先要看题目要求由哪个函数平移得到哪个函数 , 这是判断移动方向的关键点 . (2) 看移动方向 : 移动的方向一般记为 “ 正向左 , 负向右 ” , 看 y= Asin(ωx+ φ ) 中 φ 的正负和它的平移要求 . (3) 看移动单位 : 在函数 y= Asin(ωx+ φ ) 中 , 周期变换和 相位变换都是沿 x 轴方向的 , 所以 ω 和 φ 之间有一定的关 系 , φ 是初相 , 再经过 ω 的压缩 , 最后移动的单位是 . 【 题组过关 】 1.(2016 · 保定一模 ) 为得到函数 y=sin 的图象 , 可将函数 y= sinx 的图象向左平移 m 个单位长度 , 或向 右平移 n 个单位长度 ( m,n 均为正数 ), 则 | m-n | 的最小值 是　 ( 　　 ) 【 解析 】 选 B. 由题意可知 ,m= +2k 1 π ,k 1 为非负整数 , n=- +2k 2 π,k 2 为正整数 , 所以 | m-n |= , 所以当 k 1 =k 2 时 ,| m-n| min = . 2.(2016 · 九江一模 ) 将函数 f(x )=sin(2x+ φ )(| φ |<π) 的图象向左平移 个单位后得到函数 g(x )= cos 的图象 , 则 φ 的值为　 ( 　　 ) 【 解析 】 选 C. 由题意得 g(x )= 又 g(x )= cos =sin , 所以 + φ =2kπ+ , k∈Z , 即 φ =2kπ+ , k∈Z , 因为 | φ |<π, 所以 φ = . 3.(2016 · 南昌二模 ) 函数 f(x )= Asin(ωx+ φ ) 的部分图象如图所示 , 若 x 1 ,x 2 ∈ , 且 f(x 1 )=f(x 2 ), 则 f(x 1 +x 2 )= 　 ( 　　 ) 【 解析 】 选 D. 观察图象可知 ,A=1,T= π , 所以 ω=2,f(x)=sin(2x+ φ ). 将 代入上式得 sin =0, 由 | φ |< , 得 φ = , 则 f(x )=sin . 函数图象的对称轴为 x= 又 x 1 ,x 2 ∈ 且 f(x 1 )=f(x 2 ), 所以 所以 x 1 +x 2 = , 所以 f(x 1 +x 2 )= 【 加固训练 】 1.(2016 · 武汉一模 ) 已知函数 f(x )=sin(2x+ )( x∈R ), 把函数 f(x ) 的图象向右平移 个单位长度得函数 g(x ) 的图象 , 则下列结论错误的是　 ( 　　 ) A. 函数 g(x ) 在区间 上为增函数 B. 函数 g(x ) 为偶函数 C. 函数 g(x ) 的最小正周期为 π D. 函数 g(x ) 的图象关于直线 x= 对称 【 解析 】 选 D. 因为 f(x )=sin ( x ∈ R ), 所以 g(x )=sin =-cos2x, 故函数 g(x ) 的最小正 周期 T= =π, 函数 g(x ) 为偶函数 , 且 , 故函数 g(x ) 的图象不关于直线 x= 对称 , 当 0≤x≤ 时 ,0≤2x≤π, 则函数 g(x ) 在区间 上为增函数 , 故选 D. 2.(2016 · 秦皇岛一模 ) 已知函数 f(x )= cos(ωx+ φ - ) 的部分图象如图所示 , 则 取得最 小值时 x 的取值集合为　 ( 　　 ) 【 解析 】 选 B. 因为 f(x )= cos = sin( ω x+ φ ), 由题图可知 又由题图得 sin 即 2× + φ =2kπ+ , k∈Z , 所以 φ =2kπ- , k∈Z , 又 | φ |< , 所以 φ =- , 所以 f(x )=sin , 则 由 2x+ =- +2kπ,k∈Z, 得 x= kπ - , k∈Z , 所以 y=f 取得最小值时 x 的取值集合为 3.(2016 · 安庆二模 ) 已知函数 f(x )= Asin(ωx+ φ ) (A>0,ω>0,| φ |< ) 的部分图象如图所示 , 则 f(x ) 的递增区间为 ( 　　 ) 【 解析 】 选 B. 由图象可知 A= 所以 T=π, 故 ω=2. 由五点法作图可得 2 · + φ =0, 求得 φ =- , 所以 , f(x )=2sin , 由 2x- ∈ ( k∈Z ), 得 x∈ ( k∈Z ), 所以 f(x ) 的单调递增区间是 ( k∈Z ).