【物理】2020届一轮复习人教版专题五求解变力做功的方法学案
专题五:求解变力做功的方法
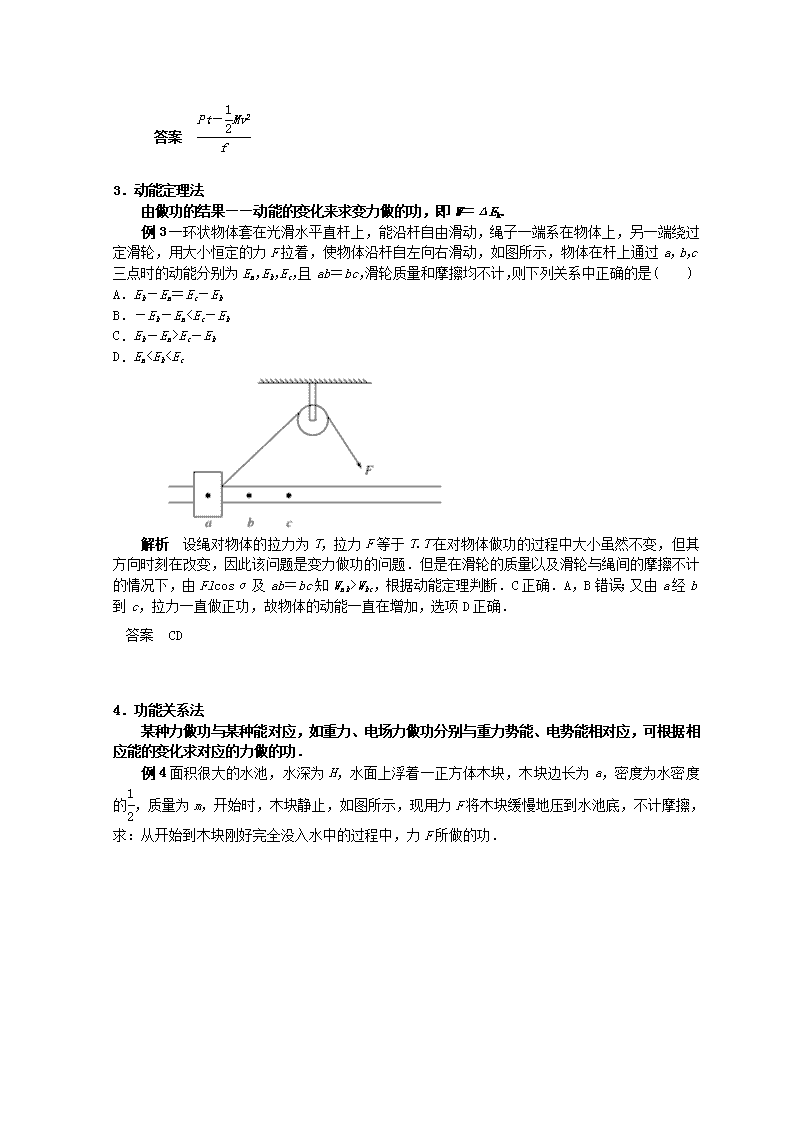
1.等值法
若某一变力做的功和某一恒力做的功相等,则可以通过计算该恒力做的功,求出该变力做的功.恒力做功又可以用W=Fscosα计算.
例1如图,定滑轮至滑块的高度为h,已知细绳的拉力为F(恒定),滑块沿水平面由A点前进s至B点,滑块在初、末位置时细绳与水平方向夹角分别为α和β.求滑块由A点运动到B点的过程中,绳的拉力对滑块所做的功.(不考虑绳、滑轮的摩擦和滑轮的质量).
解析 设绳对滑块的拉力为T,显然T与F大小相等,细绳的拉力在对滑块做功的过程中大小虽然不变,但其方向时刻在改变,因此该问题是变力做功的问题.拉力F的大小和方向都不变,可以用公式W=Fscosα直接计算.由图可知,在绳与水平面的夹角由α变到β的过程中,拉力F的位移大小为
Δs=s1-s2=-
故WF=F·Δs=Fh.
答案 Fh
2.功率法
若功率恒定,可根据W=Pt求变力做的功.
例2一列火车由机车牵引沿水平轨道行驶,经过时间t,其速度由0增大到v.已知列车总质量为M,机车功率P保持不变,列车所受阻力f为恒力.求这段时间内列车通过的路程.
解析
错解:以列车为研究对象,水平方向受牵引力F和阻力f.
根据P=Fv可知牵引力F=P/v,
设列车通过的路程为s,根据动能定理有(F-f)s=Mv2,
联立解得s=.
正解:以列车为研究对象,列车水平方向受牵引力和阻力.设列车通过的路程为s,根据动能定理有WF-Wf=Mv2-0.因为列车功率一定,由P=,可知牵引力做的功WF=Pt,联立解得s=.
答案
3.动能定理法
由做功的结果——动能的变化来求变力做的功,即W=ΔEk.
例3一环状物体套在光滑水平直杆上,能沿杆自由滑动,绳子一端系在物体上,另一端绕过定滑轮,用大小恒定的力F拉着,使物体沿杆自左向右滑动,如图所示,物体在杆上通过a,b,c三点时的动能分别为Ea,Eb,Ec,且ab=bc,滑轮质量和摩擦均不计,则下列关系中正确的是( )
A.Eb-Ea=Ec-Eb
B.-Eb-Ea
Ec-Eb
D.EaWbc,根据动能定理判断.C正确.A,B错误;又由a经b到c,拉力一直做正功,故物体的动能一直在增加,选项D正确.
答案 CD
4.功能关系法
某种力做功与某种能对应,如重力、电场力做功分别与重力势能、电势能相对应,可根据相应能的变化求对应的力做的功.
例4面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水密度的,质量为m,开始时,木块静止,如图所示,现用力F将木块缓慢地压到水池底,不计摩擦,求:从开始到木块刚好完全没入水中的过程中,力F所做的功.
解析 解法一:因水池面积很大,可忽略因木块压入而引起的水深的变化,木块刚好完全没入水中时,图中原来画线区域的水被推开,相当于这部分水平铺于水面,这部分水的质量为m,其势能的改变量为:
ΔE水=mgH-mg=mga
木块势能的改变量为:
ΔEm=mg-mgH=-mga
根据动能定理,力F做的功为:
W=ΔE水+ΔEm=mga.
解法二:从开始到木块完全没入水中的过程,力F所做的功为变力功.也可画出F-s图象,做功在数值上等于F-s图线与位移s轴所围图形的面积的数值,在压下木块过程中,力F与位移s成正比,从开始到完全没入水中,力F的位移为a, 作出F-s图象如图,据图象可求得做功W=×amg=mga.
答案 mga
5.平均力法
如果力的方向不变,力的大小随位移按线性规律变化时,可用力的算术平均值(恒力)代替变力,利用功的定义式W=Fscosθ来求功.
6.图象法
如果参与做功的力是变力,方向与位移方向始终一致而大小随时间变化,我们可作出该力随位移变化的图象.如图所示,那么曲线与坐标轴所围的面积,即为变力做的功.
例5用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1 cm.问击第二次时,能击入多少深度?(设铁锤每次做功相等)
解析
解法一:平均力法
铁锤每次做的功都用来克服铁钉阻力,但摩擦阻力不是恒力,其大小与铁钉的击入深度成正比,即f=kx,而摩擦阻力可用平均阻力来代替.
如图甲所示,第一次击入深度为x1,平均阻力=kx1,做功为W1=1x1=kx.
第二次击入深度为x1到x2,平均阻力2=k(x2+x1),
位移为x2-x1,
做功为W2=2(x2-x1)=k(x-x).
两次做功相等W1=W2,解得x2=x1=1.41 cm,故Δx=x2-x1=0.41 cm.
解法二:图象法
因为阻力F=kx,以F为纵坐标,F方向上的位移x为横坐标,作出F-x图象,如图乙所示.曲线与横坐标轴所围面积的值等于阻力F对铁钉做的功.
由于两次做功相等,故有:
S1=S2(面积),
即kx=k(x2+x1)(x2-x1),
故Δx=x2-x1=0.41 cm.
答案 0.41 cm
7.极限法(极端法)
极限法是把某个物理量推向极端,即极大和极小或极左和极右,并依此作出科学的推理分析,从而给出判断或导出一般结论的思维方法.
极限法在进行某些物理过程的分析时,具有独特的作用,恰当地应用极限法能提高解题效率,使问题化难为易,化繁为简.
例6如图所示,用竖直向下的恒力F通过跨过光滑定滑轮的细线拉动静止在光滑水平面上的物体,物体沿水平面移动过程中经过A、B、C三点,设AB=BC,物体经过A、B、C三点时的动能分别为EkA,EkB,EkC,则它们之间满足的关系是( )
A.EkB-EkA=EkC-EkB B.EkB-EkAEkC-EkB D.EkC<2EkB
解析 此题中物体受到的拉力大小恒定,但与水平方向的夹角逐渐增大,属于变力做功问题,求拉力做的功可转化为恒力做功问题.设物体在A、B、C三点时到滑轮的距离分别为L1、L2、L3,则W1=F(L1-L2),W2=F(L2-L3),要比较W1和W2的大小,只需要比较(L1-L2)和(L2-L3)的大小.由于从L1到L3的过程中,绳与水平方向的夹角逐渐变大,所以可以把夹角推到两个极端情况.L1与水平方向的夹角很小,推到接近于0°时,则L1-L2≈AB;L3与水平方向的夹角较大,推到接近90°时,则L2-L3≈0,由此可知,L1-L2>L2-L3,故W1>W2,再由动能定理可判断C、D正确.
答案 CD
8.微元法
在使用微元法处理问题时,需将其分解为众多微小的“元过程”,而且每个“元过程”所遵循的规律是相同的,这样,我们只需分析这些“元过程”,然后再对“元过程”运用必要的数学方法或物理思想处理,进而使问题得到解决.
当物体在变力的作用下做曲线运动时,若力的方向与物体运动的切线方向之间的夹角不变,且力的方向与位移的方向同步变化,则可用微元法将曲线分成无限个小元段,每一小元段可认为是恒力做功,那么总功即为各个小元段做功的代数和.
例7如图所示,将质量为m的物体从山脚拉到高为h的山顶,且拉力总是与物体所经过的坡面平行,已知物体与坡面的动摩擦因数为μ,山脚到山顶的水平距离为s,求将物体从山脚拉到山顶克服摩擦力做多少功?
解析 物体在拉力作用下从山脚拉到山顶,由于摩擦力在山坡的不同位置方向、大小都发生变化,要求出克服摩擦力所做的功,可通过取一微元段进行分析,最后求得摩擦力做的总功.如图,设想物体在山坡上通过一微元段ΔL时,摩擦力的大小为f,当ΔL很小时,可认为摩擦力为恒力.
所以物体克服摩擦力做功:
ΔW=fΔL=μmgcosθΔL=μmgΔs,
故克服摩擦力做的总功:
W=∑ΔW=μmgs.
答案 μmgs
9.补偿法
有些问题从表面上看无从下手,或者由题设条件很难直接求解.但是,在与原题条件不相违背的前提下,如果适当地补偿一定的物理模型、物理装置,或者一定的物理过程、物理量等,补缺求整,往往可使问题由“繁”变“简”,从而解决问题.这种思维方法称为补偿法.
例8 如图所示,质量为M的机车,牵引质量为m的车厢在水平轨道上匀速前进,某时刻车厢与机车脱钩,机车在行驶L路程后,司机发现车厢脱钩,便立即关闭发动机让机车自然滑行,该机车与车厢运动中所受阻力都是其车重的k倍,且恒定不变.试求当机车和车厢都停止运动时,机车和车厢的距离.
解析 所求机车与车厢的距离等于车厢与机车脱钩后二者位移之差,题中只涉及位移、力、速度,故可利用牛顿运动定律、动能定理等多种知识求解.
解法一:运用动能定理求解
所设各量如题图所示,对机车脱钩后的全过程应用动能定理
对机车:F·L-kMg·s1=0-Mv2
对车厢:-kmg·s2=0-mv2
列车原来做匀速运动,故有F=k(M+m)g
联立可得s1-s2=L.
解法二:补偿法
某时刻车厢与机车脱钩,若司机同时发现车厢脱钩,立即关闭发动机让机车自然滑行,那么该机车与车厢最终会停于同一点.司机晚发现,则牵引力对机车多做的功应等于机车多克服摩擦力做的功,即k(M+m)gL=kMg·s,
解出s=(M+m)L/M.
答案 (M+m)L/M