20122013中考数学试卷分类汇编二次函数

20122013中考数学试卷分类汇编二次函数

中考数学试卷分类汇编 ‎　二次函数 一、选择题 ‎1. （2013山东滨州，7，3分）抛物线可以由抛物线平移得到,则下列平移过程正确的是( )‎ A.先向左平移2个单位,再向上平移3个单位 ‎ B.先向左平移2个单位,再向下平移3个单位 C.先向右平移2个单位,再向下平移3个单位 ‎ D.先向右平移2个单位,再向上平移3个单位 ‎【答案】B ‎【答案】D ‎2. （2013广东广州市，5，3分）下列函数中,当x>0时y值随x值增大而减小的是（ ）．‎ A．y = x2 B．y = x－‎１ ‎ C． y = x D．y = ‎【答案】D ‎3. （2013湖北鄂州，15，3分）已知函数，则使y=k成立的x值恰好有三个，则k的值为（ ）‎ A．0 B．‎1 ‎ C．2 D．3‎ ‎4. （2013山东德州6,3分）已知函数（其中）的图象 如下面右图所示，则函数的图象可能正确的是 第6题图 y x ‎1‎ ‎1‎ O ‎（A）‎ y x ‎1‎ ‎-1‎ O ‎（B）‎ y x ‎-1‎ ‎-1‎ O ‎（C）‎ ‎1‎ ‎-1‎ x y O ‎（D）‎ ‎【答案】D ‎5. （2013山东菏泽，8，3分）如图为抛物线的图像，A、B、C 为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是 ‎ A．a＋b=－1 　B． a－b=－‎1 C． b<‎2a　　　　　 D． ac<0 ‎ ‎【答案】B ‎6. （2013山东泰安，20 ，3分）若二次函数y=ax2+bx+c的x与y的部分对应值如下表：‎ X ‎-7‎ ‎-6‎ ‎-5‎ ‎-4‎ ‎-3‎ ‎-2‎ y ‎-27‎ ‎-13‎ ‎-3‎ ‎3‎ ‎5‎ ‎3‎ 则当x=1时，y的值为 A.5 B.‎-3 C.-13 D.-27‎ ‎【答案】D ‎ ‎7. （2013山东威海，7，3分）二次函数的图象如图所示．当y＜0时，自变量x的取值范围是（ ）．‎ A．－1＜x＜3 B．x＜－‎1 ‎ C． x＞3 D．x＜－1或x＞3‎ ‎【答案】A ‎8. 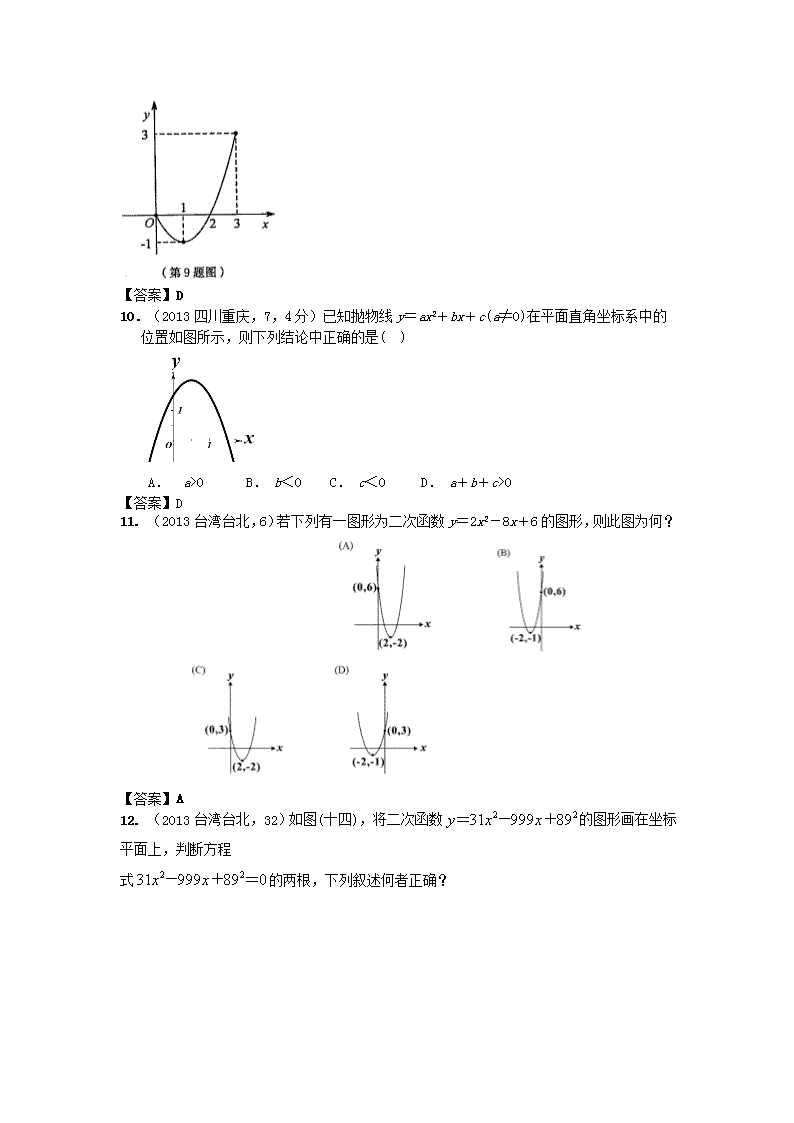（2013山东烟台，10,4分）如图，平面直角坐标系中，两条抛物线有相同的对称轴，则下列关系正确的是（ ）‎ A．m＝n，k＞h B．m＝n ，k＜h ‎ C．m＞n，k＝h D．m＜n，k＝h ‎【答案】A ‎9. （2013浙江温州，9，4分）已知二次函数的图象(0≤x≤3)如图所示．关于该函数在所给自变量取值范围内，下列说法正确的是( )‎ ‎ A．有最小值0，有最大值3 B．有最小值－1，有最大值0‎ ‎ C．有最小值－1，有最大值3 D．有最小值－1，无最大值 ‎【答案】D ‎10．（2013四川重庆，7，4分）已知抛物线y＝ax2＋bx＋c(a≠0)在平面直角坐标系中的位置如图所示，则下列结论中正确的是( )‎ A． a>0 B． b＜‎0 C． c＜0 D． a＋b＋c>0‎ ‎【答案】D ‎11. （2013台湾台北，6）若下列有一图形为二次函数y＝2x2－8x＋6的图形，则此图为何？‎ ‎ ‎ ‎【答案】A ‎12. （2013台湾台北，32）如图(十四)，将二次函数的图形画在坐标平面上，判断方程 式的两根，下列叙述何者正确？‎ A．两根相异，且均为正根 B．两根相异，且只有一个正根 ‎ C．两根相同，且为正根 D．两根相同，且为负根 ‎【答案】A ‎13. （2013台湾全区，28）图(十二)为坐标平面上二次函数的图形，且此图形通（－1 , ‎ ‎1）、（2 ,－1）两点．下列关于此二次函数的叙述，何者正确？‎ A ．y的最大值小于0 B．当x＝0时，y的值大于1‎ C．当x＝1时，y的值大于1 D．当x＝3时，y的值小于0‎ ‎【答案】Ｄ ‎14. （2013甘肃兰州，5，4分）抛物线的顶点坐标是 A．（1，0） B．（－1，0） C．（－2，1） D．（2，－1）‎ ‎【答案】A ‎15. （2013甘肃兰州，9，4分）如图所示的二次函数的图象中，刘星同学观察得出了下面四条信息：（1）；（2）c>1；（3）‎2a－b<0；（4）a+b+c<0。你认为其中错误的有 A．2个 B．3个 C．4个 D．1个 x y ‎-1‎ ‎1‎ O ‎1‎ ‎【答案】D ‎16. （2013江苏宿迁,8,3分）已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图，则下列结论中正确的是（▲）‎ A．a＞0　 　B．当x＞1时，y随x的增大而增大 C．c＜0 D．3是方程ax2＋bx＋c＝0的一个根 ‎【答案】D ‎17. （2013山东济宁，8，3分）已知二次函数中，其函数与自变量之间的部分对应值如下表所示：‎ x ‎……‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎……‎ y ‎……‎ ‎4‎ ‎1‎ ‎0‎ ‎1‎ ‎4‎ ‎……‎ 点A（，）、B（，）在函数的图象上，则当时，与的大小关系正确的是 A． B． C． D． ‎ ‎【答案】B ‎18. （2013山东聊城，9，3分）下列四个函数图象中，当x<0时，函数值y随自变量x的增大而减小的是（ ）‎ ‎【答案】D ‎19. （2013山东潍坊，12，3分）已知一元二次方程的两个实数根、满足和，那么二次函数的图象有可能是（ ）‎ ‎【答案】C ‎20．（2013四川广安，10，3分）若二次函数．当≤l时，随的增大而减小，则的取值范围是（ ） ‎ ‎ A．=l B．>l C．≥l D．≤l ‎【答案】C ‎ ‎21. （2013上海，4，4分）抛物线y＝－(x＋2)2－3的顶点坐标是（ ）．‎ ‎(A) （2，－3）； (B) （－2，3）； (C) （2，3）； (D) （－2，－3） ．‎ ‎【答案】D ‎22. （2013四川乐山5，3分）将抛物线向左平移2个单位后，得到的抛物线的解析式是 ‎ A． B． C． D．‎ ‎【答案】A ‎23. （2013四川凉山州，12，4分）二次函数的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是（ ）‎ 第12题 O x y O y x A O y x B O y x D O y x C ‎【答案】B ‎24. （2013安徽芜湖，10,4分）二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是（ ）.‎ ‎【答案】D ‎25. （2013江苏无锡，9，3分）下列二次函数中，图象以直线x = 2为对称轴，且经过点(0，1)的是 ( )‎ A．y = (x − 2)2 + 1 B．y = (x + 2)2 + 1 ‎ C．y = (x − 2)2 − 3 D．y = (x + 2)2 − 3‎ ‎【答案】C ‎26. （2013江苏无锡，10，3分）如图，抛物线y = x2 + 1与双曲线y = 的交点A的横坐标是1，则关于x的不等式 + x2 + 1 < 0的解集是 ( )‎ A．x > 1 B．x < −‎1 C．0 < x < 1 D．−1 < x < 0‎ ‎（第10题）‎ x y A ‎【答案】D ‎27. （2013湖北黄冈，15，3分）已知函数，则使y=k成立的x值恰好有三个，则k的值为（ ）‎ A．0 B．‎1 ‎ C．2 D．3‎ ‎【答案】D ‎28. （2013广东肇庆，10，3分）二次函数有 A． 最大值 B． 最小值 C． 最大值 D． 最小值 ‎【答案】D ‎29. （2013湖北襄阳，12，3分）已知函数的图象与x轴有交点，则k的取值范围是 A. B. C.且 D.且 ‎【答案】B ‎30. （2013湖南永州，13，3分）由二次函数，可知（ ）‎ A．其图象的开口向下 B．其图象的对称轴为直线 C．其最小值为1 D．当时，y随x的增大而增大 ‎【答案】C．‎ ‎31. (20011江苏镇江,8,2分)已知二次函数,当自变量x取m时,对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值、,则必值,满足 ( )‎ A. >0,>0 B. <0,<‎0 C.<0,>0 D.>0,<0‎ 答案【B 】‎ ‎32. （2013安徽芜湖，10，4分）二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是（ ）.‎ ‎【答案】D ‎33. （2010湖北孝感，12，3分）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为，下列结论：①ac＜0；②a+b=0；③‎4ac－b2=‎4a；④a+b+c＜0.其中正确的个数是（ ）‎ A. 1 B. ‎2 C. 3 D. 4‎ ‎【答案】C ‎34. （2013湖南湘潭市，8，3分）在同一坐标系中，一次函数与二次函数的图像可能是 ‎【答案】C ‎35.‎ 二、填空题 ‎1. （2013浙江省舟山，15，4分）如图，已知二次函数的图象经过点（－1，0），（1，－2），当随的增大而增大时，的取值范围是　 　． ‎ ‎（第15题）‎ ‎（1,-2）‎ ‎-1‎ ‎【答案】‎ ‎2. （2013山东日照，17，4分）如图，是二次函数 y＝ax2＋bx＋c（a≠0）的图象的一部分， 给出下列命题 ：①a+b+c=0；②b＞‎2a；③ax2+bx+c=0的两根分别为-3和1；④a-2b+c＞0．其中正确的命题是 ．（只要求填写正确命题的序号）‎ ‎【答案】①③．‎ ‎3. （2013 浙江杭州，23， 10)设函数 (k为实数)．‎ ‎(1)写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图象；‎ ‎(2)根据所画图象，猜想出：对任意实数K，函数的图象都具有的特征，并给予证明；‎ ‎(3)对任意负实数k，当x0时，y随x的增大而减小.这个函数解析式为_________________________（写出一个即可）‎ ‎【答案】如：等，写出一个即可. ‎ ‎10．（ 2013重庆江津， 18，4分）将抛物线y=x2－2x向上平移3个单位,再向右平移4个单位等到的抛物线是_______.‎ ‎【答案】y=(x-5)2+2 或 y=x2-10x+27‎ ‎11. （2013江苏淮安，14，3分）抛物线y=x2-2x-3的顶点坐标是 . ‎ ‎【答案】（1，-4）‎ ‎12. （2013贵州贵阳，14，4分）写出一个开口向下的二次函数的表达式______．‎ ‎ 【答案】y=-x2+2x+1‎ ‎13. （2013广东茂名，15，3分）给出下列命题：‎ 命题1．点(1，1)是双曲线与抛物线的一个交点．‎ 命题2．点(1，2)是双曲线与抛物线的一个交 点．‎ 命题3．点(1，3)是双曲线与抛物线的一个交点．‎ ‎……‎ 请你观察上面的命题,猜想出命题(是正整数): ‎ ‎【答案】点(1，n)是双曲线与抛物线的一个交点 ．‎ ‎14. （2013山东枣庄，18，4分）抛物线上部分点的横坐标，纵坐标的对应值如下表：‎ x ‎…‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎0‎ ‎4‎ ‎6‎ ‎6‎ ‎4‎ ‎…‎ 从上表可知，下列说法中正确的是 　　 ．（填写序号）‎ ‎①抛物线与轴的一个交点为（3,0）； ②函数的最大值为6；‎ ‎③抛物线的对称轴是；　 　　④在对称轴左侧，随增大而增大．‎ ‎【答案】①③④‎ ‎15. ‎ 三、解答题 ‎1. （2013广东东莞，15，6分）已知抛物线与x轴有交点．‎ ‎ (1)求c的取值范围；‎ ‎(2)试确定直线y＝cx+l经过的象限，并说明理由．‎ ‎【答案】（1）∵抛物线与x轴没有交点 ‎∴⊿＜0，即1－2c＜0‎ 解得c＞‎ ‎(2)∵c＞‎ ‎∴直线y=x＋1随x的增大而增大，‎ ‎∵b=1‎ ‎∴直线y=x＋1经过第一、二、三象限 ‎2. （ 2013重庆江津， 25，10分）已知双曲线与抛物线y=zx2+bx+c交于A(2,3)、B(m,2)、c(－3,n)三点.‎ ‎ (1)求双曲线与抛物线的解析式;‎ ‎ (2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积,‎ ‎·A(2,3)‎ y x ‎1‎ ‎1‎ o 第25题图 ‎-1‎ ‎-1‎ ‎·B(2,3)‎ ‎·C(-2,-3)‎ y x ‎1‎ ‎1‎ o 第25题图 ‎-1‎ ‎-1‎ ‎ 【答案】(1)把点A(2,3)代入得 ：k=6·‎ ‎ ∴反比例函数的解析式为：·‎ ‎ 把点B(m,2)、C(－3,n)分别代入得： m=3,n=-2·‎ ‎ 把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax2+bx+c得：‎ ‎ 解之得 ‎ ‎∴抛物线的解析式为：y=-·‎ ‎(2)描点画图 S△ABC=(1+6)×5-×1×1-×6×4==5·‎ ‎3. （2013江苏泰州，27，12分）已知：二次函数y=x2＋bx－3的图像经过点P（－2,5）．‎ ‎（1）求b的值，并写出当1＜x≤3时y的取值范围；‎ ‎（2）设点P1（m,y1）、P2（m+1,y2）、P3(m+2,y3)在这个二次函数的图像上．‎ ‎①当m=4时，y1、y2、y3能否作为同一个三角形的三边的长？请说明理由；‎ ‎②当m取不小于5的任意实数时，y1、y2、y3一定能作为同一个三角形三边的长，请说明理由．‎ ‎【答案】解：（1）把点P代入二次函数解析式得5= （－2）2－2b－3，解得b=－2.‎ 当1＜x≤3时y的取值范围为－4＜y≤0.‎ ‎（2）①m=4时，y1、y2、y3的值分别为5、12、21，由于5+12＜21，不能成为三角形的三边长．‎ ‎②当m取不小于5的任意实数时，y1、y2、y3的值分别为m2－2m－3、m2－4、m2＋2m－3，由于， m2－2m－3＋m2－4＞m2＋2m－3，（m－2）2－8＞0，‎ 当m不小于5时成立，即y1＋y2＞y3成立．‎ 所以当m取不小于5的任意实数时，y1、y2、y3一定能作为同一个三角形三边的长，‎ ‎4. （2013广东汕头，15，6分）已知抛物线与x轴有交点．‎ ‎ (1)求c的取值范围；‎ ‎(2)试确定直线y＝cx+l经过的象限，并说明理由．‎ ‎【答案】（1）∵抛物线与x轴没有交点 ‎∴⊿＜0，即1－2c＜0‎ 解得c＞‎ ‎(2)∵c＞‎ ‎∴直线y=x＋1随x的增大而增大，‎ ‎∵b=1‎ ‎∴直线y=x＋1经过第一、二、三象限 ‎5. （2013湖南怀化，22，10分）已知：关于x的方程 （1） 当a取何值时，二次函数的对称轴是x=-2；‎ （2） 求证：a取任何实数时，方程总有实数根.‎ ‎【答案】‎ ‎(1)解：∵二次函数的对称轴是x=-2‎ ‎∴ ‎ 解得a=-1‎ 经检验a=-1是原分式方程的解.‎ 所以a=-1时，二次函数的对称轴是x=-2；‎ ‎（2）1）当a=0时，原方程变为-x-1=0，方程的解为x= -1；‎ ‎ 2）当a≠0时，原方程为一元二次方程，，‎ 当方程总有实数根，‎ ‎∴‎ 整理得，‎ ‎∵a≠0时 总成立 所以a取任何实数时，方程总有实数根.‎ ‎6. (2013江苏南京，24，7分)（7分）已知函数y=mx2－6x＋1（m是常数）．‎ ‎⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；‎ ‎⑵若该函数的图象与x轴只有一个交点，求m的值．‎ ‎【答案】解：⑴当x=0时，．‎ 所以不论为何值，函数的图象经过轴上的一个定点（0，1）．‎ ‎⑵①当时，函数的图象与轴只有一个交点；‎ ‎②当时，若函数的图象与轴只有一个交点，则方程有两个相等的实数根，所以，． ‎ 综上，若函数的图象与轴只有一个交点，则的值为0或9．‎ ‎10．（2013四川绵阳24，12）已知抛物线:y=x²-2x+m-1 与x轴只有一个交点，且与y轴交于A点,‎ 如图，设它的顶点为B ‎(1)求m的值；‎ ‎(2)过A作x轴的平行线，交抛物线于点C，求证是△ABC是等腰直角三角形；‎ ‎(3)将此抛物线向下平移4个单位后，得到抛物线C'，且与x 轴的左半轴交于E点，与y轴交于F点，如图.请在抛物线C'上求点P，使得△EFP是以EF为直角边的直角三角形. ‎ ‎【答案】（1）抛物线与x轴只有一个交点，说明△=0，∴m=2‎ ‎（2）∵抛物线的解析式是y=x²-2x+1,∴A（0，1），B（1，0）∴△AOB是等腰直角三角形，又AC∥OB,∴∠BAC=∠OAB=45°A，C是对称点，∴AB=BC，∴△ABC是等腰直角三角形。‎ ‎（3）平移后解析式为y=x²-2x-3,可知E(-1,0),F(0,-3)∴EF的解析式为：y=-3x-3,平面内互相垂直的两条直线的k值相乘=-1，所以过E点或F点的直线为y=x+b把E点和F点分别代入可得b=或-3，∴y=x+或y=x-3列方程得解方程x1=-1,x2=, x1 是E点坐标舍去，把x2=代入得y=,∴P1（，）同理易得x1 = 0舍去，x2= 代入y=-,∴P2(,-)‎ ‎11. （2013贵州贵阳，21，10分）‎ 如图所示，二次函数y=-x2+2x+m的图象与x轴的一个交点为A（3，0），另一个交点为B，且与y轴交于点C．‎ ‎（1）求m的值；（3分）‎ ‎（2）求点B的坐标；（3分） ‎ ‎（3）该二次函数图象上有一点D（x，y）（其中x＞0，y＞0），使S△ABD=S△ABC，求点D的坐标．（4分）‎ ‎（第21题图）‎ ‎【答案】解：（1）将（3，0）代入二次函数解析式，得 ‎-32+2×3+m=0．‎ 解得，m=3．‎ ‎（2）二次函数解析式为y=-x2+2x+3，令y=0，得 ‎-x2+2x+3=0．‎ 解得x=3或x=-1．‎ ‎∴点B的坐标为（-1，0）．‎ ‎（3）∵S△ABD=S△ABC，点D在第一象限，‎ ‎∴点C、D关于二次函数对称轴对称．‎ ‎∵由二次函数解析式可得其对称轴为x=1，点C的坐标为（0，3），‎ ‎∴点D的坐标为（2，3）．‎ ‎12. （2013广东省，15，6分）已知抛物线与x轴有交点．‎ ‎ (1)求c的取值范围；‎ ‎(2)试确定直线y＝cx+l经过的象限，并说明理由．‎ ‎【答案】（1）∵抛物线与x轴没有交点 ‎∴⊿＜0，即1－2c＜0‎ 解得c＞‎ ‎(2)∵c＞‎ ‎∴直线y=x＋1随x的增大而增大，‎ ‎∵b=1‎ ‎∴直线y=x＋1经过第一、二、三象限 ‎13. （2013广东肇庆，25，10分）已知抛物线（>0）与轴交于、两点．‎ ‎（1）求证：抛物线的对称轴在轴的左侧；‎ ‎（2）若（是坐标原点），求抛物线的解析式；‎ ‎（3）设抛物线与轴交于点，若D是直角三角形，求D的面积．‎ ‎【答案】（1）证明：∵>0 ∴ ‎ ‎ ∴抛物线的对称轴在轴的左侧 ‎ ‎（2）解：设抛物线与轴交点坐标为A（，0），B（，0），‎ 则， ， ∴与异号 ‎ 又 ∴ 由（1）知：抛物线的对称轴在轴的左侧 ‎∴， ∴, ‎ 代入得：‎ 即，从而，解得： ‎ ‎∴抛物线的解析式是 ‎ ‎（3）[解法一]：当时， ∴抛物线与轴交点坐标为（0，）‎ ‎∵D是直角三角形，且只能有AC⊥BC，又OC⊥AB，‎ ‎∴∠CAB＝ 90°— ∠ABC，∠BCO＝ 90°— ∠ABC，∴∠CAB ＝∠BCO ‎∴Rt△AOC∽Rt△COB， ‎ ‎∴，即 ∴ ‎ ‎ 即 解得： ‎ 此时＝ ，∴点的坐标为（0，—1）∴OC＝1‎ 又 ‎ ‎∵>0，∴ 即AB＝ ∴D的面积＝×AB×OC＝´´1＝‎ ‎[解法二]：略解: 当时， ∴点（0，）‎ ‎∵D是直角三角形 ∴ ‎ ‎∴ ‎ ‎∴ ∴ ‎ 解得： ‎ ‎∴‎ ‎14. （2013江苏盐城，23，10分）已知二次函数y = - x2 - x + .‎ ‎（1）在给定的直角坐标系中，画出这个函数的图象；‎ ‎（2）根据图象，写出当y ＜ 0时，x的取值范围；‎ ‎（3）若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式．‎ ‎【答案】（1）画图(如图)； ‎ ‎ （2）当y ＜ 0时，x的取值范围是x＜-3或x＞1；‎ ‎ （3）平移后图象所对应的函数关系式为y=- （x-2）2+2（或写成y=- x2+2x）.‎ ‎15. (20011江苏镇江,24,7分)如图,在△ABO中,已知点A(,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.‎ ‎(1)C点坐标为_____;‎ ‎(2)以点O为旋转中心,将△ABO顺时针旋转角a(0°0,n<0,m<0, n<0,当m<0, n<0时，由一次函数的性质可得其图象过第二、三、四象限.‎ ‎【答案】C.‎ ‎【点评】由二次函数的图象可确定其顶点坐标的符号；一次函数图象的性质：当k>o,b>o时，一次函数y=kx+b过一、二、三象限；当k>o,bo时，一次函数y=kx+b过一、二、四象限；当k0 B.a+b=‎0 C.2b+c>0 D‎.4a十c<2b 解析：观察图形知，抛物线的开口方向向上，a＞0,对称轴是直线x=-,代人对称轴公式得：a=b,所以b＞0,抛物线与y轴交点在负半轴上，故c＜0,由此可知A项和B项错误，观察图形，当x=1时，对应点的纵坐标为负，代入函数得，a+b+c＜0,即2b+c＜0,知C项错误。观察图形，横轴上的数字1所在位置介于对称轴和抛物线与x轴的交点之间，根据对称性，横轴上的数字2应介于对称轴和与抛物线另一交点之间，即当x=2时，函数值为负，代人函数式得，4a-2b+c＜0,故D项正确。‎ 答案：D 点评：此类问题通常做法是：一观察图形，所有条件在图形中找，二了解抛物线的性质。‎ ‎（2012浙江省衢州，10，3分）已知二次函数y＝－x 2－7x＋，若自变量x分别取x1，x2，x3，且0＜x1＜x2＜x3，则对应的函数值y1，y2，y3的大小关系正确的是( )‎ A.y1＞y2＞y3 B. y1＜y2＜y‎3 ‎ C.y2＞y3＞y1 D. y2＜y3＜y1‎ ‎【解析】因为a=－<0，此二次函数的开口方向向下，又y＝－x 2－7x＋＝－( x+7) 2＋32，抛物线的对称轴为x=-7，当x＞0＞-7时，y随x的增大而减少，故y1＞y2＞y3．‎ ‎【答案】A ‎【点评】主要考查了二次函数的图象性质及单调性的规律，解决此类问题的方法一般是：先确定抛物线的对称轴及开口方向，再根据点与对称轴的远近，判断函数值的大小．‎ ‎25.3 用待定系数法求二次函数关系式 ‎（2012江苏泰州市，25，本题满分10分）如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上，二次函数y=的图像经过B、C两点．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）结合函数的图像探索：当y>0时x的取值范围．‎ ‎ （第25题图）‎ ‎【解析】用待定系数法将已知两点的坐标代入二次函数解析式，即可求出b，c的值，然后通过解一元二次方程求抛物线与x轴的交点坐标，由图象法求得函数值y为正数时，自变量x的取值范围．‎ ‎【答案】由题意可得：B（2,2），C（0,2），将B、C坐标代入y=得：c=2，b=，所以二次函数的解析式是y=x2+x+2‎ ‎(2) 解x2+x+2=0，得：x1=3，x2=-1，由图像可知：y>0时x的取值范围是-1＜x＜3‎ ‎【点评】本题考查了二次函数解析式的求法及利用图象法求解一元二次不等式，渗透了数形结合思想．其中本题的解法将三个“二次”和谐地结合起来，突显二次函数的纽带作用，通过函数，将方程、不等式进行了综合考查．‎ ‎25.4　用函数观点看一元二次方程 ‎ ‎（2012山东泰安，10，3分）二次函数的图象如图，若一元二次方程有实数根，则m的最大值为（ ）‎ A.-3 B‎.3 C.-5 D.9 ‎ ‎【解析】方法一：图象法，由得，一元二次方程有实数根有实数根，得函数与函数y=-m有交点，所以-m≥-3,m≤3;‎ 方法二：因为一元二次方程有实数根，所以b2-4am≥0,由 的图象可得顶点纵坐标，，b2=12a,所以12a-4am≥0,解得m≤3.‎ ‎【答案】B.‎ ‎【点评】本题考查了二次函数的图象与一元二次方程的根之间的关系，既可以用图象法，也可以用算术法，开拓了学生的思维。‎ ‎（2012四川省资阳市，9，3分）如图是二次函数的部分图象，由图象可知不等式的解集是 A． B． C． D．‎ ‎（第9题图）‎ y x ‎【解析】由二次函数的对称性，在已知了对称轴直线和与x轴的一个交点坐标（5，0）即可得出另一个交点坐标（-1，0）；再由不等式的解集即指x轴下方图像所对应的x取值.故选D.‎ ‎【答案】D ‎【点评】本题主要考查了函数图象与不等式之间的关系，利用数形结合思想不难选出D选项，但本题如果对数形结合思想的不理解或不能熟练运用，有可能会采取代入对称轴直线及与x轴交点坐标的方法运算，将会花去考生大量时间，故解决本题的关键是熟练初中数学的常见数学思想方法.难度中等.‎ ‎（2012年四川省德阳市，第12题、3分．）设二次函数，当时，总有，当时，总有，那么的取值范围是 A. B. C. D.‎ ‎【解析】∵二次函数，当时，总有，当时，总有；∴解得 b=-4,c=3. ‎ ‎【答案】A ‎【点评】本题考查的是抛物线与x轴的交点问题，根据题意得出二次函数的交点情况得出关于b,c的方程组是解决此题的关键．‎ ‎（2012浙江省温州市，24，14分）如图，经过原点的抛物线与 轴的另一个交点为A。过点作直线轴于点M，交抛物线于点B。记点B关于抛物线对称轴的对称点为C（B、C不重合）。连结CB,CP。‎ ‎（1）当时，求点A的坐标及BC的长；‎ ‎（2）当时，连结CA，问为何值时？‎ ‎（3）过点P作且，问是否存在，使得点E落在坐标轴上？若存在，求出所有满足要求的的值，并定出相对应的点E坐标；若不存在，请说明理由。‎ ‎【解析】(1) 当m=3时，易得；分别令y=0，x=1 易得A、B的坐标．.由B，C关于对称轴对称，易得BC=4．(2)构造相似三角形，可算出m值。（3）分情况讨论点E在x轴上或y轴上．‎ ‎【答案】解：（1）当m=3时，，‎ 令y=0，得，∴∴A(6，0)‎ 当x=1时，y=5，∴B（1，5）‎ ‎∵抛物线的对称轴为直线x=3，‎ 又∵B，C关于对称轴对称，∴BC=4．‎ ‎（2）过点C作CH⊥x轴于点H（如图1），‎ 由已知得∠ACP=∠BCH=90°，‎ ‎∴∠ACH=∠PCB,‎ 又∵∠AHC=∠PBC=90°，‎ ‎∴△ACH∽△PCB，∴．‎ ‎∵抛物线的对称轴为直线x=m，其中m>1，‎ 又∵B,C关于对称轴对称，‎ ‎∴，‎ ‎∴‎ ‎∴‎ 又∵‎ ‎∴,‎ ‎∴‎ ‎∴∴．‎ ‎（3）∵B，C不重合，∴m≠1．‎ ‎（I）当m＞1时，BC=2(m-1),PM=m,‎ BP=m-1.‎ ‎(i)若点E在x轴上（如图1），‎ ‎∵∠CPE=90°，∴∠MPE＋∠BPC=∠MPE＋∠MEP=90°，‎ ‎∴∠BPC=∠MEP．‎ 又∵∠CPB=∠PME=90°，PC=EP ‎∴△BPC≌△MEP，∴BC=PM,‎ ‎∴2（m－1）=m，‎ ‎∴m=2,此时点E的坐标是（2，0）．‎ ‎（II）当0＜m＜1时，BC=2（1－m），PM=m，‎ BP=1－m,‎ ‎(i)若点E在x轴上（如图3），‎ 易证△BPC≌△MEP，∴BC=PM，‎ ‎∴2（1－m）=m,∴，此时点E的坐标是．‎ ‎（ii）若点E在y轴上（如图4），‎ 过点P作PN⊥y轴于点N，易证△BPC≌△NPE，∴BP=NP=OM=1,‎ ‎∴1－m=1，∴m=0（舍去）．‎ 综上所述，当m=2时，点E的坐标是（2，0）或（0，4）；‎ 当时，点E的坐标是．‎ ‎【点评】本题以二次函数图象为载体，结合一元二次方程、相似三角形与全等问题；考查了初中数学的主要知识：函数与方程，考查了学生综合运用数学知识以及运用转化思想、数形结合思想、函数与方程思想解决问题的能力，.试题由易到难，层层递进，具有一定的梯度，难度较大.‎ ‎（2012江苏省无锡市，24，8′）如图，在边长为‎24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方形形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）。已知E、F在ＡＢ边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).‎ ‎（1）若折成的包装盒恰好是个正方形，试求这个包装盒的体积V；‎ ‎（2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？‎ ‎【解析】（1）根据折叠前后图形特点，若折成的包装盒恰好是个正方形，则这包装盒的长、宽、高相等，利用等腰直角三角形的性质，可以用x形式表示出AE、EF、BF的长度，再利用正方形ABCD的边长为24cm，构造有关x的方程，进一步求出其值。正方形的体积公式：其中 表示正方形的边长。（2）用利用等腰直角三角形的性质，可以用x形式表示出AE、EF、BF的长度，进一步求出包装盒的表面（不含下底面）积，利用二次函数的知识求其最值。‎ ‎【答案】解：（1）根据题意，知这个正方形的底面边长 ‎ ∴∴‎ ‎ ∴‎ 1. 设包装盒的底面边长为，高为hcm,则 ‎ ∴‎ ‎ ∵∴当时，S取得最大值‎384cm²‎ ‎【点评】本题利用折叠考查了学生的空间想象能力，用x形式正确表示出相关线段的长度，进一步求出相关的体积和面积表达形式，利用二次函数求代数式的最值，把平面几何与代数的知识柔和在一起，难度属于中等偏上。‎ ‎（2012山东省潍坊市，题号23，分值10）许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题。某款燃气灶旋钮位置从0度到90度（如图），燃气关闭时，燃气关闭时，燃气灶旋钮的位置为0度，旋钮角度越大，燃气流量越大，燃气开到最大时，旋钮角度为90度.为测试燃气灶旋钮在不同位置上的燃气用量，在相同条件下，选择在燃气灶旋钮的5个不同位置上分别烧开一壶水（当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度度的范围是），记录相关数据得到下表：‎ 旋钮角度（度）‎ ‎20‎ ‎50‎ ‎70‎ ‎80‎ ‎90‎ 所用燃气量（升）‎ ‎73‎ ‎67‎ ‎83‎ ‎97‎ ‎115‎ ‎（1）请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律？‎ ‎（2）当旋钮角为多少时，烧开一壶水所用燃气量最少？最少是多少？‎ ‎（3）某家庭使用此燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气用量.‎ 考点：一次函数、反比例函数、二次函数的判别，二次函数的最值计算.‎ 解答：（1）若设，由，解得 所以，把代入得，所以不符合 1分 ‎ 若设，由解得所以 把代入得，所以不符合 2分 若设，则由，解得 所以 4分 把代入得，把代入得，符合题意 所以选用二次函数能表示所用燃气量y升与旋钮角度x度的变化规律 5分 ‎(2)由（1）得 所以当时, y取得最小值65‎ 即当旋钮角度为40度时，烧开一壶水所用燃气量最少，最少为65升. ‎ ‎（3）由(2)及表格知采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气 ‎115－65=‎50升 ‎ 设该家庭以前每月平均用气量为a立方米，则由题意得 解得a=23（立方米）‎ 即该家庭以前每月平均用气量为23立方米 ‎ 点评：本题考查了实际问题中函数类型的判定，二次函数的最值计算。解决此类问题的关键在于根据题目中提供的信息，建立适当的函数模型，从而求解。‎ ‎（湖南株洲市10,24题）如图，一次函数分别交y轴、x 轴于A、B两点，抛物线过A、B两点。‎ ‎（1）求这个抛物线的解析式；‎ ‎（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N。求当t 取何值时，MN有最大值？最大值是多少？‎ ‎（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标。‎ ‎【解析】（1）根据一次函数的解析及两坐标轴交点坐标，求出二次函数的解析式；（2）根据M、N所处的位置用含有t的代数表示出M、N的坐标，利用MN在直线 x=t，求出MN的长，根据ｔ的取值确定MN的最大值；（3）利用平行四边形的对边平行且相等的方法确定D点的坐标.‎ ‎【解】（1）易得A（0，2），B（4，0） ……… 1分 将x=0,y=2代入 ………2 分 将x=4,y=0代入 ‎ ‎ ……… 3分 ‎（2）由题意易得 ……… 4分 ‎ ……… 5分 当 ………6 分 ‎ ‎（3）、由题意可知，D的可能位置有如图三种情形 ‎……… 7分 当D在y轴上时，设D的坐标为（0，a）‎ 由AD=MN得，‎ 从而D为（0，6）或D（0，-2） ……… 8分 当D不在y轴上时，由图可知 易得 由两方程联立解得D为（4，4） ……… 9分 ‎ 故所求的D为（0，6），（0，-2）或（4，4） … 10分 ‎【点评】求解析式的关键是确定图象上点的坐标，点坐标的确定关键要看题中的所给的条件适合哪种方法.‎ ‎（2012山东省潍坊市，题号24，分值11）24、 (本题满分11分)如图，已知抛物线与坐标轴分别交于A、B、C三点，过坐标原点O的直线与抛物线交于M、N两点.分别过点C、D作平行于轴的直线、.‎ ‎（1）求抛物线对应的二次函数的解析式；‎ ‎（2）求证以ON为直径的圆与直线相切；‎ ‎（3）求线段MN的长（用表示），并证明M、N两点到直线的距离之和等于线段MN的长。‎ 考点：本题考察了二次函数的知识、直线与圆的位置关系、勾股定理、一元二次方程等知识。‎ 解答：（1）设抛物线对应二次函数的解析式为 由 ，解得，所以 ‎ ‎（2）设，因为点M、N在抛物线上，‎ 所以，，所以；‎ 又=，所以ON=，又因为，‎ 所以ON ‎ ‎ 设ON的中点为E，分别过点Ｎ、Ｅ向直线作垂线，垂足分别为P、F，‎ 则 所以ON=2EF，‎ 即ON的中点到直线的距离等于ON长度的一半，‎ 所以以ON为直径的圆与直线相切。 7分 ‎（3）过点M作MH⊥NP交NP于点H，则 又，所以 所以；‎ 又因为点M、N既在的图象上，又在抛物线上，所以，即，‎ 所以，‎ 所以，‎ 所以 所以 ‎ 延长NP交于点Ｑ，过点Ｍ作ＭＳ⊥交于点S，‎ 则MS+NQ=‎ 又=‎ 所以MS+NQ=‎ 即MN两点到距离之和等于线段MN的长.‎ 点评：本题考察了二次函数的知识、直线与圆的位置关系、勾股定理、一元二次方程等知识，综合性较强。‎ ‎2012年全国各地中考数学模拟试卷分类汇编 ‎　二次函数 一、选择题 ‎1、（2012年浙江五模）抛物线的对称轴是（ ）‎ A．直线x=－2　 B．直线 x=‎2 C．直线x=－3 D．直线x=3‎ 答案：C ‎2、（2012年浙江五模）将抛物线向上平移若干个单位，使抛物线与坐标轴有三个交点，如果这些交点能构成直角三角形，那么平移的距离为（ ）‎ ‎ A．个单位 B．1个单位 C．个单位 D．个单位 答案：A ‎3、（2012年浙江一模）抛物线先向右平移1个单位，再向上平移3个单位，得到新的抛物线解析式是（ ）‎ A． B． ‎ C． 　 D．‎ 答案：D 第4题 ‎4、（2012年重庆外国语学校九年级第二学期期中）已知抛物线在平面直角坐标系中的位置如图所示，‎ A、 B、 ‎ ‎ C、 D、 ‎ 答案：D ‎5、（保沙中学2012二模）已知二次函数的图象过点A（1，2），B ‎（3，2），C（5，7）．若点M（-2，y1），N（-1，y2），K（8，y3）也在二次函数的图象上，则下列结论正确的是（） ‎ A．y1＜y2＜y3 B．y2＜y1＜y3 C．y3＜y1＜y2 D．y1＜y3＜y2 ‎ 答案：C ‎6、（广东省2012初中学业水平模拟六）二次函数 y＝ax2-ax＋1 (a≠0)的图象与x轴有两个交点，其中一个交点为(,0),那么另一个交点坐标为（ ） ‎ A．(, 0) B． (, 0) C． (, 0) D．(,0)‎ 答案：D ‎7、（广东省2012初中学业水平模拟一）抛物线的顶点坐标为( ). ‎ A．（，） B．（，） C．（，） D．（，）‎ 答案；D ‎8、（广东省2012初中学业水平模拟一）函数是关于的二次函数，则( ). ‎ A．等于1 B．不等于1 C．等于 D．不等于 答案：B ‎9、（广州海珠区2012毕业班综合调研）若二次函数的解析式为，则其函数图象与轴交点的情况是（ ）‎ A．没有交点 B．有一个交点 ‎ C．有两个交点 D．无法确定 答案：A ‎10、（2012江苏无锡前洲中学模拟）如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（　 　）‎ A． B． C． D．‎ ‎(第1题)‎ A B C D 答案：B ‎11.（2012荆门东宝区模拟）在同一直角坐标系中，函数y＝mx+m和函数y＝－mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）．‎ ‎(第2题)‎ 答案：D ‎12. （2012鄂州市梁子湖区模拟） 如图，等腰梯形ABCD的底边AD在轴上，顶点C在轴正半轴上，B（4,2），一次函数的图象平分它的面积，关于的函数的图象与坐标轴只有两个交点，则的值为（ D ）. ‎ A．0 B． C．－1 D．0或或－1‎ 第3题图 答案：D ‎13、(2012广西钦州市模拟)函数（为常数）的图象与轴的交点有 ‎（A）0个 （B）1个 （C）2个 （D）1个或2个 答案：D ‎14、(2012广西北海市模拟)抛物线的顶点坐标是·······························（ ）‎ ‎ A.（1，3） B.（-1，3） C.（1，-3） D.（-1，-3）‎ 答案：B ‎15、(2012广西北海市模拟)函数与的图象可能是·················（ ）‎ A B D ‎1‎ O ‎1‎ O ‎1‎ O ‎1‎ O C 答案：C ‎16、(2012广西北海市模拟)已知二次函数的图象如图（2）所示，则下面结论成立的是（ ）‎ ‎ A.， B.， C.， D.，‎ 答案：C 第8题 ‎17、(2012广西北海市模拟)．如图(4)， 的半径为2，是函数的图象， 是函数的 图象，则阴影部分的面积是 .‎ 答案：‎ ‎18、（2012江苏江阴市澄东一模 ）若二次函数．当≤l时，随的增大而减小，则的取值范围是（ ） ‎ ‎ A．=l B．>l C．≥l D．≤l 答案：C ‎19、（2012江苏江阴市澄东一模 ）二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是（ ）.‎ 答案：D ‎20、（2012年山东东营一模）如果二次函数（a＞0）的顶点在x轴上方，那么（ ）‎ A，b2－‎4ac≥0 B，b2－‎4ac＜‎0 ‎‎ C，b2－‎4ac＞0 D，b2－‎4ac＝0‎ 答案：B ‎21、（2012年济宁模拟）已知二次函数y=-x2+x-15，当自变量x取m时对应的值大于0，当自变量x分别取m-1、m+1时对应的函数值为y1、y2，则y1、y2必须满足（　　）‎ A.y1＞0、y2＞0 B.y1＜0、y2＜‎0 C.y1＜0、y2＞0 D.y1＞0、y2＜0‎ 答案：B ‎22.、（2012年山东潍坊二模）已知二次函数(如图)y=3(x-1)2+k的图象上有三个点 A(,y1),B(2,y2),C(,y3),则y1、y2、y3的大小关系为 A.y1>y2>y3； B.y2>y3>y1； ‎ C.y3>y1>y2； D.y3>y2>y1‎ 答案：D ‎23、‎ ‎（2012年山东潍坊二模）已知二次函数(如图)y=3(x-1)2+k的图象上有三个点A(,y1),B(2,y2),C(,y3),则y1、y2、y3的大小关系为 A.y1>y2>y3； B.y2>y3>y1； ‎ C.y3>y1>y2； D.y3>y2>y1‎ 答案：D ‎24、2012年山东潍坊二模）已知二次函数y=x2－bx+1（－1≤b≤1），当b从－1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动。下列关于抛物线的顶点位置的描述中，正确的是 ‎ A．先往左上方移动，再往左下方移动 ‎ B．先往左下方移动，再往左上方移动 ‎ ‎ C．先往右上方移动，再往右下方移动 ‎ ‎ D．先往右下方移动，再往右上方移动 答案：C ‎25、2012四川夹江县模拟）已知抛物线在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（ ）‎ A． B． ‎ C． D．‎ ‎_‎ x ‎_‎ y ‎_‎ O ‎_‎ ‎1‎ ‎ ‎ ‎_‎ ‎?‎ ‎7‎ ‎??‎ ‎ ‎ 答案：D ‎26、（2012四川沙湾区调研）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为 答案：D ‎27、(2012年杭州一模)若函数与函数的图象如左下图所示，则函数的大致图象为（ ）‎ 答案： D ‎28、(2012年河北一模)抛物线的顶点坐标是（ ）‎ A、（2，0） B、（－2，0） C、（0，2） D、（0，－2）‎ 答案：Ｂ ‎29、(2012年荆州模拟)已知函数y=（k－3）x2＋2x＋1的图像与x轴有交点，则k的取值范围为 ‎ A、k<4 B、k≤‎4 C、k<4且k≠3 D、k≤4且k≠3 ‎ 答案： B ‎30、(2012年荆州模拟)已知函数，则使y=k成立的x值恰好有三个，则k的值为 A．0 B．‎1 ‎‎ ‎ C．2 D．3‎ 答案： D ‎31、(2012年江阴模拟)若二次函数．当≤l时，随的增大而减小，则 的取值范围是（ ） ‎ ‎ A．=l B．>l C．≥l D．≤l 答案： C ‎32、(2012年江阴模拟)二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是（ ）.‎ 答案： D ‎33、（2012北京市石景山区初三一模）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点P以每秒一个单位的速度沿着B—C—A运动，⊙P始终与AB相切，设点P运动的时间为t，⊙P的面积为y，则y与t之间的函数关系图像大致是（ ）‎ ‎ ‎°‎ ‎°‎ ‎°‎ ‎°‎ ‎°‎ ‎°‎ ‎°‎ ‎．‎ t O ‎ y O ‎ y O ‎ y t O ‎ y t ‎ t ‎ A B C D 答案：B ‎34、（2013—2012学年第二学期昌平区初三年级第一次统一练习）如图，已知□ABCD中，AB=4,AD=2,E是AB边上的一动点（与点A、B不重合），设AE=,DE的延长线交CB的延长线于点F，设BF=，则下列图象能正确反映与的函数关系的是（ ）‎ 答案：B A．‎ ‎16‎ ‎9‎ ‎5‎ ‎8‎ O y ‎35、[2012年南长区模拟考试数学试题卷]如图，在Rt△ABC中，∠C=90°，AB=‎5cm，BC=‎3cm，动点P从点A 出发，以每秒‎1cm的速度，沿A→B→C的方向运动，到达点C时停止．设y=PC2，运动时间为t秒，则能反映y与t之间函数关系的大致图象是 【 ▲ 】‎ D．‎ ‎16‎ ‎5‎ ‎9‎ ‎8‎ C．‎ O ‎9‎ ‎16‎ ‎5‎ ‎8‎ B．‎ ‎8‎ O ‎9‎ ‎16‎ ‎5‎ 第10题 A B C P ‎·‎ ‎8‎ 答案：A ‎36、（2012江苏江阴华士片九年级下期中检测，9,3分）下列二次函数中，图象以直线x=2为对称轴、且经过点(0，1)的是 ( )‎ ‎ A．y=(x－2)2+1 B．y=(x+2)2+1[来~源^*:&中教%网]‎ ‎ C．y=(x－2)2－3 D．y=(x+2)2－3‎ 答案：C ‎37、（2012江苏无锡前洲中学模拟）如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（　 　）‎ A． B． C． D．‎ ‎(第1题)‎ A B C D 答案：B ‎38.（2012荆门东宝区模拟）在同一直角坐标系中，函数y＝mx+m和函数y＝－mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）．‎ ‎(第2题)‎ 答案：D ‎39. (2012浙江椒江二中、温中联考)二次函数y=(x－3)(x＋2)的图象的对称轴是( )‎ A．x=3 B．x=－‎2 C．x= D．x= ‎ 答案：D ‎40. (2012浙江椒江二中、温中联考)现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P（x，y），那么它们各掷一次所确定的点P落在已知抛物线y＝－x2+4x上的概率为（ ）‎ A.错误！嵌入对象无效。 　　 B.错误！嵌入对象无效。 　C.错误！嵌入对象无效。 　　 D.错误！嵌入对象无效。 ‎ 答案：B ‎41. (2012浙江椒江二中、温中联考)若一抛物线y=ax2与四条直线x=1、x=2、y=1、y=2围成的正方形有公共点，则a的取值范围是 )‎ A. ≤a≤1 (B. ≤a≤‎2 C.≤a≤1 D. ≤a≤2 ‎ 答案：D ‎42 (2012年浙江省嵊州市评价)如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB以相同间隔‎0.2米用5‎ 第6题 根立柱加固，拱高OC为‎0.36米，则立柱EF的长为（ ▲ ） ‎ ‎ A．‎0.4米 B．‎0.16米 ‎ C．‎0.2米 D．‎0.24米 ‎ 答案：C ‎43、（2012 内蒙古呼伦贝尔一摸）已知二次函数的图象过点A（1，2），B（3，2），C（5，7）．若点M（-2，y1），N（-1，y2），K（8，y3）也在二次函数的图象上，则下列结论正确的是（） ‎ A．y1＜y2＜y3 B．y2＜y1＜y3 C．y3＜y1＜y2 D．y1＜y3＜y2 ‎ 答案：B ‎44．(2012宁德市一摸)抛物线的对称轴方程是（ ）‎ A． B． C． D．‎ ‎45．（2012江苏省无锡市期中）若二次函数，当分别取、两个不同的值时，函数值相等，则当取时，函数值为 （ ） ‎ A. B. C. D. ‎ 答案：‎ ‎46、（2012年北京市朝阳区）已知关于的一元二次方程的两个实数根分别为，（），则二次函数中，当时，的取值范围是 A． B． C． D．或 答案：C ‎ ‎47．（2012大连市模拟题）如图2，一条抛物线与x轴相交于A、B两点（点A在点B的 左侧），其顶点P在线段MN上移动．若点M、N的坐标分别 为（－1，－2）、（1，－2），点B的横坐标的最大值为3，‎ 则点A的横坐标的最小值为 A．－3 B．－‎1 ‎‎ ‎ C．1 D．3‎ 答案：A 二、填空题 ‎1、（2012年浙江金华模拟）如图，已知函数 与y=ax2+bx（a<0，b>0）的图象交于点，点的纵坐标为－１，则关于的方程的解为▲．‎ 第2题图 答案：x=3‎ ‎2、（2012年浙江绍兴八校自测模拟）如图所示，P是边长为1的正三角形ABC的BC边上一点，从P向AB作垂线PQ，Q为垂足．延长QP与AC的延长线交于R，设BP=x（0≤x≤1），△BPQ与△CPR的面积之和为y，把y表示为x的函数是____________________________． ‎ ‎ 答案： ‎ ‎3、（2012年浙江绍兴八校自测模拟）若关于的二次函数的图象与端点在，和，）的线段只有一个交点，则的取值范围是___________________________．‎ 答案：‎ ‎4、（2012年浙江绍兴县一模）已知A、B是抛物线y=x2－4x+3上关于对称轴对称的两点，则A、B 的坐标可能是 .（写出一对即可）‎ 答案：不唯一，如：(3，-1)，(1，-1)‎ ‎5、（广东省2012初中学业水平模拟三）已知二次函数错误！不能通过编辑域代码创建对象。．‎ ‎⑴求证：无论错误！不能通过编辑域代码创建对象。取何实数，此二次函数的图像与错误！不能通过编辑域代码创建对象。轴都有两个交点；‎ ‎⑵若此二次函数图像的对称轴为错误！不能通过编辑域代码创建对象。，求它的解析式；‎ 答案（1）证明：令y=0, 则, ‎ ‎∵△=‎ ‎ =‎ ‎ =‎ ‎ ∵ ≥0, ∴＞0‎ ‎∴无论错误！不能通过编辑域代码创建对象。取何实数，此二次函数的图像与错误！不能通过编辑域代码创建对象。轴都有两个交点. -------------4分 ‎(2).∵对称轴为x=，‎ ‎∴k=2 ∴解析式为 ---------7分 ‎：‎ ‎6、(2012江西高安一模)抛物线 y=x2+2x-3的顶点坐标为 ．‎ 答案：(-1,-4) ‎ ‎7、(2012广西北海市模拟)．若，为二次函数的图象上的三点，则，，的大小关系是 .（用“”号连接）‎ 答案：‎ ‎8、（2012年山东东营一模）已知二次函数y=ax2+bx+c的图象与x轴交于A(1，0)，B(3，0)两点，与y轴交于点C (0，3)，则二次函数的解析式是__________________‎ 答案：y=x2－4x+3‎ ‎9、（2012年济宁模拟）将y=2x2－12x－12变为y=a（x－m）2+n的形式，则m•n=　_________　．‎ 答案：-90‎ ‎10、(2012年荆州模拟)直线y = 2x＋b右移3个单位长度后过抛物线y = 2x2－2x＋4的顶点，则b = 。‎ 答案： 17/2 ‎ ‎11、（2012南京江宁区九年级调研卷）把抛物线向左平移3个单位，再向下平移2个单位，所得抛物线的函数关系式为 ▲ ．‎ 答案：y=－(x+3)2－2‎ ‎12、[2012年南长区模拟考试数学试题卷]抛物线y=－x2+x－4的对称轴是 ▲ ．‎ 答案：x＝2‎ ‎13、（2012江苏江阴青阳九年级下期中检测，18,2分）如图，已知二次函数y1＝ax2＋bx＋‎ c与一次函数y2＝kx＋m的图 [中^国*%教#育出版网&]‎ 象相交于 A（－2，4）、B（8，2）两点，则能使关于x的不等式 ‎ x ‎ y O 第18题 A B ax2＋(b－k)x＋c－m＞0 成立的x的取值范围是______．[中国#~^%教育出版网*]‎ 答案：x＜-2或x＞8‎ ‎14、(2012江西高安一模)抛物线 y=x2+2x-3的顶点坐标为 ．‎ 答案：(-1,-4) ‎ ‎15. （2012年犍为县五校联考）二次函数图象的顶点坐标是 ． ‎ 答案：（1，3）‎ ‎16. (2012浙江椒江二中、温中联考)二次函数y=－3x2＋6x＋9的图象的开口方向______，它与y轴的交点坐标是______。‎ 答案：向下，（0，9）‎ ‎17.(2012年浙江省嵊州市评价)如图，已知抛物线，与轴交于A、B两点，点为抛物线的顶点。点P在抛物线的对称轴上，设⊙P的半径为，当⊙P与轴和直线BC都相切时，则圆心P的坐标为 ▲ 。 ‎ 第4题 答案：，‎ ‎18．（2012江苏省锡山区一模）抛物线y＝2(x＋1)2－2的顶点坐标为 ．‎ 答案：(-1，-2)‎ ‎19、已知抛物线的顶点坐标为（2，9），且它在x轴上截得的线段长为6，则该抛物线的解析式为 ▲ ．‎ 答案：y = −(x +1)(x −5) ‎ ‎20.如图，A1、A2、A3是抛物线（ a>0）上的三点，A1B1、A2B2、A3B3分别垂直于轴，垂足为B1、B2、B3，直线A2B2交线段A‎1A3于点C，A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为 ★ ．‎ 答案：‎ ‎21．二次函数取得最大值时，= ．‎ 答案：-‎ 三、解答题 ‎1、（2012年浙江一模）如图，在平面直角坐标系中，△ABC的A、B两个顶点在x轴上，顶点C在y轴 的负半轴上．已知OA:OB=1:5，OB=OC，△ABC的面积，抛物线 经过A、B、C三点．‎ ‎ （1）求此抛物线的函数表达式；‎ ‎（2）点P(2，－3)是抛物线对称轴上的一点，在线段OC上有一动点M，以每秒2个单 位的速度从O向C运动，（不与点O，C重合），过点M作MH∥BC，交x轴于 点H，设点M的运动时间为t秒，试把⊿PMH的面积S表示成t的函数，当t为何 值时，S有最大值，并求出最大值；‎ ‎（3）设点E是抛物线上异于点A，B的一个动点，过点E作x轴的平行线交抛物线于另 一点F. 以EF为直径画⊙Q，则在点E的运动过程中，是否存在与x轴相切的⊙Q？‎ 若存在，求出此时点E的坐标；若不存在，请说明理由．‎ 答案：‎ ‎（每小题4+6+4分，共14分）‎ ‎（1） ‎ ‎（2）由题意可求得直线BC：y=x－5，‎ ‎∵M(0，－2t) 直线MH平行于直线BC，‎ ‎∴直线MH为y=x－2t，‎ 设直线MH与对称轴交与点D，点D的坐标为（2,2－2t），‎ ‎∴DP=5－2t，‎ ‎∴ S△pmh=×2t(5－2t)=—2t2+5t (0＜t＜)，‎ 当t=时，S有最大值是． ‎ ‎（3）当点E在x轴下方且对称轴右侧时坐标为（， ）；‎ 当点E在x轴下方且对称轴左侧时坐标为（， ）；‎ 当点E在x轴上方且对称轴右侧时坐标为（， ）；‎ 当点E在x轴上方且对称轴左侧时坐标为（， ） ；‎ ‎2、（2012年浙江绍兴八校自测模拟）定义：对于抛物线y=ax2+bx+c（a、b、c是常数，a≠0），若b2=ac，则称该抛物线为黄金抛物线．例如：y=2x2－2x+2是黄金抛物线．‎ ‎（1）请再写出一个与上例不同的黄金抛物线的解析式；‎ ‎（2）若抛物线y=ax2+bx+c（a、b、c是常数，a≠0）是黄金抛物线，请探究该黄金抛物线与x轴的公共点个数的情况（要求说明理由）；‎ ‎（3）将黄金抛物线y=2x2－2x+2沿对称轴向下平移3个单位 ‎①直接写出平移后的新抛物线的解析式；‎ ‎②设①中的新抛物线与y轴交于点A，对称轴与x轴交于点B，动点Q在对称轴上，问新抛物线上是否存在点P，使以点P、Q、B为顶点的三角形与△AOB全等？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由[注：第小题可根据解题需要在备用图中画出新抛物线的示意图（画图不计分）]‎ ‎【提示：抛物线y=ax2+bx+c（a≠0）的对称轴是x=，顶点坐标是（，）】．‎ 答案：（1）如、、等.‎ ‎（2）若抛物线y=ax2+bx+c（a≠0）是黄金抛物线，则b2=ac ‎∴＝‎ 故当时，此时抛物线与x轴只有一个交点；‎ ‎ 当时，此时抛物线与x轴没有交点.‎ ‎（3）①新抛物线的解析式为；‎ ‎②存在. ‎ 有四个符合条件的点P的坐标：（0，1）、（1， －1）、（， ）、（，）.‎ ‎3、．（2012昆山一模）‎ ‎ 如图，抛物线y＝x2－x＋a与x轴交于点A、B，与y轴交于点C，其顶点在直线y　＝－2x上，‎ ‎ 　 (1)求a的值 ‎ 　 (2)求A、B两点的坐标 ‎ 　 (3)以AC、CB为一组邻边作□ABCD，则点D关于x轴的对称点D'是否在该抛物线上？请说明理由．‎ 答案：‎ ‎4、（2012年广东省深圳市实验中学一模）已知：二次函数y=ax2+bx+c（a≠0）中的x，y满足下表：‎ x ‎…‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y ‎…‎ ‎0‎ ‎﹣3‎ ‎﹣4‎ ‎﹣3‎ m ‎…‎ ‎（1）m的值为　0　；‎ ‎（2）若A（p，y1），B（p+1，y2）两点都在该函数的图象上，且p＜0，试比较y1与y2的大小．‎ 解答：解：（1）由已知表格可得 函数的对称轴为x=1，‎ ‎∴m=0；（2分）‎ ‎（2）∵p＜0，‎ ‎∴p＜p+1＜1，‎ ‎∵对称轴为x=1，‎ A、B两点位于对称轴的左侧，‎ 又因为抛物开口向上，‎ ‎∴y1＞y2．（5分）‎ 故答案为0，y1＞y2．‎ ‎5、(2012年河北一模)如图1，抛物线与x轴交于A、C两点，与y轴交于B点，与直线y=kx+b交于A、D两点．‎ ‎（1）直接写出A、C两点坐标和直线AD的解析式；‎ ‎（2）如图2，质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4．随机抛掷这枚骰子两次，把第一次着地一面的数字m记做P点的横坐标，第二次着地一面的数字n记做P点的纵坐标．则点P（m，n）落在图1中抛物线与直线围成区域内（图中阴影部分，含边界）的概率是多少？‎ ‎ ‎ 答案：‎ ‎6、（2012年北京门头沟一模）已知：关于x的一元二次方程有两个实数根.‎ ‎（1）求k的取值范围；‎ ‎（2）当k为负整数时，抛物线与x轴的交点是整数点，求抛物线的解析式；‎ ‎（3）若（2）中的抛物线与y轴交于点A，过A作x轴的平行线与抛物线交于点B，连接 OB，将抛物线向上平移n个单位，使平移后得到的抛物线的顶点落在△OAB的内部（不包括△OAB的边界），求n的取值范围.‎ 答案：解：（1）由题意得， ……………….1分 ‎ 解得，‎ ‎ K的取值范围是. ……………………..2分 ‎ （2）k为负整数，k=-2，-1.‎ ‎ 当k=-2时，与x轴的两个交点是（-1，0）（-2，0）是整数点，符合题意 …………………3分 ‎ 当k=-1时，与x轴的交点不是整数点，不符合题意 ….4分 ‎ 抛物线的解析式是 ‎ （3）由题意得，A（0，2），B（-3，2）‎ ‎ 设OB的解析式为 ‎ ,解得 ‎ OB的解析式为 ‎ 的顶点坐标是（，）‎ ‎ OB与抛物线对称轴的交点坐标（，1） …………..5分 ‎ 直线AB与抛物线对称轴的交点坐标是（，2） ………6分 ‎ 有图象可知，n的取值范围是……………………7分 ‎7、（2012年北京门头沟一模）在平面直角坐标系中，二次函数的图象与x轴交于A、 B两点（点A在点B的左侧），交y轴于点E. 点C是点A关于点B 的对称点，点F是线段BC的中点，直线l过点F且与y轴平行. 一次函数y=－x＋m的图象过点C，交y轴于D点.‎ ‎（1）求点C、点F的坐标；‎ ‎（2）点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于点G，求线段HG长度的最大值；‎ ‎（3）在直线l上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标.‎ 答案：解：（1）由题意得，A（－3，0），B（1，0） C（5，0） ………1分 ‎ F（3，0） …………………………2分 ‎（2）由题意得，，解得m=5‎ CD的解析式是 设K点的坐标是（t，0），则H点的坐标是（t，-t+5）,G点的坐标是（t，‎ ‎ K是线段AB上一动点，‎ ‎ HG=（-t+5）-（）==………..3分 ‎，‎ ‎ 当t=时，线段HG的长度有最大值是 ………………….4分 ‎（3）AC=8 ………………………5 ‎ 直线l过点F且与y轴平行，‎ ‎ 直线l的解析式是x=3.‎ ‎ 点M在l上，点N在抛物线上 ‎ 设点M的坐标是（3，m），点N的坐标是（n，）.‎ ‎ （ⅰ）若线段AC是以A、C、M、N为顶点的平行四边形的边，则须MN∥AC，MN=AC=8‎ ‎ （Ⅰ）当点N在点M的左侧时，MN=3-n ‎ 3-n=8，解得n=-5‎ ‎ N点的坐标是（-5，12）…………………6分 ‎ （Ⅱ）当点N在点M的右侧时，NM=n-3‎ ‎ n-3=8，解得n=11‎ ‎ N点坐标是（11，140） …………………..7分 ‎ （ⅱ）若线段AC是以A、C、M、N为顶点的平行四边形的对角线，由题意可知，点M与点N关于点B中心对称. 取点F关于点B的对称点P，则P点坐标是（-1，0）.过点P作NP⊥x轴，交抛物线与点N. ‎ ‎ 过点N、B作直线NB交直线l于点M.‎ ‎ ∠NBP=∠MBF,BF=BP,∠BPN=∠BFM=90°‎ ‎ △BPN≌△BFM. NB=MB ‎ 四边形ANCM是平行四边形. ‎ N点坐标是（-1，-4）………………………………….8分 ‎ 符合条件的N点坐标有（-5，12），（11，140），（-1，-4），‎ ‎8、（2012北京市石景山区初三一模）已知二次函数中，m为不小于0的整数，它的图像与x轴交于点A和点B，点A在原点左边，点B在原点右边。‎ ‎（1）求这个二次函数的解析式；‎ ‎（2）点C是抛物线与轴的交点，已知AD=AC（D在线段AB上），有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度移动，同时，另一动点Q从点C出发，以某一速度沿线段CB移动，经过t秒的移动，线段PQ被CD垂直平分，求t的值；‎ ‎（3）在（2）的情况下，求四边形ACQD的面积．‎ 答案：‎ ‎（1）∵二次函数的图像与x轴有两个交点，‎ ‎ ∴‎ ‎ ∴． ………．1分 ‎∵m为不小于0的整数，∴m取0、1． ………．2分 ‎ 当m=1时，，图像与x轴的两个交点在原点的同侧，不合题意，舍去；‎ ‎ 当m=0时，，符合题意．‎ ‎ ∴二次函数的解析式为： ………3分 ‎ （2）∵AC=AD，∴∠ADC=∠ACD ‎ ∵CD垂直平分PQ，∴DP=DQ，∴∠ADC=∠CDQ．‎ ‎ ∴∠ACD=∠CDQ，∴DQ∥AC ‎ ∴△BDQ∽△BAC，∴ ………4分 ‎ ∵AC=，BD=，AB=4．‎ ‎ ∴DQ=， ………5分 ‎∴PD=． ∴AP=AD-PD=， ‎ ‎ ∴t= ………6分 ‎ （3）∵△BDQ∽△BAC ‎∴‎ 易求，∴ ……7分 ‎∴． …8分 ‎9、（2012北京市石景山区初三一模）已知：关于的方程有两个不相等的实数根．‎ ‎（1）求的取值范围；‎ ‎（2）抛物线：与轴交于、两点．若且直线:经过点,求抛物线的函数解析式；‎ ‎（3）在（2）的条件下，直线:绕着点旋转得到直线：，设直线与轴交于点，与抛物线交于点（不与点重合），当时，求的取值范围．‎ 答案：解：（1）‎ ‎ ……………．．1分 ‎∵方程有两个不相等的实数根 ‎∴‎ ‎∴ ……………2分 （2） 抛物线中，令，则 ‎，‎ 解得：， ……………3分 ‎∴抛物线与轴的交点坐标为和 ‎∵直线:经过点 当点坐标为时，‎ 解得 当点坐标为时 ‎，‎ 解得或 ‎ ‎ ‎ 又∵‎ ‎∴且 ‎∴抛物线的解析式为；……4分 ‎（3）设 ‎①当点在点的右侧时，可证 ‎ ‎ 若，则，‎ 此时,‎ 过点的直线：的解析式 为 时 ，‎ 求得 …………5分 ‎②当点与点重合时直线与抛物线只有一个公共点 解得 令,求得 ………6分 ‎③当点在点的左侧时 可证 若，则，此时,‎ ‎，解得 ‎ 综上所述，当时错误！不能通过编辑域代码创建对象。且 ………7分 ‎10、（2012北京市延庆县初三一模）在平面直角坐标系xOy中，二次函数y1=mx2-（‎2m+3）x+m+3与x轴交于点A、点 ‎ B(点A在点B的左侧)，与y轴交于点C（其中m>0）．‎ ‎（1）求：点A、点B的坐标（含m的式子表示）；‎ ‎（2）若OB=4·AO，点D是线段OC（不与点O、点C重合）上一动点，在线段OD的 ‎ ‎ 右侧作正方形ODEF,连接CE、BE，设线段OD=t，△CEB的面积为S，求S与t ‎ 的函数关系式，并写出自变量t的取值范围；‎ 答案：解： （1） A(1,0)、 …2分（写对一个给1分）；‎ ‎（2）m=1(或解析式)………3分 ‎ 当00时，>0‎ ‎ ∴抛物线顶点一定不在第四象限 …‎ ‎ 设顶点横坐标为m，纵坐标为n，则 ∵‎ ‎ ∴当时，n有最小值