【数学】2020届北京一轮复习通用版2-1函数的概念及表示

【数学】2020届北京一轮复习通用版2-1函数的概念及表示

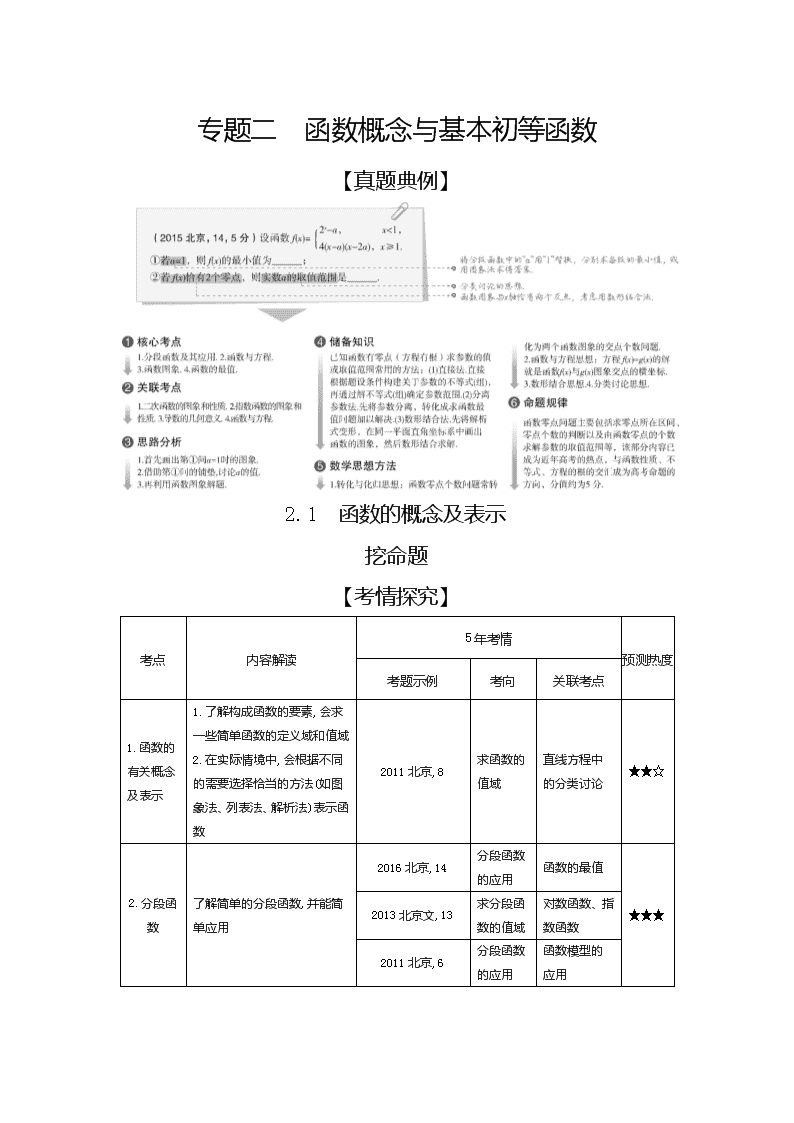
专题二　函数概念与基本初等函数 ‎【真题典例】‎ ‎2.1　函数的概念及表示 挖命题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 ‎1.函数的有关概念及表示 ‎1.了解构成函数的要素,会求一些简单函数的定义域和值域 ‎2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数 ‎2011北京,8‎ 求函数的值域 直线方程中的分类讨论 ‎★★☆‎ ‎2.分段函数 了解简单的分段函数,并能简单应用 ‎2016北京,14‎ 分段函数的应用 函数的最值 ‎★★★‎ ‎2013北京文,13‎ 求分段函数的值域 对数函数、指数函数 ‎2011北京,6‎ 分段函数的应用 函数模型的应用 分析解读　　1.理解函数的概念,应把重点放在构成它的三要素上,并会根据定义判断两个函数是不是同一个函数.2.掌握函数的三种表示方法,即图象法、列表法、解析法.3.掌握分段函数及其应用.在解决分段函数问题时,要注意分段函数是一个函数,而不是几个函数,并会求其值域.4.分段函数图象的作法是高考的热点.5.本节在高考中分值为5分左右,属于中低档题.‎ 破考点 ‎【考点集训】‎ 考点一　函数的有关概念及表示 ‎1.函数f(x)=‎2‎x‎-1‎的定义域为(　　)‎ A.[0,+∞)　　　　B.[1,+∞)　　　　C.(-∞,0]　　　　D.(-∞,1]‎ 答案　A　‎ ‎2.函数f(x)=xx-1‎的定义域为　　　　. ‎ 答案　{x|x≥0且x≠1}‎ 考点二　分段函数 ‎3.某市家庭煤气的使用量x(m3)和煤气费f(x)(元)满足关系式f(x)=C,0A.‎已知某家庭今年前三个月的煤气使用量和煤气费如下表:‎ 月份 使用量 煤气费 一月份 ‎4 m3‎ ‎4元 二月份 ‎25 m3‎ ‎14元 三月份 ‎35 m3‎ ‎19元 若四月份该家庭使用了20 m3的煤气,则煤气费为(　　)‎ A.11.5元　　　　B.11元　　　　C.10.5元　　　　D.10元 答案　A　‎ ‎4.若函数f(x)=‎2‎x‎,x≤0,‎log‎2‎x,x>0,‎则f‎1‎‎4‎=　　　　;方程f(-x)=‎1‎‎2‎的解是　　　　. ‎ 答案　-2;-‎2‎或1‎ 炼技法 ‎【方法集训】‎ 方法1　求函数定义域的方法 ‎1.已知函数f(2-x)=‎4-‎x‎2‎,则函数 f(x)的定义域为(　　)‎ A.[0,+∞)　　　　B.[0,16]　　　　C.[0,4]　　　　D.[0,2]‎ 答案　B　‎ ‎2.已知函数f(x)的定义域是[-1,2],则y=f(x)+f(-x)的定义域是(　　)‎ A.[-1,1]　　　　B.[-2,2]　　　　C.[-1,2]　　　　D.[-2,1]‎ 答案　A　‎ 方法2　确定函数解析式的方法 ‎3.甲、乙两地相距500 km,汽车从甲地匀速行驶到乙地,速度v不能超过120 km/h.已知汽车每小时的运输成本为‎9‎‎250‎v‎2‎‎+360‎元,则全程运输成本y与速度v的函数关系是y=　　　　　　　　　,当汽车的行驶速度为　　　　km/h时,全程运输成本最小. ‎ 答案　18v+‎180 000‎v(01,‎则满足f(f(a))=|2f(a)-1|的实数a的取值范围为　　　　　　　　. ‎ 答案　a≤1或a≥4‎ 过专题 ‎【五年高考】‎ A组　自主命题·北京卷题组 考点一　函数的有关概念及表示 ‎(2011北京,8,5分)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为(　　)‎ A.{9,10,11}　　　　B.{9,10,12}　　　　C.{9,11,12}　　　　D.{10,11,12}‎ 答案　C　‎ 考点二　分段函数 ‎1.(2011北京,6,5分)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为f(x)=cx‎,xa.‎ ‎①若a=0,则f(x)的最大值为　　　　; ‎ ‎②若f(x)无最大值,则实数a的取值范围是　　　　. ‎ 答案　①2　②(-∞,-1)‎ ‎3.(2013北京文,13,5分)函数f(x)=log‎1‎‎2‎x,　x≥1,‎‎2‎x‎,　　　　x<1‎的值域为　　　　　　　. ‎ 答案　(-∞,2)‎ B组　统一命题、省(区、市)卷题组 考点一　函数的有关概念及表示 ‎1.(2014江西,3,5分)已知函数f(x)=5|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=(　　)‎ A.1　　　　B.2　　　　C.3　　　　D.-1‎ 答案　A　‎ ‎2.(2018江苏,5,5分)函数f(x)=log‎2‎x-1‎的定义域为　　　　. ‎ 答案　[2,+∞)‎ 考点二　分段函数 ‎1.(2015课标Ⅱ,5,5分)设函数f(x)=‎1+log‎2‎(2-x),　x<1,‎‎2‎x-1‎‎,　　　　x≥1,‎则f(-2)+f(log212)=(　　)‎ A.3　　　　B.6　　　　C.9　　　　D.12‎ 答案　C　‎ ‎2.(2018浙江,15,6分)已知λ∈R,函数f(x)=x-4,　　x≥λ,‎x‎2‎‎-4x+3,　　　　x<λ.‎当λ=2时,不等式f(x)<0的解集是　　　　.若函数f(x)恰有2个零点,则λ的取值范围是　　　　　　　. ‎ 答案　(1,4);(1,3]∪(4,+∞)‎ ‎3.(2017课标Ⅲ,15,5分)设函数f(x)=x+1,x≤0,‎‎2‎x‎,x>0,‎则满足f(x)+f x-‎‎1‎‎2‎>1的x的取值范围是　　　　. ‎ 答案　‎‎-‎1‎‎4‎,+∞‎ ‎4.(2014课标Ⅰ,15,5分)设函数f(x)=ex-1‎‎,x<1,‎x‎1‎‎3‎‎,x≥1,‎则使得f(x)≤2成立的x的取值范围是　　　　. ‎ 答案　(-∞,8]‎ C组　教师专用题组 考点一　函数的有关概念及表示 ‎1.(2017山东,9,5分)设f(x)=x‎,00,‎‎0,x=0,‎‎-1,x<0.‎则(　　)‎ A.|x|=x|sgn x|　　　　B.|x|=xsgn|x|　　　　C.|x|=|x|sgn x　　　　D.|x|=xsgn x 答案　D　‎ ‎2.(2015山东,10,5分)设函数f(x)=‎3x-1,‎x<1,‎‎2‎x‎,‎x≥1.‎则满足f(f(a))=2f(a)的a的取值范围是(　　)‎ A.‎2‎‎3‎‎,1‎　　　　B.[0,1]　　　　C.‎2‎‎3‎‎,+∞‎　　　　D.[1,+∞)‎ 答案　C　‎ ‎3.(2014福建,7,5分)已知函数f(x)=x‎2‎‎+1,x>0,‎cosx,x≤0,‎则下列结论正确的是(　　)‎ A. f(x)是偶函数　　　　B. f(x)是增函数　　　　C. f(x)是周期函数　　　　D. f(x)的值域为[-1,+∞)‎ 答案　D　‎ ‎4.(2014上海,18,5分)设f(x)=‎(x-a‎)‎‎2‎,x≤0,‎x+‎1‎x+a,x>0.‎若f(0)是 f(x)的最小值,则a的取值范围为(　　)‎ A.[-1,2]　　　　B.[-1,0]　　　　C.[1,2]　　　　D.[0,2]‎ 答案　D　‎ ‎5.(2018江苏,9,5分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(-2,2]上,f(x)=cosπx‎2‎,0

查看更多