- 2021-05-21 发布 |
- 37.5 KB |
- 27页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版九年级数学上册第二十四章圆直线和圆的位置关系切线的判定与性质课件
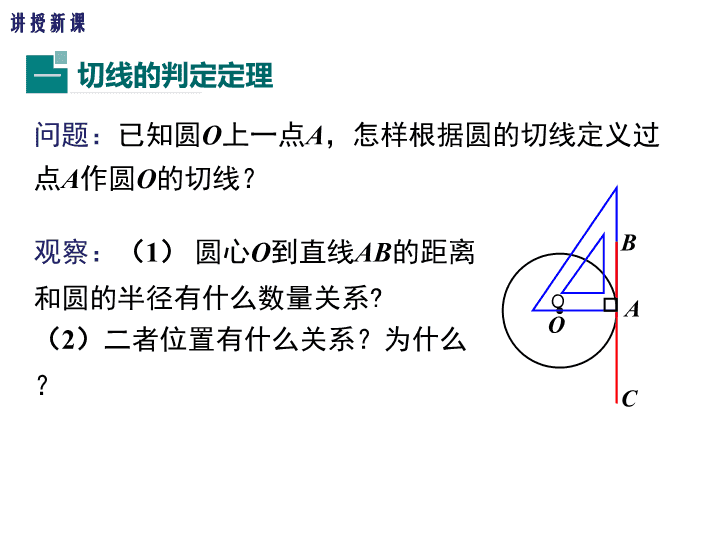
第二十四章 圆 人教版 九年级数学上册 切线的判定与性质 导入新课 情境引入 转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花, 都是沿着什么方向飞出的? 都是沿切线方向飞出的. 生活中常看到切线的实例,如何判断一条直线是 否为切线呢?学完这节课,你就都会明白. O A B C 问题:已知圆O上一点A,怎样根据圆的切线定义过 点A作圆O的切线? 观察:(1) 圆心O到直线AB的距离 和圆的半径有什么数量关系? (2)二者位置有什么关系?为什么? 切线的判定定理一 O 讲授新课 经过半径的外端并且垂直于这条 半径的直线是圆的切线. O A B C 切线的判定定理 应用格式 O 要点归纳 判一判:下列各直线是不是圆的切线?如果不是, 请说明为什么? O. l A O. l A B A O l (1) (2) (3) (1)不是,因为 没有垂直. (2),(3)不是,因为没有经过半径 的外端点A. 在此定理中,“经过半径的外端”和“垂直于这 条半径”,两个条件缺一不可,否则就不是圆的切线. 注意 判断一条直线是一个圆的切线有三个方法: 1.定义法:直线和圆只有一个 公共点时,我们说这条直线是 圆的切线; 2.数量关系法:圆心到这条 直线的距离等于半径(即d=r) 时,直线与圆相切; 3.判定定理:经过半径的外端且垂 直于这条半径的直线是圆的切线. l A l O l rd 要点归纳 例1:如图,∠ABC=45°,直线AB 是☉O上的直径,点A,且AB=AC. 求证:AC是☉O的切线. 解析:直线AC经过半径的一端,因此只要证OA垂直于AB即可. 证明:∵AB=AC,∠ABC=45°, ∴∠ACB=∠ABC=45°. ∴∠BAC=180°-∠ABC-ACB=90°. ∵AB是☉O的直径, ∴ AC是☉O的切线. A O C B 例2 已知:直线AB经过⊙ O上的点C,并且OA=OB, CA=CB.求证:直线AB是⊙ O的切线. 分析:由于AB过⊙ O上的点C,所以连接OC, 只要证明AB⊥OC即可. 证明:连接OC(如图). ∵ OA=OB,CA=CB, ∴ OC是等腰三角形OAB底边AB上的中线. ∴ AB⊥OC. ∵ OC是⊙ O的半径, ∴ AB是⊙ O的切线. 例3 如图,△ABC 中,AB =AC ,O 是BC的中点, ⊙ O 与AB 相切于E.求证:AC 是⊙ O 的切线. B O C E A分析:根据切线的判定定理, 要证明AC是⊙ O的切线,只要 证明由点O向AC所作的垂线段 OF是⊙ O的半径就可以了,而 OE是⊙ O的半径,因此只需要 证明OF=OE. F 证明:连接OE ,OA, 过O 作OF ⊥AC. ∵⊙ O 与AB 相切于E , ∴OE ⊥ AB. 又∵△ABC 中,AB =AC ,O 是BC 的中点. ∴AO 平分∠BAC, F B O C E A ∴OE =OF. ∵OE 是⊙ O 半径, OF =OE,OF ⊥ AC. ∴AC 是⊙ O 的切线. 又OE ⊥AB ,OF⊥AC. 如图,已知直线AB经过⊙ O上的 点C,并且OA=OB,CA=CB 求证:直线AB是⊙ O的切线. C BA O 如图,OA=OB=5,AB=8, ⊙ O的直径为6. 求证:直线AB是⊙ O的切线. C BA O 对比思考 作垂直连接 方法归纳 (1) 有交点,连半径,证垂直; (2) 无交点,作垂直,证半径. 证切线时辅助线的添加方法 例1 例2 有切线时常用辅助线添加方法 见切点,连半径,得垂直. 切线的其他重要结论 (1)经过圆心且垂直于切线的直线必经过切点; (2)经过切点且垂直于切线的直线必经过圆心. 要点归纳 思考:如图,如果直线l是⊙ O 的切线,点A为切点, 那么OA与l垂直吗? A l O ∵直线l是⊙ O 的切线,A是切点, ∴直线l ⊥OA. 切线的性质定理二 切线性质 圆的切线垂直于经过切点的半径. 应用格式 小亮的理由是:直径AB与直线CD要么垂直,要么不垂直. (1)假设AB与CD不垂直,过点O作一 条直径垂直于CD,垂足为M, (2)则OM查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档