2017中考数学压轴试题复习11 因动点产生的相似三角形问题含答案

2017中考数学压轴试题复习11 因动点产生的相似三角形问题含答案

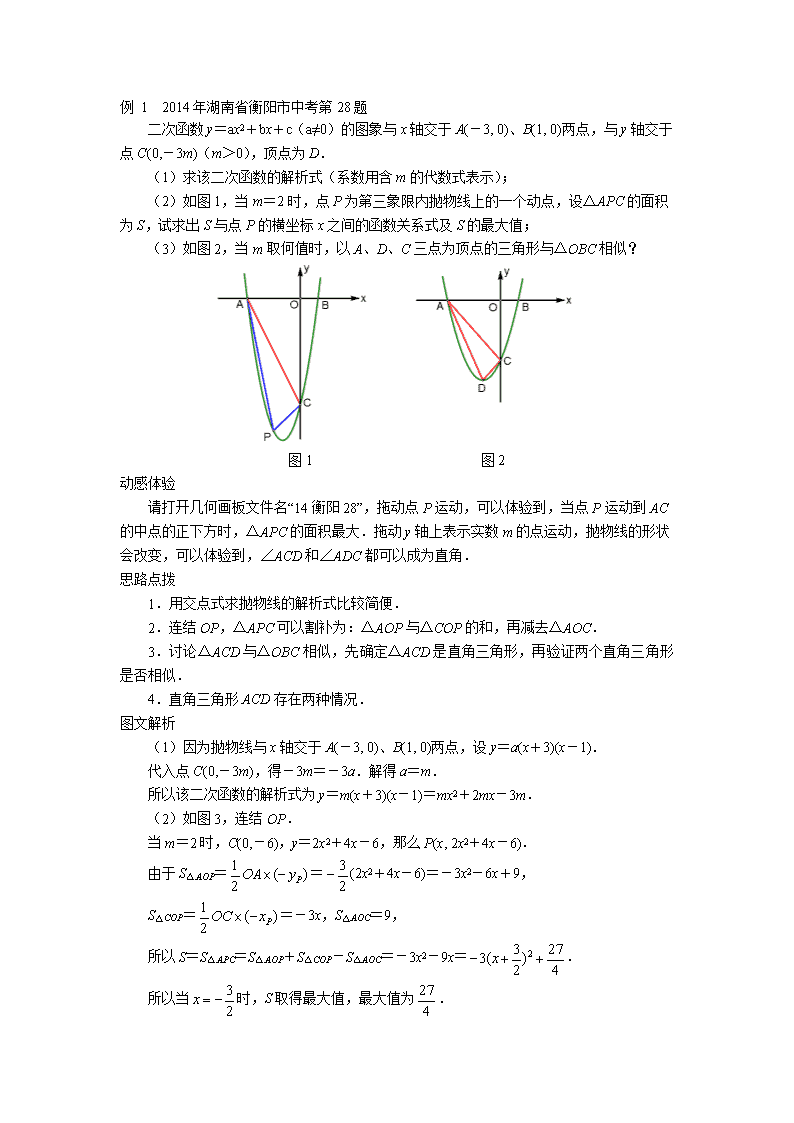
‎§1．1 因动点产生的相似三角形问题 课前导学 相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．‎ 判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．‎ 如果已知∠A＝∠D，探求△ABC与△DEF相似，只要把夹∠A和∠D的两边表示出来，按照对应边成比例，分和两种情况列方程．‎ 应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．‎ 应用判定定理3解题不多见，根据三边对应成比例列连比式解方程（组）．‎ 还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．‎ 求线段的长，要用到两点间的距离公式，而这个公式容易记错．理解记忆比较好．‎ 如图1，如果已知A、B两点的坐标，怎样求A、B两点间的距离呢？‎ 我们以AB为斜边构造直角三角形，直角边与坐标轴平行，这样用勾股定理就可以求斜边AB的长了．水平距离BC的长就是A、B两点间的水平距离，等于A、B两点的横坐标相减；竖直距离AC就是A、B两点间的竖直距离，等于A、B两点的纵坐标相减．‎ 图1‎ 例 1 2014年湖南省衡阳市中考第28题 二次函数y＝ax2＋bx＋c（a≠0）的图象与x轴交于A(－3, 0)、B(1, 0)两点，与y轴交于点C(0,－‎3m)（m＞0），顶点为D．‎ ‎（1）求该二次函数的解析式（系数用含m的代数式表示）；‎ ‎（2）如图1，当m＝2时，点P为第三象限内抛物线上的一个动点，设△APC的面积为S，试求出S与点P的横坐标x之间的函数关系式及S的最大值；‎ ‎（3）如图2，当m取何值时，以A、D、C三点为顶点的三角形与△OBC相似？‎ 图1 图2‎ 动感体验 请打开几何画板文件名“14衡阳28”，拖动点P运动，可以体验到，当点P运动到AC的中点的正下方时，△APC的面积最大．拖动y轴上表示实数m的点运动，抛物线的形状会改变，可以体验到，∠ACD和∠ADC都可以成为直角．‎ 思路点拨 ‎1．用交点式求抛物线的解析式比较简便．‎ ‎2．连结OP，△APC可以割补为：△AOP与△COP的和，再减去△AOC．‎ ‎3．讨论△ACD与△OBC相似，先确定△ACD是直角三角形，再验证两个直角三角形是否相似．‎ ‎4．直角三角形ACD存在两种情况．‎ 图文解析 ‎（1）因为抛物线与x轴交于A(－3, 0)、B(1, 0)两点，设y＝a(x＋3)(x－1)．‎ 代入点C(0,－‎3m)，得－‎3m＝－‎3a．解得a＝m．‎ 所以该二次函数的解析式为y＝m(x＋3)(x－1)＝mx2＋2mx－‎3m．‎ ‎（2）如图3，连结OP．‎ 当m＝2时，C(0,－6)，y＝2x2＋4x－6，那么P(x, 2x2＋4x－6)．‎ 由于S△AOP＝＝(2x2＋4x－6)＝－3x2－6x＋9， ‎ S△COP＝＝－3x，S△AOC＝9，‎ 所以S＝S△APC＝S△AOP＋S△COP－S△AOC＝－3x2－9x＝．‎ 所以当时，S取得最大值，最大值为．‎ 图3 图4 图5‎ ‎（3）如图4，过点D作y轴的垂线，垂足为E．过点A作x轴的垂线交DE于F．‎ 由y＝m(x＋3)(x－1)＝m(x＋1)2－‎4m，得D(－1,－‎4m)．‎ 在Rt△OBC中，OB∶OC＝1∶‎3m．‎ 如果△ADC与△OBC相似，那么△ADC是直角三角形，而且两条直角边的比为1∶‎3m．‎ ‎①如图4，当∠ACD＝90°时，．所以．解得m＝1．‎ 此时，．所以．所以△CDA∽△OBC．‎ ‎②如图5，当∠ADC＝90°时，．所以．解得．‎ 此时，而．因此△DCA与△OBC不相似．‎ 综上所述，当m＝1时，△CDA∽△OBC．‎ 考点伸展 第（2）题还可以这样割补：‎ 如图6，过点P作x轴的垂线与AC交于点H．‎ 由直线AC：y＝－2x－6，可得H(x,－2x－6)．‎ 又因为P(x, 2x2＋4x－6)，所以HP＝－2x2－6x．‎ 因为△PAH与△PCH有公共底边HP，高的和为A、C两点间的水平距离3，所以 S＝S△APC＝S△APH＋S△CPH ‎＝(－2x2－6x)‎ ‎＝． 图6‎ 例 2 2014年湖南省益阳市中考第21题 如图1，在直角梯形ABCD中，AB//CD，AD⊥AB，∠B＝60°，AB＝10，BC＝4，点P沿线段AB从点A向点B运动，设AP＝x．2·1·c·n·j·y ‎（1）求AD的长；‎ ‎（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；‎ ‎（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S＝S1＋S2，求S的最小值. ‎ 动感体验 图1‎ 请打开几何画板文件名“14益阳‎21”‎，拖动点P在AB上运动，可以体验到，圆心O的运动轨迹是线段BC的垂直平分线上的一条线段．观察S随点P运动的图象，可以看到，S有最小值，此时点P看上去象是AB的中点，其实离得很近而已．‎ 思路点拨 ‎1．第（2）题先确定△PCB是直角三角形，再验证两个三角形是否相似．‎ ‎2．第（3）题理解△PCB的外接圆的圆心O很关键，圆心O在确定的BC的垂直平分线上，同时又在不确定的BP的垂直平分线上．而BP与AP是相关的，这样就可以以AP为自变量，求S的函数关系式．‎ 图文解析 ‎（1）如图2，作CH⊥AB于H，那么AD＝CH．‎ 在Rt△BCH中，∠B＝60°，BC＝4，所以BH＝2，CH＝．所以AD＝．‎ ‎（2）因为△APD是直角三角形，如果△APD与△PCB相似，那么△PCB一定是直角三角形．‎ ‎①如图3，当∠CPB＝90°时，AP＝10－2＝8．‎ 所以＝＝，而＝．此时△APD与△PCB不相似．‎ 图2 图3 图4‎ ‎②如图4，当∠BCP＝90°时，BP＝2BC＝8．所以AP＝2．‎ 所以＝＝．所以∠APD＝60°．此时△APD∽△CBP．‎ 综上所述，当x＝2时，△APD∽△CBP．‎ ‎（3）如图5，设△ADP的外接圆的圆心为G，那么点G是斜边DP的中点．‎ 设△PCB的外接圆的圆心为O，那么点O在BC边的垂直平分线上，设这条直线与BC交于点E，与AB交于点F．‎ 设AP＝‎2m．作OM⊥BP于M，那么BM＝PM＝5－m．‎ 在Rt△BEF中，BE＝2，∠B＝60°，所以BF＝4．‎ 在Rt△OFM中，FM＝BF－BM＝4－(5－m)＝m－1，∠OFM＝30°，‎ 所以OM＝．‎ 所以OB2＝BM2＋OM2＝．‎ 在Rt△ADP中，DP2＝AD2＋AP2＝12＋‎4m2‎．所以GP2＝3＋m2．‎ 于是S＝S1＋S2＝π(GP2＋OB2)‎ ‎＝＝．‎ 所以当时，S取得最小值，最小值为．‎ 图5 图6‎ 考点伸展 关于第（3）题，我们再讨论个问题．‎ 问题1，为什么设AP＝‎2m呢？这是因为线段AB＝AP＋PM＋BM＝AP＋2BM＝10．‎ 这样BM＝5－m，后续可以减少一些分数运算．这不影响求S的最小值．‎ 问题2，如果圆心O在线段EF的延长线上，S关于m的解析式是什么？‎ 如图6，圆心O在线段EF的延长线上时，不同的是FM＝BM－BF＝(5－m)－4＝1－m．‎ 此时OB2＝BM2＋OM2＝．这并不影响S关于m的解析式．‎ 例 3 2015年湖南省湘西市中考第26题 如图1，已知直线y＝－x＋3与x轴、y轴分别交于A、B两点，抛物线y＝－x2＋bx＋c经过A、B两点，点P在线段OA上，从点O出发，向点A以每秒1个单位的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以每秒个单位的速度匀速运动，连结PQ，设运动时间为t秒．‎ ‎（1）求抛物线的解析式；‎ ‎（2）问：当t为何值时，△APQ为直角三角形；‎ ‎（3）过点P作PE//y轴，交AB于点E，过点Q作QF//y轴，交抛物线于点F，连结EF，当EF//PQ时，求点F的坐标；‎ ‎（4）设抛物线顶点为M，连结BP、BM、MQ，问：是否存在t的值，使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由． 图1‎ 动感体验 请打开几何画板文件名“15湘西‎26”‎，拖动点P在OA上运动，可以体验到，△APQ有两个时刻可以成为直角三角形，四边形EPQF有一个时刻可以成为平行四边形，△MBQ与△BOP有一次机会相似．‎ 思路点拨 ‎1．在△APQ中，∠A＝45°，夹∠A的两条边AP、AQ都可以用t表示，分两种情况讨论直角三角形APQ．‎ ‎2．先用含t的式子表示点P、Q的坐标，进而表示点E、F的坐标，根据PE＝QF列方程就好了．‎ ‎3．△MBQ与△BOP都是直角三角形，根据直角边对应成比例分两种情况讨论．‎ 图文解析 ‎（1）由y＝－x＋3，得A(3, 0)，B(0, 3)．‎ 将A(3, 0)、B(0, 3)分别代入y＝－x2＋bx＋c，得 解得 所以抛物线的解析式为y＝－x2＋2x＋3．‎ ‎（2）在△APQ中，∠PAQ＝45°，AP＝3－t，AQ＝t．‎ 分两种情况讨论直角三角形APQ：‎ ‎①当∠PQA＝90°时，AP＝AQ．解方程3－t＝2t，得t＝1（如图2）．‎ ‎②当∠QPA＝90°时，AQ＝AP．解方程t＝(3－t)，得t＝1.5（如图3）．‎ 图2 图3‎ ‎（3）如图4，因为PE//QF，当EF//PQ时，四边形EPQF是平行四边形．‎ 所以EP＝FQ．所以yE－yP＝yF－yQ．‎ 因为xP＝t，xQ＝3－t，所以yE＝3－t，yQ＝t，yF＝－(3－t)2＋2(3－t)＋3＝－t2＋4t．‎ 因为yE－yP＝yF－yQ，解方程3－t＝(－t2＋4t)－t，得t＝1，或t＝3（舍去）．所以点F的坐标为(2, 3)．‎ 图4 图5‎ ‎（4）由y＝－x2＋2x＋3＝－(x－1)2＋4，得M(1, 4)．‎ 由A(3, 0)、B(0, 3)，可知A、B两点间的水平距离、竖直距离相等，AB＝3．‎ 由B(0, 3)、M(1, 4)，可知B、M两点间的水平距离、竖直距离相等，BM＝．‎ 所以∠MBQ＝∠BOP＝90°．因此△MBQ与△BOP相似存在两种可能：‎ ‎①当时，．解得（如图5）．‎ ‎②当时，．整理，得t2－3t＋3＝0．此方程无实根．‎ 考点伸展 第（3）题也可以用坐标平移的方法：由P(t, 0)，E(t, 3－t)，Q(3－t, t)，按照P→E方向，将点Q向上平移，得F(3－t, 3)．再将F(3－t, 3)代入y＝－x2＋2x＋3，得t＝1，或t＝3．‎ ‎ ‎